regression and gradient descent

What can regression do?

• Stock Market Forecast
• Self-driving Car
• Recommendation

Step 1 : choose a set of functions (module choosing)

Linear module

Step 2 : Training Data

Pokemon features (height, weight, type …..) and cp(combat power) after evolution.

Step 3: Loss function

Loss function $ \mathrm{Loss}(f) = \mathrm{Loss}(arg1 , arg2 , ….)$ is a function receive a function as its input and gives how bad it is. It makes judgment of a group of arguments.

For example:
$$
J(\theta) = \frac{1}{2}\sum_{i=1}^n(h_{\theta}(x^{(i)})-y^{(i)})^2
$$

After you get the result : error evalutation

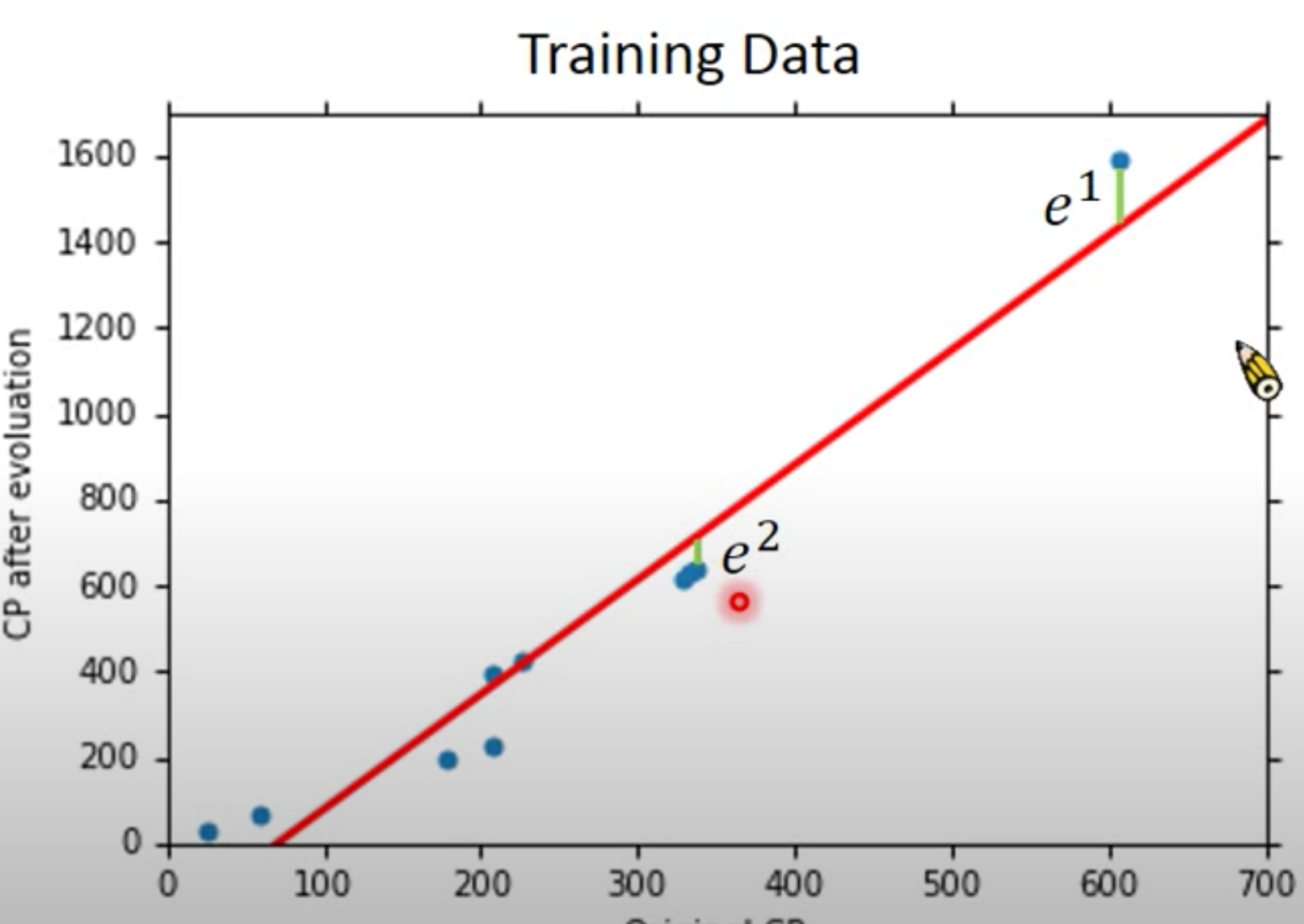
we should use another data set call Testing Data

then calculate the average error on new data
$$
\sum_{i=0}^ne^i
$$

How can you improve ?

choose another module
$$
y = b + w_1x_{cp} + w_2(x_{cp}^2)
$$
…

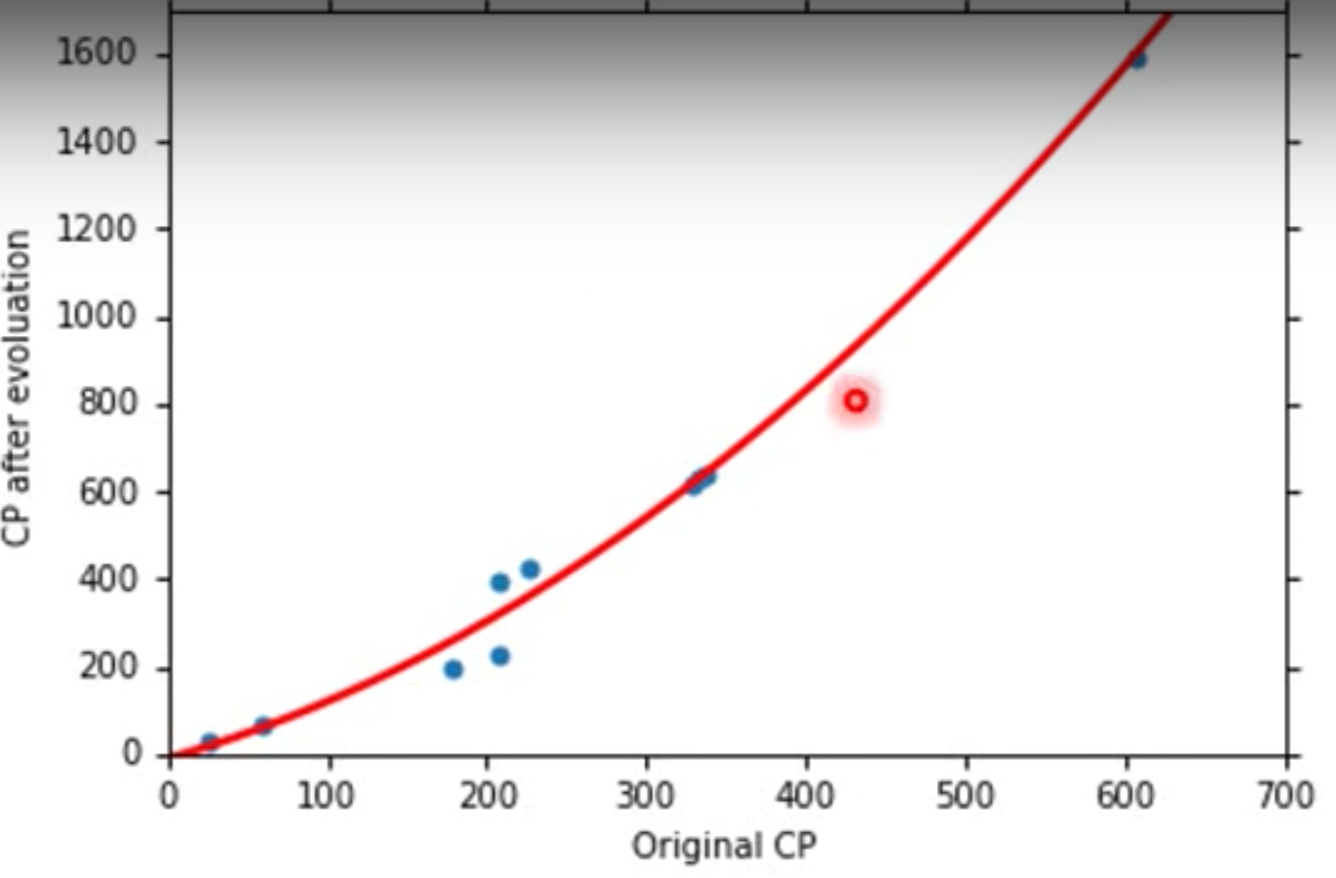
However, this kind of improvement is not reliable

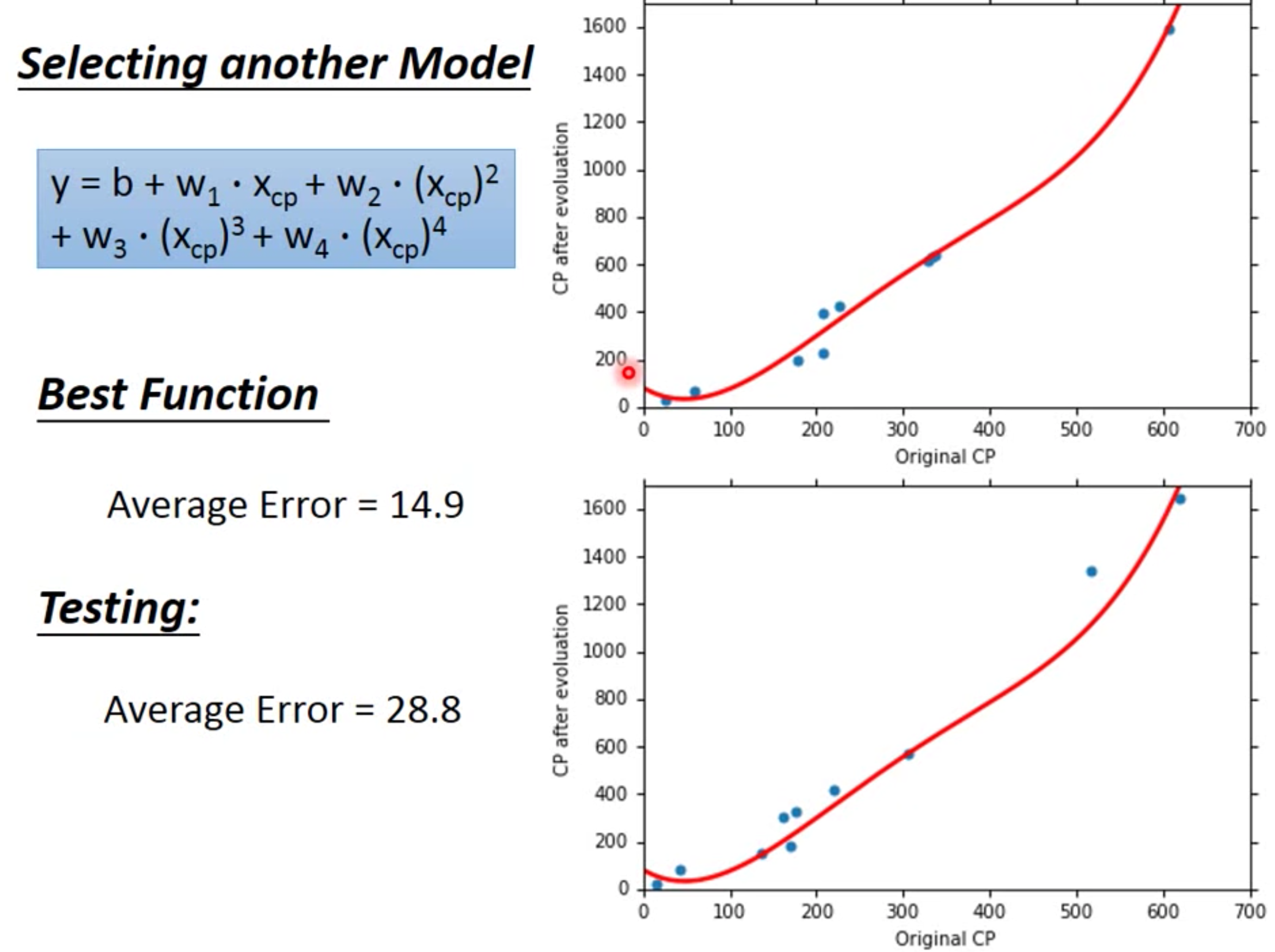
We can see that as the module become more and more complex, its performance on training data becomes better, but not the training data, lead to overfitting

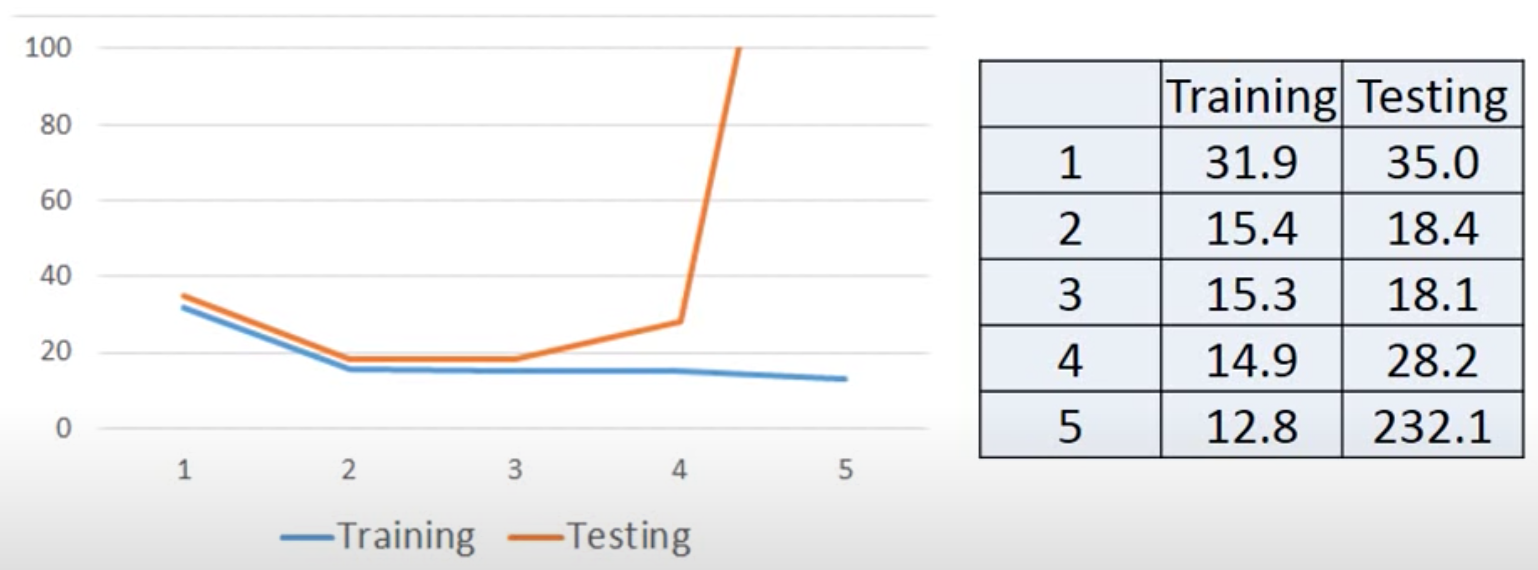
Let’s collect more data

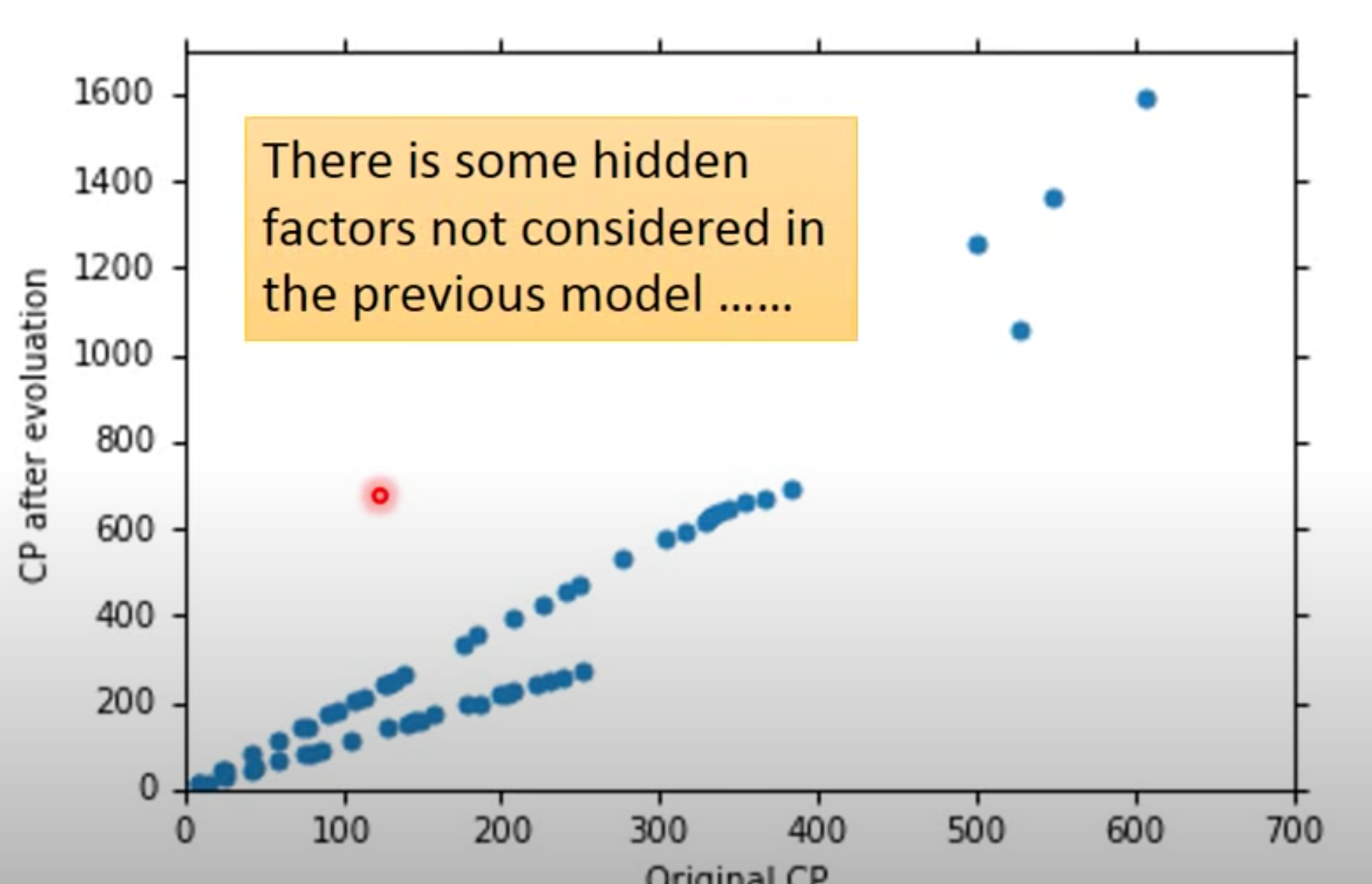
It turn out that there is an important factor, the type of Pokemon is ignored by the previous model. So it is very important to consider everything you can before choosing the module!!!

And we can still use linear module by adding the factor as a new feature.

Improve loss function via Regularization

• what is regularization?

  Regularization is a technique used in an attempt to solve the overfitting problem in statistical models.

we redefine our loss function as this(add $\lambda \sum (\theta_i)^2$ ):
$$
L = \sum_n(y-h_{\theta}(x))^2 + \lambda \sum (\theta_i)^2
$$
we can make the arguments be as close as possible to 0, make the function more smooth because smooth function are not that sensitive to input. (You may need to adjust the value of $\lambda$ manually)

• the deviation between y and h is considered less in new loss function.(inhibit overfitting)

• we prefer smooth, but don’t be too smooth, don’t make the $\lambda$ too big.(调参侠诞生了🦹‍♀️)

• why the const value in loss function, the $b$ is ignored?

  • because $b$ will not affact how smooth the loss function is.

---

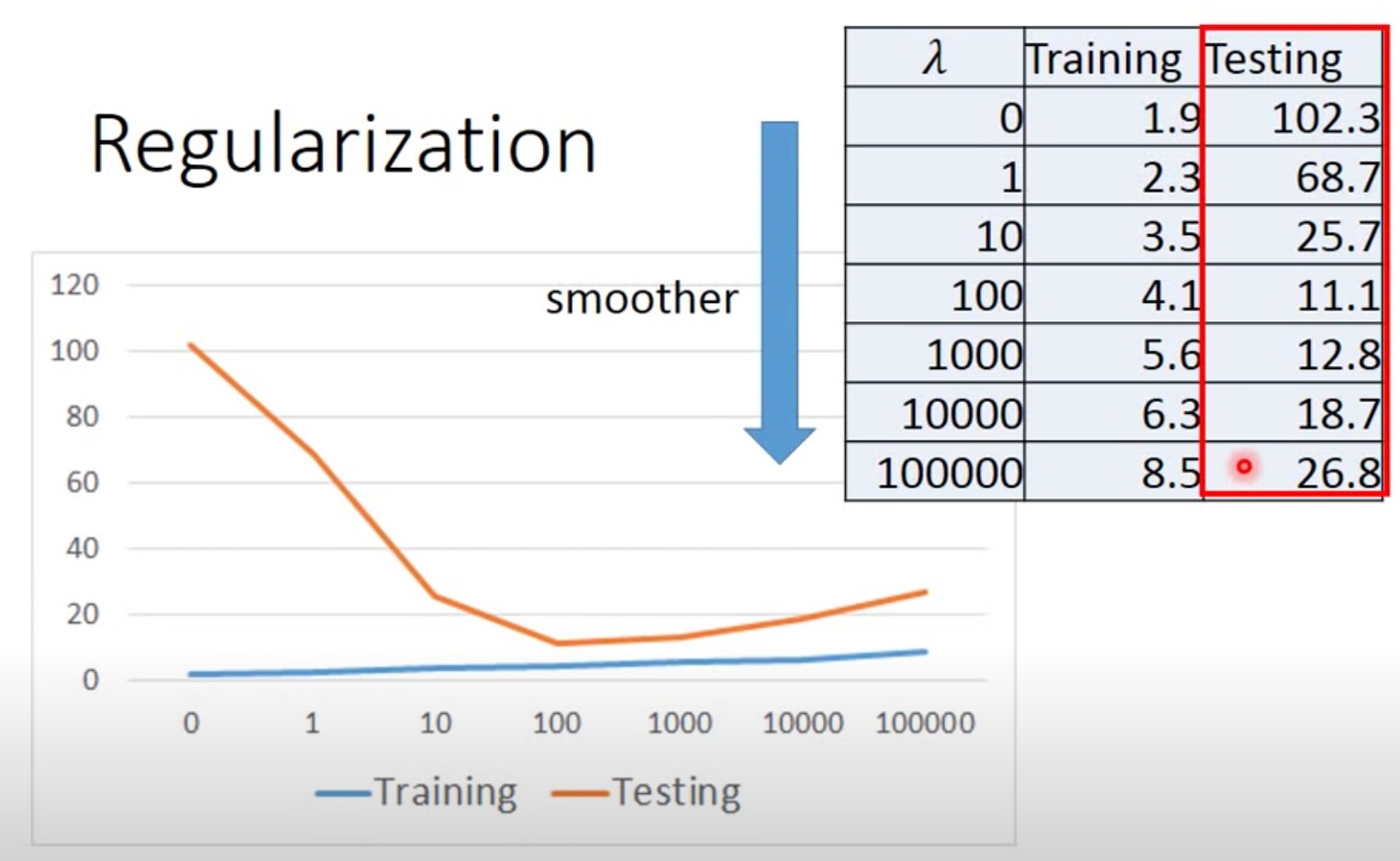
Let’s get some hand-on experience

Normal Equation

import numpy as np

# training set x,y
x = [338. , 333. , 328. , 207. , 226. ,25. , 179. , 60. , 208. , 606. ]
y = [640. , 633. , 619. , 393. , 428. ,27. , 193. , 66. , 226. , 1591.]

# hypothesis : y = a0 * 1 + a1 * x1

X = np.array([np.array([1,i])  for i in x]) # 10 * 2

Y = np.array(y).reshape(len(y) , 1) # 10 * 1

parameters = np.linalg.inv( X.T.dot(X)).dot(X.T).dot(Y) # 
print(parameters)

Gradient Descent

import numpy as np
import math as m

# training set x,y
x = [338. , 333. , 328. , 207. , 226. ,25. , 179. , 60. , 208. , 606. ]
y = [640. , 633. , 619. , 393. , 428. ,27. , 193. , 66. , 226. , 1591.]

# hypothesis : y = a0 * 1 + a1 * x1
# initialize arguments
a0 = -120.
a1 = -4.
parameters = np.array([a0 , a1]).reshape(1,2)

# respective learning rate for each parameter
p1rate =0.0
p2rate =0.0

iteration = 100000

# partial derivative of a_i : 2.0 * (y_i - hypothesis_i )*x_i
for step in range(iteration):
    
    sum1 = 0
    sum2 = 0
    
    # use all examples in training set
    for n in range(len(x)):
        temp = y[n]-np.dot(parameters,np.array([1,x[n]]).reshape(2,1))[0][0]
        sum1  -=  2.0  * ( temp  * 1.0 )
        sum2  -=  2.0  * ( temp  * x[n])

    # update learning rate
    p1rate += sum1**2
    p2rate += sum2**2

    # update parameters
    parameters[0][0] -= 1/m.sqrt(p1rate) * sum1
    parameters[0][1] -= 1/m.sqrt(p2rate) * sum2

# result
print(parameters)