2021-06-01

Data Structure

Sort

Some sorting algorithm

Sorting Algorithm

Motivation

why we need sorting?

Problems become easy once items become sorted, e.g. finding a medium
Data compression
Computer Graphic
….

Bubble sort

Idea : floating the “bubble” to top via comparision&swaping in each round

it is only for educational purpose, don’t use it in real world.
time complexity is $O(n^2)$

Implementation

void bubblesort(int * array , size_t size){
    for (int i = 0 ; i < size ; i++){	//O(n)
        for (int j = 0 ; j + 1 < size ; j++){	//O(n)
            if(array[j] < array[j+1])
                swap(&array[j] , &array[j+1]);
        }
    }
}

The bubble sort algorithm can be optimized by observing that the n-th round finds the n-th largest element and puts it into its final place. So, the inner loop can avoid looking at the last n − 1 items when running for the n-th time:
Also, if n-1 elements are already in the right position, the left 1 must be in the right position, too.

void bubblesort(int * array , size_t size){
    for (int i = 0 ; i < size - 1  ; i++){
        for (int j = 0 ; j + 1 < size - i ; j++){
            if(array[j] < array[j+1])
                swap(&array[j] , &array[j+1]);
        }
    }
}

Insertion sort

Idea : assume we have an empty sorted array, then float elements into right position in the array via swaping&comparision

time complexity(worst case) : $T = O(1+2+3+..+n) = O(n^2)$
we might obtain $O(n\log n)$ complexity by finding the right place via binary search first, then insert it directly. However, shifting an array need time, linked list do not support binary search, the idea is not practical.

Implementation

void insertion_sort(int * array , size_t size){
    for (int i = 0 ; i < size ; i ++ ){
        for (int j = i ; j - 1 >= 0 ; j--){
            if (array[j-1] < array[j])
                swap(&array[j] , &array[j-1]);
        }
    }
}

we can also start from i=1(start with a sorted one element array instead of an empty one.) and do the shifting.

void insertion_sort(int * array , size_t size){
    for (int i = 1 ; i < size ; i ++ ){
        int j = i;
        int key = array[i];
        for ( ; j - 1 >= 0  && array[j-1] < key; j--){
            array[j] = array[j-1];	//shift elements
        }
        array[j] = key;	//insert to the right position
    }
}

Merge sort

*Idea : divide and conquer, recurisively merging**
Merge sort is not an in-place sort, it needs $O(n)$ auxiliary space
There exists an in-place merge sort, but the performence is not quite well in practice
Time complexity : $T (n) = 2T(\frac{n}{2}) + \underbrace{O(1)}_\text{split time} + c\cdot\underbrace{O(n)}_\text{merge time}$
$$
T(n) = n\log n
$$
We can use a recursion tree to solve recursion like this.

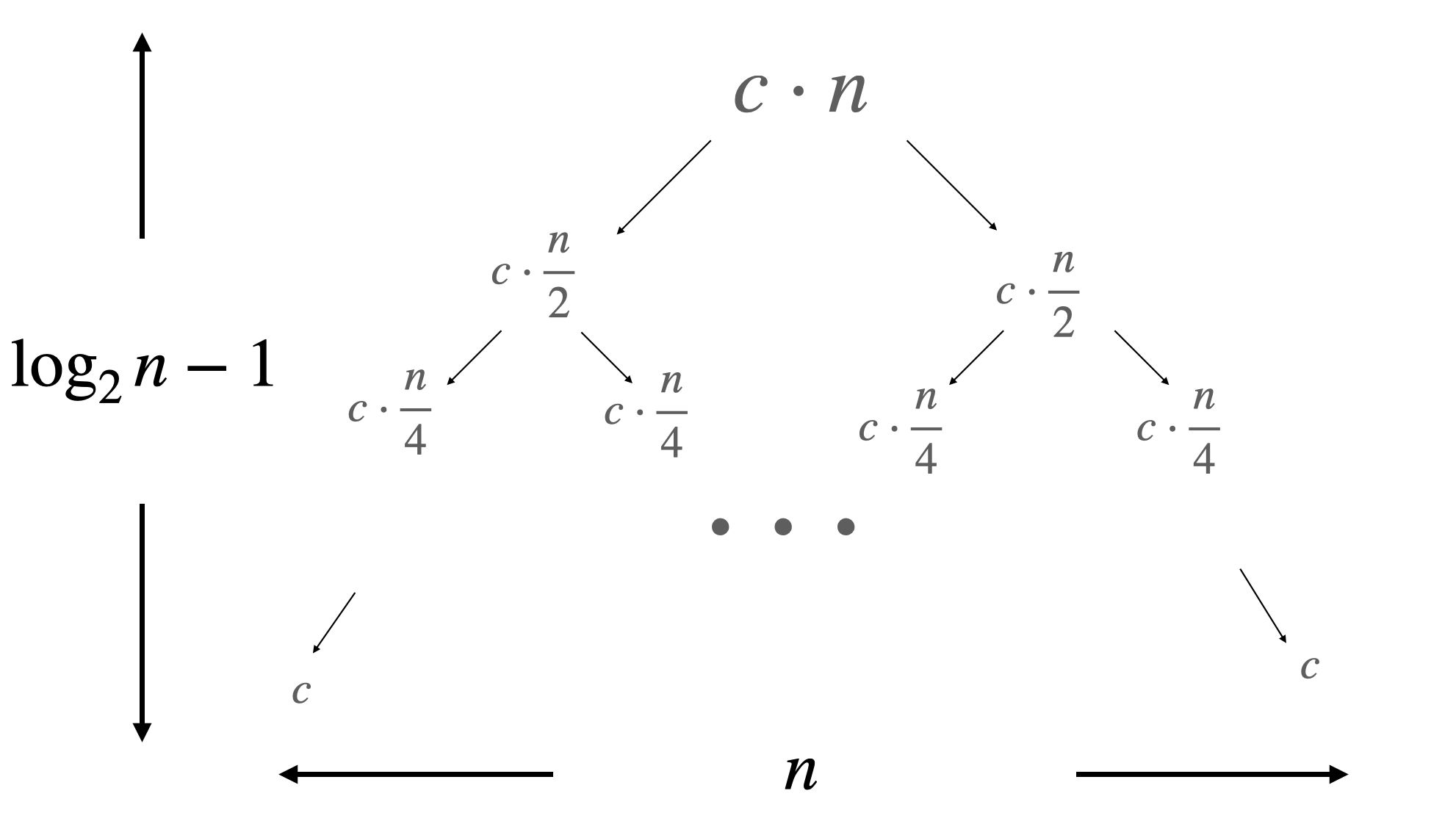
the total cost time is sum of sum of each level, or in other words, the sum of all the nodes.
$$
\sum c\cdot n + (c\cdot\frac{n}{2} + c\cdot\frac{n}{2}) + …+n\cdot c = [(\log_2n)-1]c\cdot n = O(n \log n)
$$

Implementation

void mymerge(int * array , int start , int mid , int end ){
    int head1 = start ;
    int head2 = mid+1 ;
    int size = end - start + 1;
    int auxiliary [size]; //this can be replaced by malloc
    int ptr = 0;
    while(head1 <= mid && head2 <= end){
        if(array[head1] < array[head2]){
            auxiliary[ptr++] = array[head1++];
        }
        else{
            auxiliary[ptr++] = array[head2++];
        }
    }
    //concatenate the rest
    int head = 0;
    int final = 0;
    if (head1 <= mid){
        head = head1;
        final = mid;
    }
    else{
        head = head2;
        final  = end;
    }
    for (int i = head ; i <= final ; i++){
        auxiliary[ptr++] = array[i];
    }
    
	//override the original array
    for(int j = 0; j < size ; j++){
        array[start++] = auxiliary[j];
    }

}

void mymergesort(int * array , int start , int  end ){
    if (end - start == 0) return ; //recursion base, there is only one element in array.
    int mid = (start + end) / 2;
    mymergesort(array , start , mid);
    mymergesort(array , mid + 1 , end);
    mymerge(array , start , mid , end);
}

void Mergesort(int * array , size_t size ){
    mymergesort(array , 0 , size-1);
}

Note that the auxiliary array is used for merging.

Quick sort

Idea : divide and conquer , recursively partition

Quick Sort | Brilliant Math & Science Wiki

This is an in-place sort
very practical
How:
1. Divide:
  
  Partition the array into 2 subarray around a pivot such that
2. Conquer:
  
  recursively sort the left of pivot and the right of the pivot
The key part of the algorithm is the partitioning
- we arbitrarily pick up an element and make it pivot, for example the most left one.

//we can start with
int pivot = a[0];
int i = 1;
int j = 2;
if (a[j+1] > pivot) j++;
else swap(&a[++j] , &a[++i]);

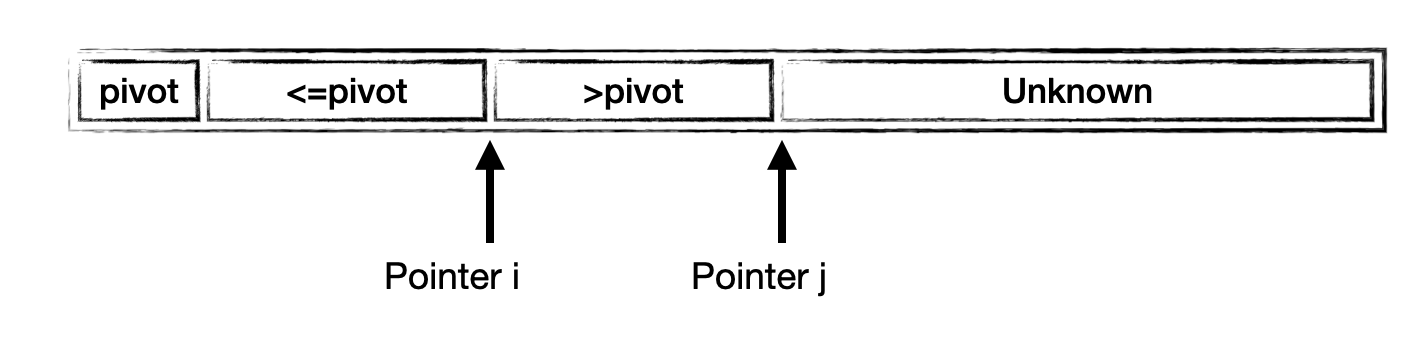
partition

the standard version
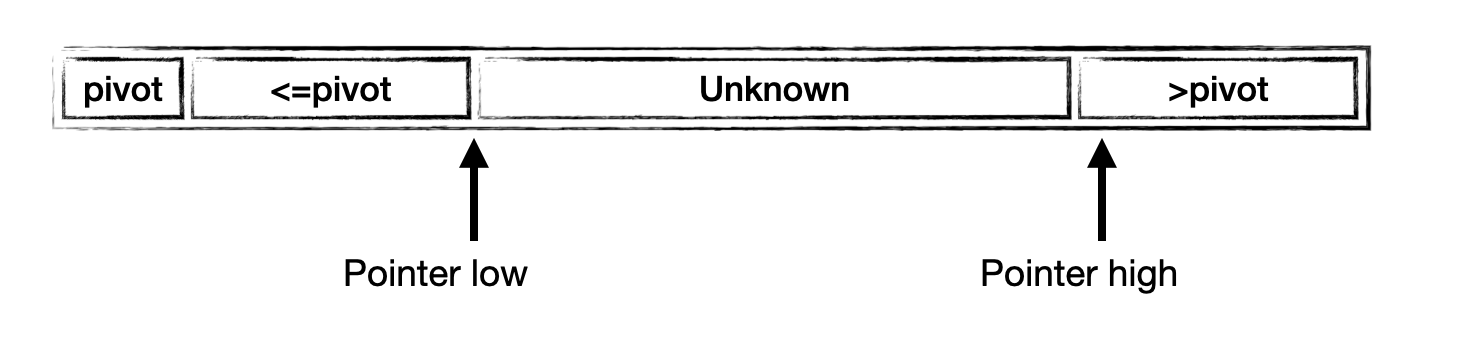
When we run out of the unknow part, we swap the pivot to the middle
1
swap(&a[0] , &a[i]);
Then recursively sort the left and right, don’t forget to return i, we need to pass the position to recursion.
In the worst case(the input array is already sorted), the complexity will be $O(n^2)$
In the best case(we partition at the middle every time), the complexity will be $O(n \log n)$
If we partition at $\frac{1}{10},\frac{9}{10}$ at each time, we still get $O(n \log n )$(verify this by using a recursion tree)
In order to be “lucky”$O(n \log n)$ most of the time, we can choose the pivot randomly to avoid sorting a sorted array.

Randomized Quicksort

the complexity is independent of the input, it is always $O(n \log n)$
the worst case will only appear if our RNG gives a “bad” random number.

Implementation

int partition(int * array , int start , int end){
    int pivot = array[start];
    int i = start ;
    int j = start + 1 ;
    while( j  <= end){
        if (array[j] <= pivot)  swap(&array[++i] , &array[j]);
        j++;
    }
    swap(&array[start], &array[i]);
    return i;
}

void quicksort(int * array , int start , int end ){
    if (end - start <= 0 ) return ;
    int position = partition(array , start , end);
    quicksort(array , start , position-1);
    quicksort(array , position+1 , end);
}

void Quicksort(int * array , size_t size){
    quicksort(array , 0 , size - 1);
}

Selection sort

Idea : The algorithm proceeds by finding the smallest/largest element in the unsorted sublist, swapping it into the right place and moving the sublist boundaries one element to the right.

time complexity : $O(n^2)$
in-place sort
generally performs worse than the similar insertion sort

Implementation

void selectionsort(int * array , size_t size){
    for (int i = 0 ; i < size ; i++){
        int smallest = i;
        for ( int j = i ; j < size ; j++){
            if (array[smallest] > array[j]){
                smallest = j;
            }
        }
        if(i!=smallest){
            swap(&array[smallest] , &array[i]);
        }
    }
}

Shell sort

Idea : take elements at certain interval as a subarray, use input sensitive sorting alogrithm(for example, insertion sort) to sort it, and then repeat the operation with a smaller interval. Finally reduce the interval to 1.

Repeatedly do insertion sort on all elements at fixed, decreasing distances apart: hk, hk-1, ..., h1= 1. The fact that the last increment used should be 1 means that regular insertion sort is done at the last step, guaranteeing that the array will be sorted.

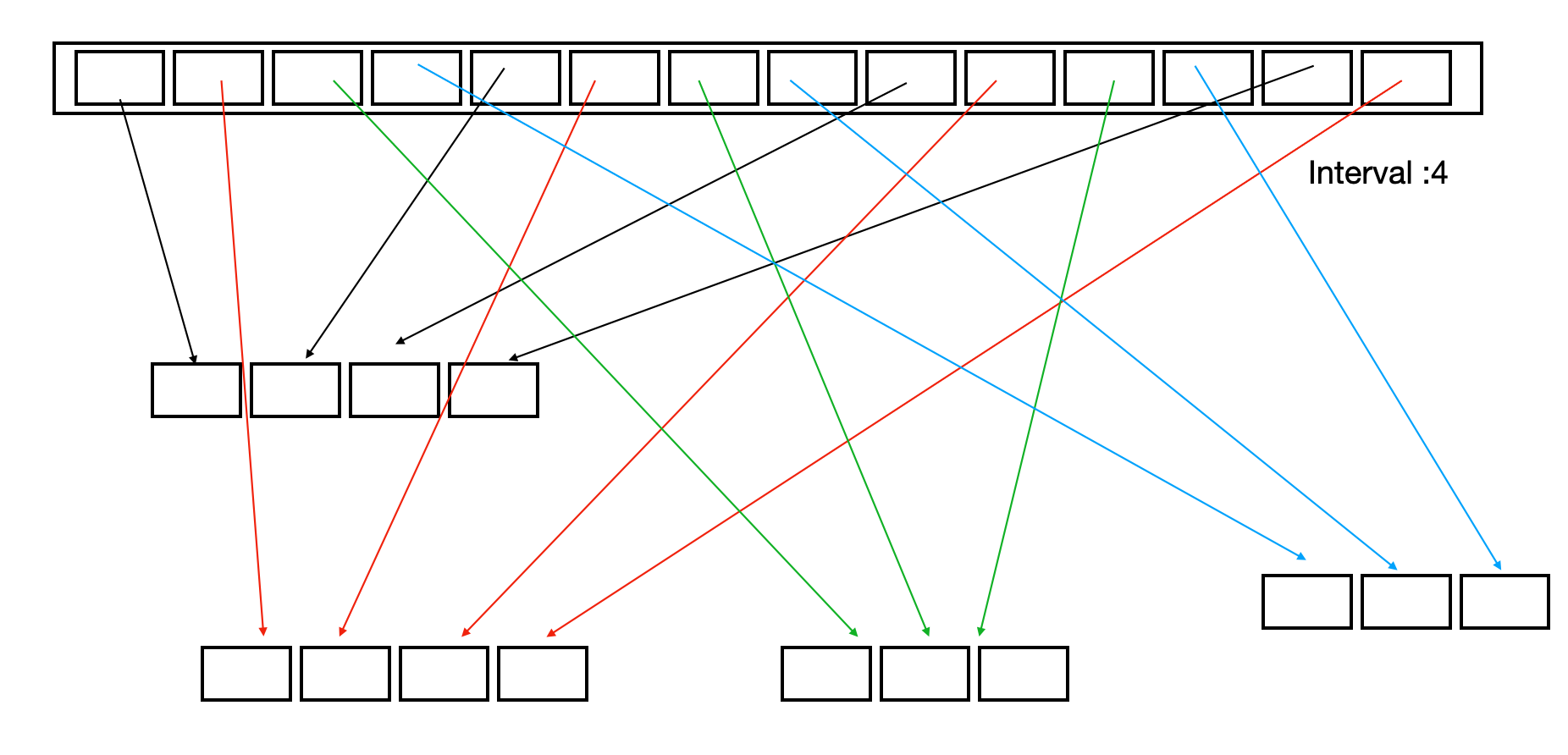
interval

in-place sort
time complexity is influenced by the “gap/interval sequence”,

find k0 so that 2k0 - 1 < size
for (k = k0; k > 0; --k) {  // from larger increments to smaller
  inc = 2k- 1;              // get array increment
  for (i = 0; i < inc; ++i) {
    insertionSort( [ a[i], a[i+inc], a[i+2*inc], ... ] );
  }
}

Implementation

void shellsort(int * array , size_t size){
    const int gapnum = 3;	
    int gaps [gapnum] = {4,2,1};	//gap sequence
    for (int i = 0 ; i < gapnum ; i++ ){
        int gap = gaps[i];
        //insertion sort for each gap
        //be careful when increase/decrease the index, do not access beyond the boundary
        for (int j = 0 ; j + gap < size ; j += gap){
        for (int k = j ; k >= 0 && array[k] < array[k+gap] ; k-=gap){
               swap(&array[k] , &array[k+gap]);
           }
        }
    }
}

summary