Floating Point & IEEE 754
Some real numbers can never be represent in binary precisely
$$
\frac{1}{10} , \frac{1}{3},\frac{1}{5} ,…
$$
With a limited number of bits, we have to make a trade-off between range and precision
Why not use 2’s complement to encode exponent part?
We can’t compare two 2’s complement encoded number directly, but we can do the same to $Exp - \text{bias}$ encoded number to get a true comparison
Why we have the bias?
we want to have a monotonic range to ease our comparison
$$
[-127 , 128] +\text{bias} = [0,128 + \text{bias}]
$$
Halfway in binary
always in the form of x.xxxxx1000000….
“Half way” when bits to right of rounding position = $(100…)_2$
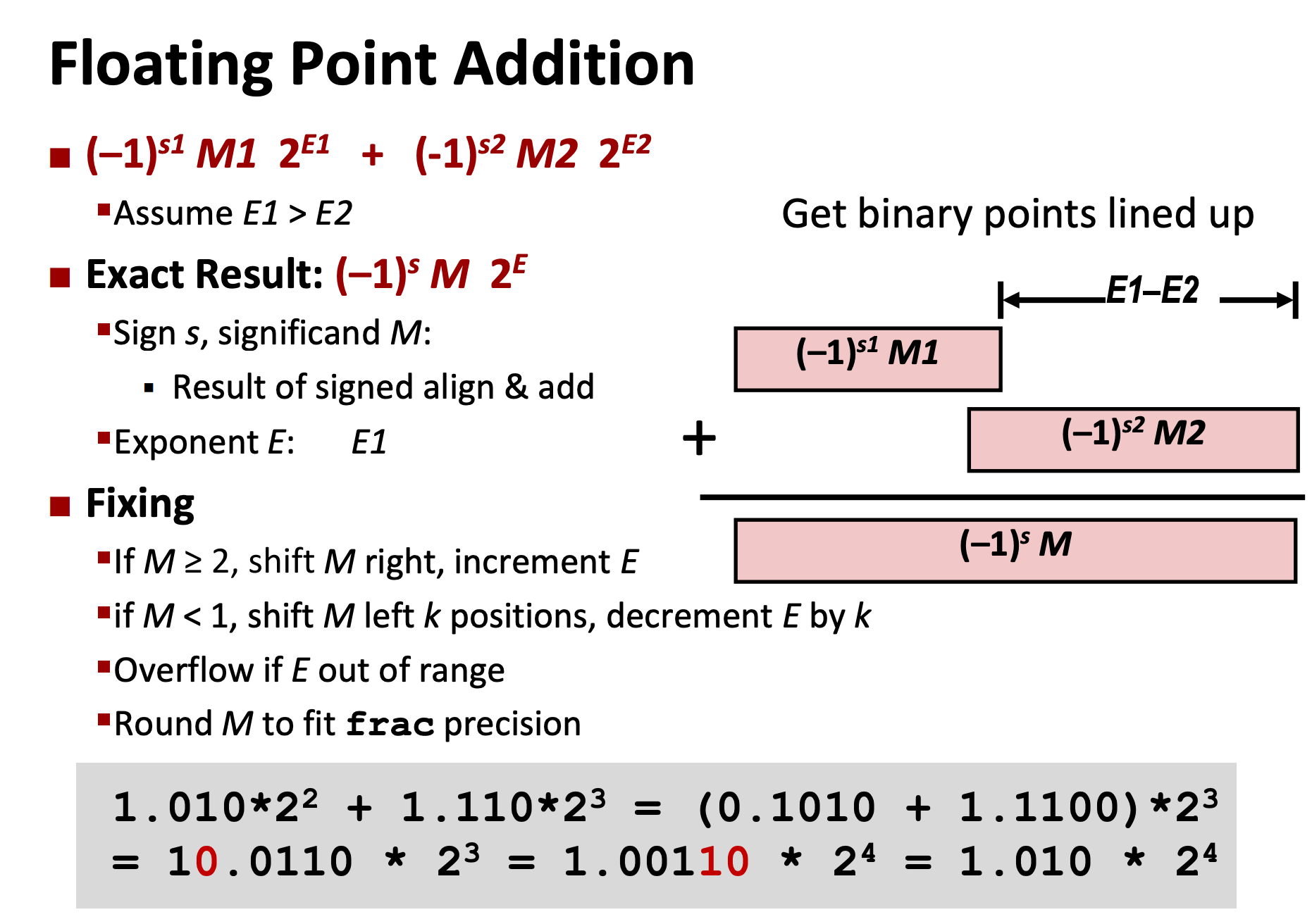
Float Point arithmetic

Casting in C
when doing casting, we examinate the fraction part of float point to see whether we need to round or not.