csapp

Ch3

Machine-Level Representation of Programs

In this chapter, we will take a close look at machine code and its human-readable representation as assembly code.

Best of all, a program written in a high-level language can be compiled and executed on a number of different machines, whereas assembly code is highly machine specific.

Our presentation is based on x86-64, the machine language for most of the processors found in today’s laptop and desktop machines, as well as those that power very large data centers and supercomputers.

3.1 A Historical Perspective

The Intel processor line, colloquially referred to as x86, has followed a long evolutionary development.

  • It started with one of the first single-chip 16-bit microprocessors, where many compromises had to be made due to the limited capabilities of integrated circuit technology at the time.

  • Since then, it has grown to take advantage of technology improvements as well as to satisfy the demands for higher performance and for supporting more advanced operating systems.

    • 8086 (1978, 29 K transistors).

      One of the first single-chip, 16-bit microprocessors. The 8088, a variant of the 8086 with an 8-bit external bus, formed the heart of the original IBM personal computers. IBM contracted with then-tiny Microsoft to develop the MS-DOS operating system. The original models came with 32,768 bytes of memory and two floppy drives (no hard drive). Architecturally, the machines were limited to a 655,360-byte address space—addresses were only 20 bits long (1,048,576 bytes addressable), and the operating system reserved 393,216 bytes for its own use. In 1980, Intel introduced the 8087 floating-point coprocessor (45 K transistors) to operate alongside an 8086 or 8088 processor, executing the floating-point instructions. The 8087 established the floating-point model for the x86 line, often referred to as “x87.”

    • 80286 (1982, 134 K transistors).

      Added more (and now obsolete) addressing modes. Formed the basis of the IBM PC-AT personal computer, the original platform for MS Windows.

    • i386 (1985, 275 K transistors).

      Expanded the architecture to 32 bits. Added the flat addressing model used by Linux and recent versions of the Windows operating system. This was the first machine in the series that could fully support a Unix operating system

    • i486 (1989, 1.2 M transistors).

      Improved performance and integrated the floating-point unit onto the processor chip but did not significantly change the instruction set.

    • Pentium (1993, 3.1 M transistors).

      Improved performance but only added minor extensions to the instruction set.

    • PentiumPro (1995, 5.5 M transistors).

      Introduced a radically new processor design, internally known as the P6 microarchitecture. Added a class of “conditional move” instructions to the instruction set.

    • Pentium/MMX (1997, 4.5 M transistors).

      Added new class of instructions to the Pentium processor for manipulating vectors of integers. Each datum can be 1, 2, or 4 bytes long. Each vector totals 64 bits.

    • Pentium II (1997, 7 M transistors).

      Continuation of the P6 microarchitecture.

    • Pentium III (1999, 8.2 M transistors).

      Introduced SSE, a class of instructions for manipulating vectors of integer or floating-point data. Each datum can be 1, 2, or 4 bytes, packed into vectors of 128 bits. Later versions of this chip went up to 24 M transistors, due to the incorporation of the level-2 cache on chip.

    • Pentium 4 (2000, 42 M transistors).

      Extended SSE to SSE2, adding new data types (including double-precision floating point), along with 144 new instructions for these formats. With these extensions, compilers can use SSE instructions, rather than x87 instructions, to compile floating-point code

    • Pentium 4E (2004, 125 M transistors).

      Added hyperthreading, a method to run two programs simultaneously on a single processor, as well as EM64T, Intel’s implementation of a 64-bit extension to IA32 developed by Advanced Micro Devices (AMD), which we refer to as x86-64.

    • Core 2 (2006, 291 M transistors).

      Returned to a microarchitecture similar to P6. First multi-core Intel microprocessor, where multiple processors are implemented on a single chip. Did not support hyperthreading.

    • Core i7, Nehalem (2008, 781 M transistors).

      Incorporated both hyperthreading and multi-core, with the initial version supporting two executing programs on each core and up to four cores on each chip.

    • Core i7, Sandy Bridge (2011, 1.17 G transistors).

      Introduced AVX, an extension of the SSE to support data packed into 256-bit vectors.

    • Core i7, Haswell (2013, 1.4 G transistors).

      Extended AVX to AVX2, adding more instructions and instruction formats.

  • Each successive processor has been designed to be backward compatible— able to run code compiled for any earlier version.

  • Intel has had several names for their processor line, including IA32, for “Intel Architecture 32-bit” and most recently Intel64, the 64-bit extension to IA32, which we will refer to as x86-64.

  • The memory model provided in the original 8086 and its extensions in the 80286 became obsolete with the i386. The original x87 floating-point instructions became obsolete with the introduction of SSE2.

3.2 Program Encodings

Suppose we write a C program as two files p1.c and p2.c. We can then compile this code using a Unix command line:

1
linux> gcc -Og -o p p1.c p2.c
  • The command-line option -Og instructs the compiler to apply a level of optimization that yields machine code that follows the overall structure of the original C code.
  • Invoking higher levels of optimization can generate code that is so heavily transformed that the relationship between the generated machine code and the original source code is difficult to understand.
  • We will therefore use -Og optimization as a learning tool and then see what happens as we increase the level of optimization. In practice, higher levels of optimization (e.g., specified with the option -O1 or -O2) are considered a better choice in terms of the resulting program performance.

3.2.1 Machine-Level Code

In the abstract model of computer, two of these are especially important for machine-level programming.

  • First, the format and behavior of a machine-level program is defined by the instruction set architecture, or ISA, defining the processor state, the format of the instructions, and the effect each of these instructions will have on the state.
  • Second, the memory addresses used by a machine-level program are virtual addresses, providing a memory model that appears to be a very large byte array

Being able to understand assembly code and how it relates to the original C code is a key step in understanding how computers execute programs.

The machine code for x86-64 differs greatly from the original C code. Parts of the processor state are visible that normally are hidden from the C programmer:

  • The program counter (commonly referred to as the PC, and called %rip in x86- 64) indicates the address in memory of the next instruction to be executed.

  • The integer register file contains 16 named locations storing 64-bit values.

    These registers can hold addresses (corresponding to C pointers) or integer data. Some registers are used to keep track of critical parts of the program state, while others are used to hold temporary data, such as the arguments and local variables of a procedure, as well as the value to be returned by a function.

  • The condition code registers hold status information about the most recently executed arithmetic or logical instruction.

    These are used to implement conditional changes in the control or data flow, such as is required to implement if and while statements.

  • A set of vector registers can each hold one or more integer or floating-point values.

Whereas C provides a model in which objects of different data types can be declared and allocated in memory, machine code views the memory as simply a large byte-addressable array

Aggregate data types in C such as arrays and structures are represented in machine code as contiguous collections of bytes.

Even for scalar data types, assembly code makes no distinctions between signed or unsigned integers, between different types of pointers, or even between pointers and integers.

(No “type” here !)

As mentioned earlier, the program memory is addressed using virtual addresses.

At any given time, only limited subranges of virtual addresses are considered valid.

For example, x86-64 virtual addresses are represented by 64-bit words. In current implementations of these machines, the upper 16 bits must be set to zero, and so an address can potentially specify a byte over a range of $2^{48}$, or 64 terabytes.

The operating system manages this virtual address space, translating virtual addresses into the physical addresses of values in the actual processor memory.

The compiler must generate sequences of instructions to implement program constructs such as arithmetic expression evaluation, loops, or procedure calls and returns.

The opensource community supporting gcc keeps changing the code generator, attempting to generate more efficient code according to changing code guidelines provided by the microprocessor manufacturers.

Our goal in studying the examples shown in our presentation is to demonstrate how to examine assembly code and map it back to the constructs found in high-level programming languages. You will need to adapt these techniques to the style of code generated by your particular compiler.

3.2.2 Code Examples

Suppose we write a C code file mstore.c containing the following function definition:

1
2
3
4
5
long mult2(long, long);
void multstore(long x, long y, long *dest) {
long t = mult2(x, y);
*dest = t;
}

To see the assembly code generated by the C compiler

1
$ gcc -Og -S mstore.c

-S will cause gcc to run the compiler, generating an assembly file mstore.s, and go no further.

The assembly-code file contains various declarations, including the following set of lines:

1
2
3
4
5
6
7
multstore:
	pushq	%rbx
	movq	%rdx, %rbx
	call	mult2@PLT
	movq	%rax, (%rbx)
	popq	%rbx
	ret

  • Each indented line in the code corresponds to a single machine instruction.

  • All information about local variable names or data types has been stripped away.

If we use the -c command-line option, gcc will both compile and assemble the code

1
$ gcc -Og -c mstore.c

This will give us a binary file mstore.o

Embedded within the 1,368 bytes of the file mstore.o is a 14-byte sequence with the hexadecimal representation

1
2
$ hexdump -C mstore.o | grep '53 48 89 d3 e8 00 00 00  00 48 89 03 5b c3'
00000040  53 48 89 d3 e8 00 00 00  00 48 89 03 5b c3 00 47  |SH.......H..[..G|

This is the object code corresponding to the assembly instructions listed previously

A key lesson to learn from this is that the program executed by the machine is simply a sequence of bytes encoding a series of instructions. The machine has very little information about the source code from which these instructions were generated.

Programs call disassembler generate a format similar to assembly code from the machine code.

1
$ objdump -d mstore.o
1
2
3
4
5
6
7
8
9
10
11
mstore.o:     file format elf64-x86-64

Disassembly of section .text:

0000000000000000 <multstore>:
   0:	53                   	push   %rbx
   1:	48 89 d3             	mov    %rdx,%rbx
   4:	e8 00 00 00 00       	callq  9 <multstore+0x9>
   9:	48 89 03             	mov    %rax,(%rbx)
   c:	5b                   	pop    %rbx
   d:	c3                   	retq

Several features about machine code and its disassembled representation are worth noting:

  • x86-64 instructions can range in length from 1 to 15 bytes. The instruction encoding is designed so that commonly used instructions and those with fewer operands require a smaller number of bytes than do less common ones or ones with more operands.

  • The instruction format is designed in such a way that from a given starting position, there is a unique decoding of the bytes into machine instructions. For example, only the instruction pushq %rbx can start with byte value 53.

  • The disassembler determines the assembly code based purely on the byte sequences in the machine-code file. It does not require access to the source or assembly-code versions of the program.

  • The disassembler uses a slightly different naming convention for the instructions than does the assembly code generated by gcc.

    In our example, it has omitted the suffix q from many of the instructions. These suffixes are size designators and can be omitted in most cases. Conversely, the disassembler adds the suffix q to the call and ret instructions. Again, these suffixes can safely be omitted.

Generating the actual executable code requires running a linker on the set of object-code files, one of which must contain a function main.

1
2
3
4
5
6
7
8
9
10
11
12
13
//source of main.c
#include <stdio.h>
void multstore(long, long, long *);
int main() {
long d;
multstore(2, 3, &d);
printf("2 * 3 --> %ld\n", d);
return 0;
}
long mult2(long a, long b) {
long s = a * b;
return s;
}
1
$ gcc -Og -o prog main.c mstore.c

The file prog has grown to 8,655 bytes, since it contains not just the machine code for the procedures we provided but also code used to start and terminate the program as well as to interact with the operating system.

We can disassemble the file prog:

1
$ objdump -d prog
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
prog:     file format elf64-x86-64
Disassembly of section .init:

0000000000000570 <_init>:
 570:	48 83 ec 08          	sub    $0x8,%rsp
 574:	48 8b 05 6d 0a 20 00 	mov    0x200a6d(%rip),%rax        # 200fe8 <__gmon_start__>
 57b:	48 85 c0             	test   %rax,%rax
 57e:	74 02                	je     582 <_init+0x12>
 580:	ff d0                	callq  *%rax
 582:	48 83 c4 08          	add    $0x8,%rsp
 586:	c3                   	retq   
Disassembly of section .plt:

0000000000000590 <.plt>:
 590:	ff 35 22 0a 20 00    	pushq  0x200a22(%rip)        # 200fb8 <_GLOBAL_OFFSET_TABLE_+0x8>
 596:	ff 25 24 0a 20 00    	jmpq   *0x200a24(%rip)        # 200fc0 <_GLOBAL_OFFSET_TABLE_+0x10>
 59c:	0f 1f 40 00          	nopl   0x0(%rax)

00000000000005a0 <__stack_chk_fail@plt>:
 5a0:	ff 25 22 0a 20 00    	jmpq   *0x200a22(%rip)        # 200fc8 <__stack_chk_fail@GLIBC_2.4>
 5a6:	68 00 00 00 00       	pushq  $0x0
 5ab:	e9 e0 ff ff ff       	jmpq   590 <.plt>

00000000000005b0 <__printf_chk@plt>:
 5b0:	ff 25 1a 0a 20 00    	jmpq   *0x200a1a(%rip)        # 200fd0 <__printf_chk@GLIBC_2.3.4>
 5b6:	68 01 00 00 00       	pushq  $0x1
 5bb:	e9 d0 ff ff ff       	jmpq   590 <.plt>

Disassembly of section .plt.got:

00000000000005c0 <__cxa_finalize@plt>:
 5c0:	ff 25 32 0a 20 00    	jmpq   *0x200a32(%rip)        # 200ff8 <__cxa_finalize@GLIBC_2.2.5>
 5c6:	66 90                	xchg   %ax,%ax

Disassembly of section .text:

00000000000005d0 <_start>:
 5d0:	31 ed                	xor    %ebp,%ebp
 5d2:	49 89 d1             	mov    %rdx,%r9
 5d5:	5e                   	pop    %rsi
 5d6:	48 89 e2             	mov    %rsp,%rdx
 5d9:	48 83 e4 f0          	and    $0xfffffffffffffff0,%rsp
 5dd:	50                   	push   %rax
 5de:	54                   	push   %rsp
 5df:	4c 8d 05 da 01 00 00 	lea    0x1da(%rip),%r8        # 7c0 <__libc_csu_fini>
 5e6:	48 8d 0d 63 01 00 00 	lea    0x163(%rip),%rcx        # 750 <__libc_csu_init>
 5ed:	48 8d 3d e6 00 00 00 	lea    0xe6(%rip),%rdi        # 6da <main>
 5f4:	ff 15 e6 09 20 00    	callq  *0x2009e6(%rip)        # 200fe0 <__libc_start_main@GLIBC_2.2.5>
 5fa:	f4                   	hlt    
 5fb:	0f 1f 44 00 00       	nopl   0x0(%rax,%rax,1)

0000000000000600 <deregister_tm_clones>:
 600:	48 8d 3d 09 0a 20 00 	lea    0x200a09(%rip),%rdi        # 201010 <__TMC_END__>
 607:	55                   	push   %rbp
 608:	48 8d 05 01 0a 20 00 	lea    0x200a01(%rip),%rax        # 201010 <__TMC_END__>
 60f:	48 39 f8             	cmp    %rdi,%rax
 612:	48 89 e5             	mov    %rsp,%rbp
 615:	74 19                	je     630 <deregister_tm_clones+0x30>
 617:	48 8b 05 ba 09 20 00 	mov    0x2009ba(%rip),%rax        # 200fd8 <_ITM_deregisterTMCloneTable>
 61e:	48 85 c0             	test   %rax,%rax
 621:	74 0d                	je     630 <deregister_tm_clones+0x30>
 623:	5d                   	pop    %rbp
 624:	ff e0                	jmpq   *%rax
 626:	66 2e 0f 1f 84 00 00 	nopw   %cs:0x0(%rax,%rax,1)
 62d:	00 00 00 
 630:	5d                   	pop    %rbp
 631:	c3                   	retq   
 632:	0f 1f 40 00          	nopl   0x0(%rax)
 636:	66 2e 0f 1f 84 00 00 	nopw   %cs:0x0(%rax,%rax,1)
 63d:	00 00 00 

0000000000000640 <register_tm_clones>:
 640:	48 8d 3d c9 09 20 00 	lea    0x2009c9(%rip),%rdi        # 201010 <__TMC_END__>
 647:	48 8d 35 c2 09 20 00 	lea    0x2009c2(%rip),%rsi        # 201010 <__TMC_END__>
 64e:	55                   	push   %rbp
 64f:	48 29 fe             	sub    %rdi,%rsi
 652:	48 89 e5             	mov    %rsp,%rbp
 655:	48 c1 fe 03          	sar    $0x3,%rsi
 659:	48 89 f0             	mov    %rsi,%rax
 65c:	48 c1 e8 3f          	shr    $0x3f,%rax
 660:	48 01 c6             	add    %rax,%rsi
 663:	48 d1 fe             	sar    %rsi
 666:	74 18                	je     680 <register_tm_clones+0x40>
 668:	48 8b 05 81 09 20 00 	mov    0x200981(%rip),%rax        # 200ff0 <_ITM_registerTMCloneTable>
 66f:	48 85 c0             	test   %rax,%rax
 672:	74 0c                	je     680 <register_tm_clones+0x40>
 674:	5d                   	pop    %rbp
 675:	ff e0                	jmpq   *%rax
 677:	66 0f 1f 84 00 00 00 	nopw   0x0(%rax,%rax,1)
 67e:	00 00 
 680:	5d                   	pop    %rbp
 681:	c3                   	retq   
 682:	0f 1f 40 00          	nopl   0x0(%rax)
 686:	66 2e 0f 1f 84 00 00 	nopw   %cs:0x0(%rax,%rax,1)
 68d:	00 00 00 

0000000000000690 <__do_global_dtors_aux>:
 690:	80 3d 79 09 20 00 00 	cmpb   $0x0,0x200979(%rip)        # 201010 <__TMC_END__>
 697:	75 2f                	jne    6c8 <__do_global_dtors_aux+0x38>
 699:	48 83 3d 57 09 20 00 	cmpq   $0x0,0x200957(%rip)        # 200ff8 <__cxa_finalize@GLIBC_2.2.5>
 6a0:	00 
 6a1:	55                   	push   %rbp
 6a2:	48 89 e5             	mov    %rsp,%rbp
 6a5:	74 0c                	je     6b3 <__do_global_dtors_aux+0x23>
 6a7:	48 8b 3d 5a 09 20 00 	mov    0x20095a(%rip),%rdi        # 201008 <__dso_handle>
 6ae:	e8 0d ff ff ff       	callq  5c0 <__cxa_finalize@plt>
 6b3:	e8 48 ff ff ff       	callq  600 <deregister_tm_clones>
 6b8:	c6 05 51 09 20 00 01 	movb   $0x1,0x200951(%rip)        # 201010 <__TMC_END__>
 6bf:	5d                   	pop    %rbp
 6c0:	c3                   	retq   
 6c1:	0f 1f 80 00 00 00 00 	nopl   0x0(%rax)
 6c8:	f3 c3                	repz retq 
 6ca:	66 0f 1f 44 00 00    	nopw   0x0(%rax,%rax,1)

00000000000006d0 <frame_dummy>:
 6d0:	55                   	push   %rbp
 6d1:	48 89 e5             	mov    %rsp,%rbp
 6d4:	5d                   	pop    %rbp
 6d5:	e9 66 ff ff ff       	jmpq   640 <register_tm_clones>

00000000000006da <main>:
 6da:	48 83 ec 18          	sub    $0x18,%rsp
 6de:	64 48 8b 04 25 28 00 	mov    %fs:0x28,%rax
 6e5:	00 00 
 6e7:	48 89 44 24 08       	mov    %rax,0x8(%rsp)
 6ec:	31 c0                	xor    %eax,%eax
 6ee:	48 89 e2             	mov    %rsp,%rdx
 6f1:	be 03 00 00 00       	mov    $0x3,%esi
 6f6:	bf 02 00 00 00       	mov    $0x2,%edi
 6fb:	e8 41 00 00 00       	callq  741 <multstore>
 700:	48 8b 14 24          	mov    (%rsp),%rdx
 704:	48 8d 35 c9 00 00 00 	lea    0xc9(%rip),%rsi        # 7d4 <_IO_stdin_used+0x4>
 70b:	bf 01 00 00 00       	mov    $0x1,%edi
 710:	b8 00 00 00 00       	mov    $0x0,%eax
 715:	e8 96 fe ff ff       	callq  5b0 <__printf_chk@plt>
 71a:	48 8b 4c 24 08       	mov    0x8(%rsp),%rcx
 71f:	64 48 33 0c 25 28 00 	xor    %fs:0x28,%rcx
 726:	00 00 
 728:	75 0a                	jne    734 <main+0x5a>
 72a:	b8 00 00 00 00       	mov    $0x0,%eax
 72f:	48 83 c4 18          	add    $0x18,%rsp
 733:	c3                   	retq   
 734:	e8 67 fe ff ff       	callq  5a0 <__stack_chk_fail@plt>

0000000000000739 <mult2>:
 739:	48 89 f8             	mov    %rdi,%rax
 73c:	48 0f af c6          	imul   %rsi,%rax
 740:	c3                   	retq   

0000000000000741 <multstore>:
 741:	53                   	push   %rbx
 742:	48 89 d3             	mov    %rdx,%rbx
 745:	e8 ef ff ff ff       	callq  739 <mult2>
 74a:	48 89 03             	mov    %rax,(%rbx)
 74d:	5b                   	pop    %rbx
 74e:	c3                   	retq   
 74f:	90                   	nop

0000000000000750 <__libc_csu_init>:
 750:	41 57                	push   %r15
 752:	41 56                	push   %r14
 754:	49 89 d7             	mov    %rdx,%r15
 757:	41 55                	push   %r13
 759:	41 54                	push   %r12
 75b:	4c 8d 25 4e 06 20 00 	lea    0x20064e(%rip),%r12        # 200db0 <__frame_dummy_init_array_entry>
 762:	55                   	push   %rbp
 763:	48 8d 2d 4e 06 20 00 	lea    0x20064e(%rip),%rbp        # 200db8 <__init_array_end>
 76a:	53                   	push   %rbx
 76b:	41 89 fd             	mov    %edi,%r13d
 76e:	49 89 f6             	mov    %rsi,%r14
 771:	4c 29 e5             	sub    %r12,%rbp
 774:	48 83 ec 08          	sub    $0x8,%rsp
 778:	48 c1 fd 03          	sar    $0x3,%rbp
 77c:	e8 ef fd ff ff       	callq  570 <_init>
 781:	48 85 ed             	test   %rbp,%rbp
 784:	74 20                	je     7a6 <__libc_csu_init+0x56>
 786:	31 db                	xor    %ebx,%ebx
 788:	0f 1f 84 00 00 00 00 	nopl   0x0(%rax,%rax,1)
 78f:	00 
 790:	4c 89 fa             	mov    %r15,%rdx
 793:	4c 89 f6             	mov    %r14,%rsi
 796:	44 89 ef             	mov    %r13d,%edi
 799:	41 ff 14 dc          	callq  *(%r12,%rbx,8)
 79d:	48 83 c3 01          	add    $0x1,%rbx
 7a1:	48 39 dd             	cmp    %rbx,%rbp
 7a4:	75 ea                	jne    790 <__libc_csu_init+0x40>
 7a6:	48 83 c4 08          	add    $0x8,%rsp
 7aa:	5b                   	pop    %rbx
 7ab:	5d                   	pop    %rbp
 7ac:	41 5c                	pop    %r12
 7ae:	41 5d                	pop    %r13
 7b0:	41 5e                	pop    %r14
 7b2:	41 5f                	pop    %r15
 7b4:	c3                   	retq   
 7b5:	90                   	nop
 7b6:	66 2e 0f 1f 84 00 00 	nopw   %cs:0x0(%rax,%rax,1)
 7bd:	00 00 00 

00000000000007c0 <__libc_csu_fini>:
 7c0:	f3 c3                	repz retq 

Disassembly of section .fini:

00000000000007c4 <_fini>:
 7c4:	48 83 ec 08          	sub    $0x8,%rsp
 7c8:	48 83 c4 08          	add    $0x8,%rsp
 7cc:	c3                   	retq

Note that this the codes of multstore hold.

1
2
3
4
5
6
7
8
0000000000000741 <multstore>:
 741:	53                   	push   %rbx
 742:	48 89 d3             	mov    %rdx,%rbx
 745:	e8 ef ff ff ff       	callq  739 <mult2>
 74a:	48 89 03             	mov    %rax,(%rbx)
 74d:	5b                   	pop    %rbx
 74e:	c3                   	retq   
 74f:	90                   	nop

  • One important difference is that the addresses listed along the left are different— the linker has shifted the location of this code to a different range of addresses.

  • A second difference is that the linker has filled in the address that the callq instruction should use in calling the function mult2. One task for the linker is to match function calls with the locations of the executable code for those functions.

  • A final difference is that we see one additional lines of code nop. This instruction will have no effect on the program, since it occurs after the return instruction.

    It has been inserted to grow the code, enabling a better placement of the next block of code in terms of memory system performance.

3.2.3 Notes on Formatting

The assembly code generated by gcc contains information with which we need not be concerned and does not provide any description of the program or how it works.

1
$ cat mstore.s
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
	.file	"mstore.c"
	.text
	.globl	multstore
	.type	multstore, @function
multstore:
.LFB0:
	.cfi_startproc
	pushq	%rbx
	.cfi_def_cfa_offset 16
	.cfi_offset 3, -16
	movq	%rdx, %rbx
	call	mult2@PLT
	movq	%rax, (%rbx)
	popq	%rbx
	.cfi_def_cfa_offset 8
	ret
	.cfi_endproc
.LFE0:
	.size	multstore, .-multstore
	.ident	"GCC: (Ubuntu 7.5.0-3ubuntu1~18.04) 7.5.0"
	.section	.note.GNU-stack,"",@progbits

All of the lines beginning with ‘.’ are directives to guide the assembler and linker. We can generally ignore these.

We will do two main task:

  1. omits most of the directives which begin with ‘.’

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    #!/usr/bin/python3
    # source of wash.py
    import sys
    clothes = sys.argv[1]
    f = open(clothes , 'rt')
    after = open('clean_' + clothes , 'wt' )
    ls = []
    for line in f:
        if line.strip()[0] != '.'  or len(line.strip()) == 4 :
            ls.append(line)
    after.writelines(ls)
    f.close()
    after.close()

  2. add some annotation(Unfortunately, this can only be done manually)

1
2
3
4
5
6
7
8
9
#void multstore(long x, long y, long *dest)
#x in %rdi, y in %rsi, dest in %rdx
multstore:
 pushq %rbx 		;Save %rbx
 movq %rdx, %rbx 	;Copy dest to %rbx
 call mult2 		;Call mult2(x, y)
 movq %rax, (%rbx) 	;Store result at *dest
 popq %rbx 			;Restore %rbx
 ret 				;Return
1
2
3
4
5
6
7
8
; intel format
multstore:
	push	rbx
	mov	rbx, rdx
	call	mult2@PLT
	mov	QWORD PTR [rbx], rax
	pop	rbx
	ret

Difference between ATT format and intel format

ATT(name after AT&T) fomat is the default format for gcc, objdump, and the other tools we will consider.

intel format is from Microsoft, it can be shown by telling gcc -masm=intel

  • The Intel code omits the size designation suffixes. We see instruction push and mov instead of pushq and movq.
  • The Intel code omits the % character in front of register names, using rbx instead of %rbx
  • The Intel code has a different way of describing locations in memory—for example, QWORD PTR [rbx] rather than (%rbx).
  • Instructions with multiple operands list them in the reverse order. This can be very confusing when switching between the two formats!!!

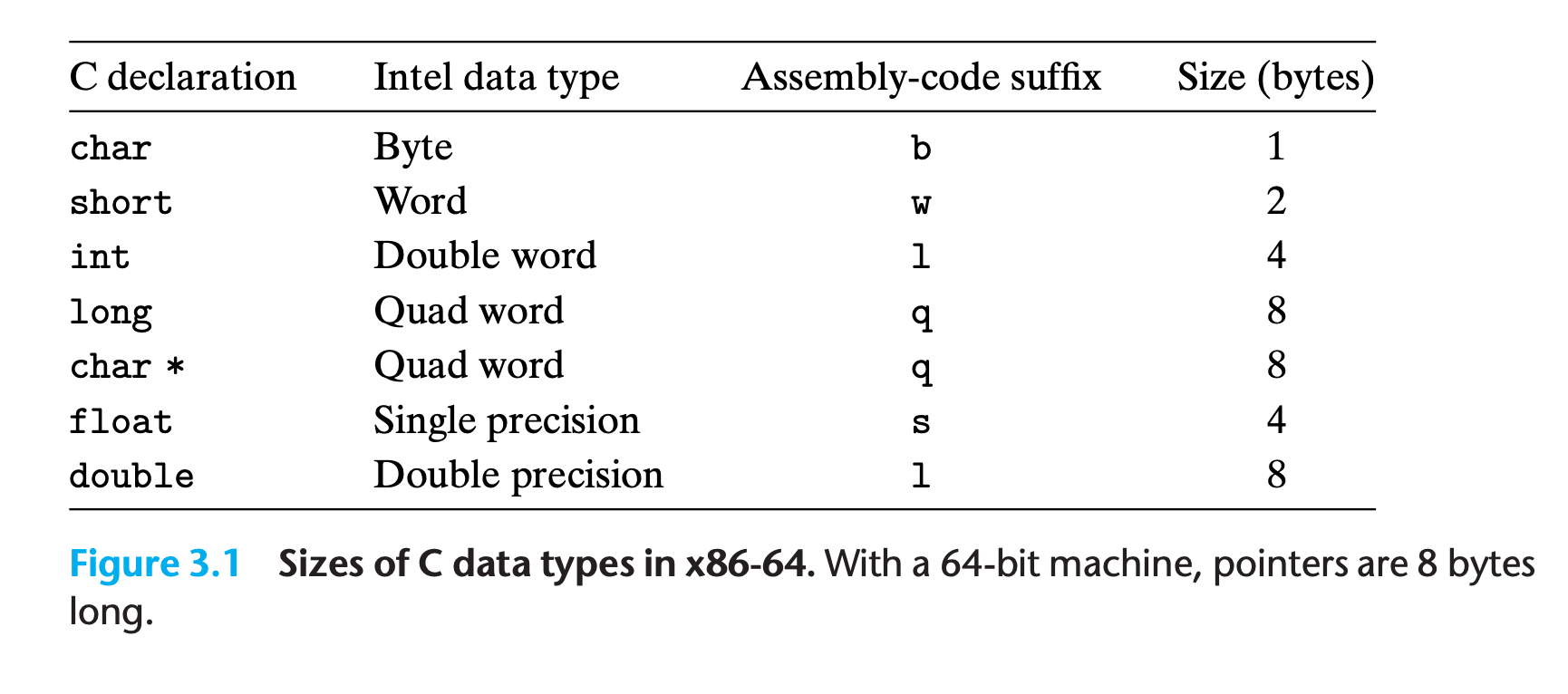
3.3 Data Formats

Intel uses the term “word” to refer to a 16-bit data type. Based on this, they refer to 32- bit quantities as “double words,” and 64-bit quantities as “quad words.”

sizeof

Microprocessors in the x86 family historically implemented all floating-point operations with a special 80-bit floating-point format. This format can be specified in C programs using the declaration long double.

We recommend against using this format, however.

  • It is not portable to other classes of machines
  • it is typically not implemented with the same high-performance hardware as is the case for single- and double-precision arithmetic.

most assembly-code instructions generated by gcc have a single-character suffix denoting the size of the operand.

For example, the data movement instruction has four variants:

  • movb (move byte), movw (move word), movl (move double word), and movq (move quad word).
  • The suffix ‘l’ is used for double words, since 32-bit quantities are considered to be “long words.”

The assembly code uses the suffix l to denote a 4-byte integer as well as an 8-byte double-precision floating-point number. This causes no ambiguity, since floating-point code involves an entirely different set of instructions and registers.

3.4 Accessing Information

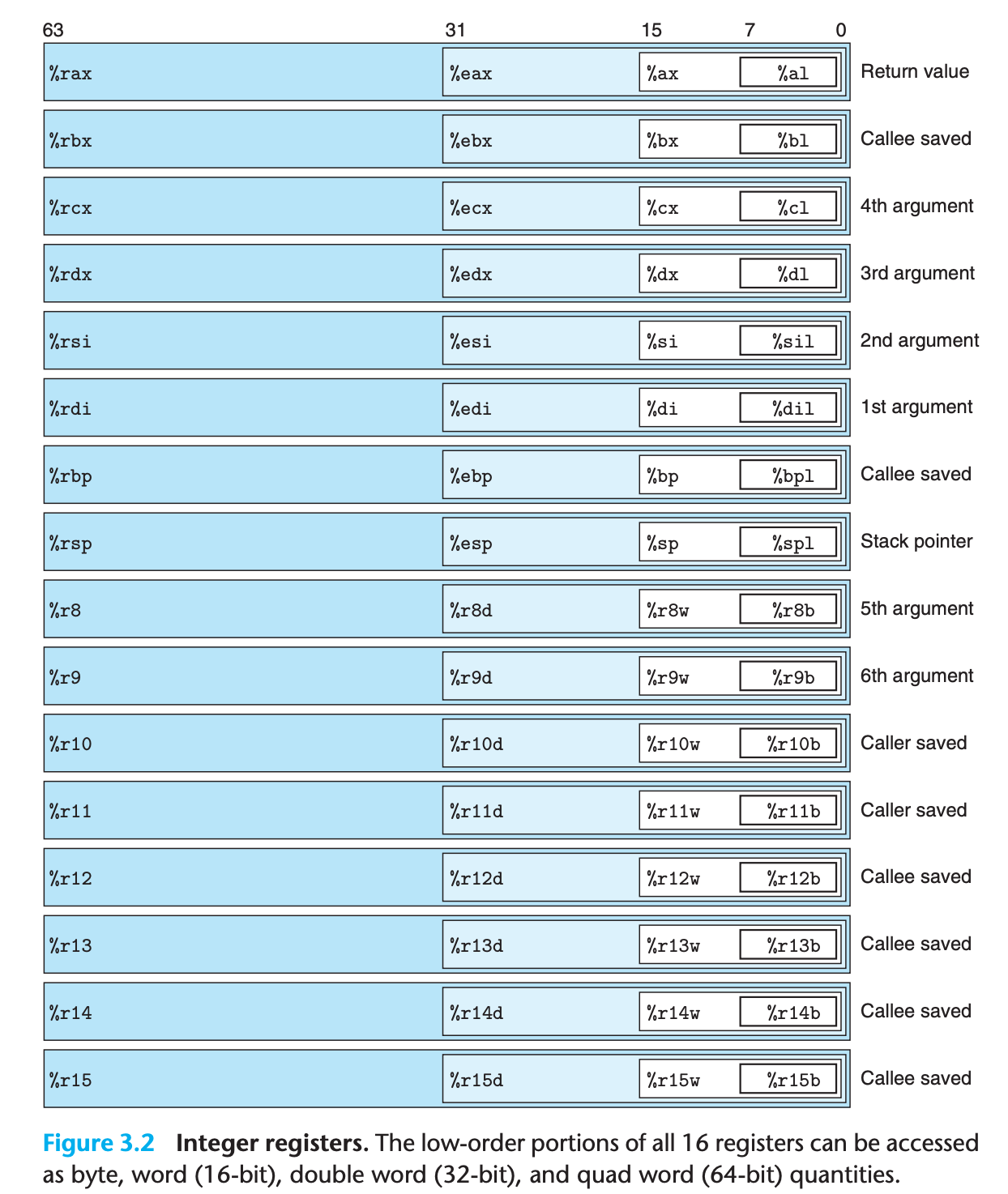
An x86-64 central processing unit (CPU) contains a set of 16 general-purpose registers storing 64-bit values.

  • Their names all begin with %r(short for register), but otherwise follow multiple different naming conventions, owing to the historical evolution of the instruction set.

    • The original 8086 had eight 16-bit registers. Each had a specific purpose, and hence they were given names that reflected how they were to be used.

    • With the extension to IA32, these registers were expanded to 32-bit registers, labeled %eax through %ebp(short for extended).

    • In the extension to x86-64, the original eight registers were expanded to 64 bits, labeled %rax through %rbp.

    • In addition, eight new registers were added, and these were given labels according to a new naming convention: %r8 through %r15

  • instructions can operate on data of different sizes stored in the low-order bytes of the 16 registers.

    • Byte-level operations can access the least significant byte, 16-bit operations can access the least significant 2 bytes, 32-bit operations can access the least significant 4 bytes, and 64-bit operations can access entire registers.

  • When instructions for copying and generating 1-, 2-, 4-, and 8-byte values have registers as destinations, two conventions arise for what happens to the remaining bytes in the register for instructions that generate less than 8 bytes:

    • Those that generate 1- or 2-byte quantities leave the remaining bytes unchanged.
    • Those that generate 4- byte quantities set the upper 4 bytes of the register to zero.
    • The latter convention was adopted as part of the expansion from IA32 to x86-64

registers

3.4.1 Operand Specifiers

Most instructions have one or more operands specifying the source values to use in performing an operation and the destination location into which to place the result

Source values can be given as constants or read from registers or memory.

Results can be stored in either registers or memory.

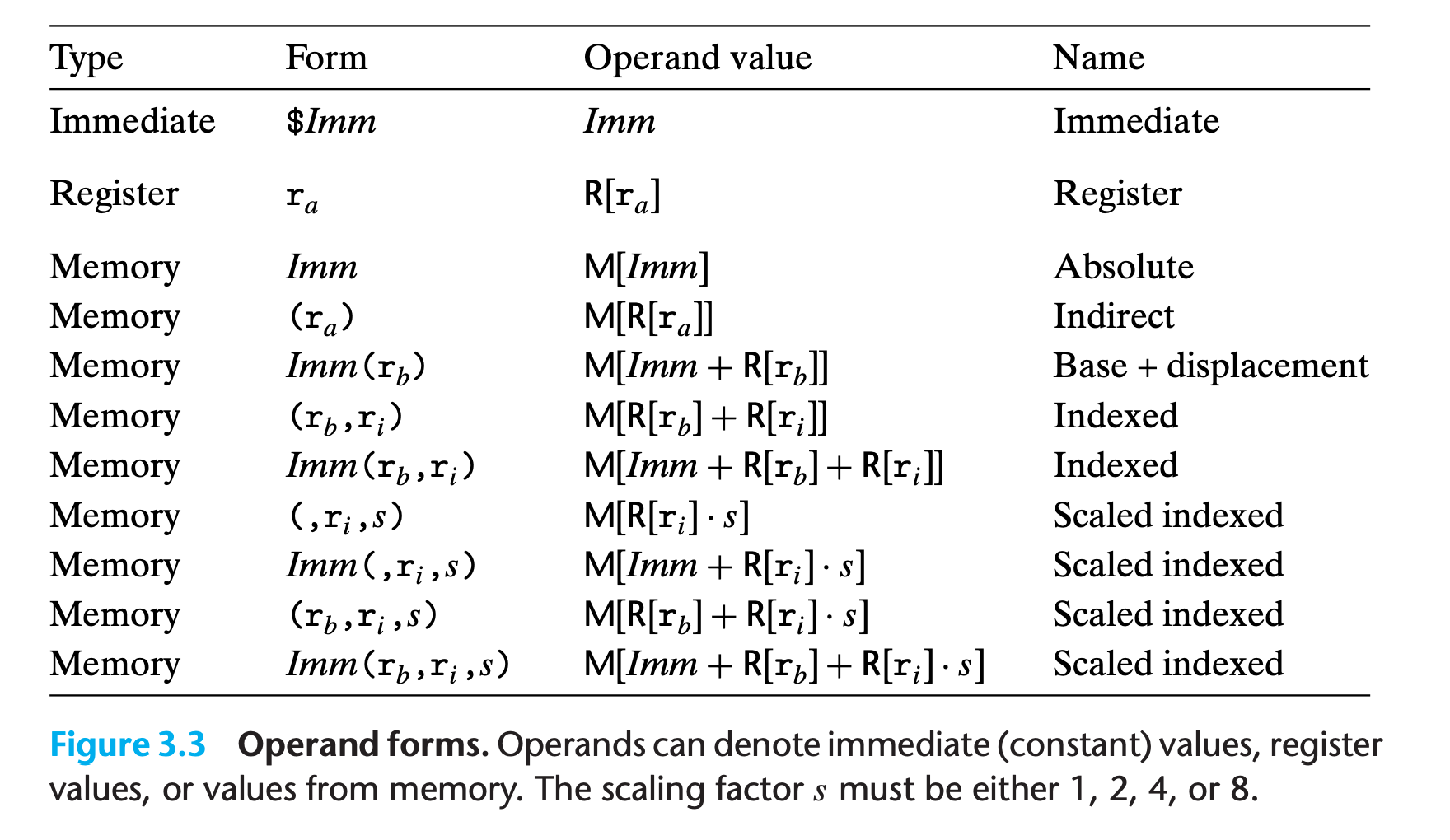
operand forms

  • The first type, immediate, is for constant values.

    • In ATTformat assembly code, these are written with a $ followed by an integer using standard C notation—for example, $-577 or $0x1F.
    • Different instructions allow different ranges of immediate values.
    • The assembler will automatically select the most compact way of encoding a value

  • The second type, register, denotes the contents of a register, one of the sixteen 8-, 4-, 2-, or 1-byte low-order portions of the registers for operands having 64, 32, 16, or 8 bits, respectively.

    • we use the notation $r_a$ to denote an arbitrary register a and indicate its value with the reference R[$r_a$​], viewing the set of registers as an array R indexed by register identifiers.

  • The third type of operand is a memory reference, in which we access some memory location according to a computed address, often called the effective address.

    • Since we view the memory as a large array of bytes, we use the notation $M_b[Addr]$ to denote a reference to the b-byte value stored in memory starting at address $Addr$. To simplify things, we will generally drop the subscript $b$.

    • There are many different addressing modes allowing different forms of memory references. The most general form is shown at the bottom of the table with syntax $Imm(r_b,r_i,s)$.

      • Such a reference has four components: an immediate offset $Imm$, a base register $r_b$, an index register $r_i$, and a scale factor s, where s must be 1, 2, 4, or 8. Both the base and index must be 64-bit registers.

      • The effective address is computed as $Imm + R[r_b] + R[r_i] \cdot s$.

      • This general form is often seen when referencing elements of arrays.

        The other forms are simply special cases of this general form where some of the components are omitted.

      • the more complex addressing modes are useful when referencing array and structure elements.

Practice Problem 3.1

Assume the following values are stored at the indicated memory addresses and registers:

Address Value Register Value
0x100 0xFF %rax 0x100
0x104 0xAB %rcx 0x1
0x108 0x13 %rdx 0x3
0x10C 0x11

Fill in the following table showing the values for the indicated operands:

Operand Value
%rax
0x104
$0x108
(%rax)
4(%rax)
9(%rax,%rdx)
260(%rcx , %rdx)
0xFC(,%rcx,4)
(%rax,%rdx,4)

My solution: :white_check_mark:

Operand Value
%rax 0x100
0x104 0xAB
$0x108 0x108
(%rax) 0xFF
4(%rax) 0xAB
9(%rax,%rdx) 0x11
260(%rcx , %rdx) 0x13
0xFC(,%rcx,4) 0xFF
(%rax,%rdx,4) 0x11

3.4.2 Data Movement Instructions

Among the most heavily used instructions are those that copy data from one location to another.

In our presentation, we group the many different instructions into instruction classes, where the instructions in a class perform the same operation but with different operand sizes.

mov class

These instructions copy data from a source location to a destination location, without any transformation.

mov

  • x86-64 imposes the restriction that a move instruction cannot have both operands refer to memory locations.

    • Copying a value from one memory location to another requires two instructions—the first to load the source value into a register, and the second to write this register value to the destination.

  • For most cases, the mov instructions will only update the specific register bytes or memory locations indicated by the destination operand.

    The only exception is that when movl has a register as the destination, it will also set the high-order 4 bytes of the register to 0.

Examples

1
2
3
4
5
movl $0x4050,%eax 		Immediate--Register, 	4 bytes
movw %bp,%sp 			Register--Register, 	2 bytes
movb (%rdi,%rcx),%al 	Memory--Register, 		1 byte
movb $-17,(%esp) 		Immediate--Memory, 		1 byte
movq %rax,-12(%rbp) 	Register--Memory, 		8 bytes

The regular movq instruction can only have immediate source operands that can be represented as 32-bit two’s-complement numbers. This value is then sign extended to produce the 64-bit value for the destination.

The movabsq instruction can have an arbitrary 64-bit immediate value as its source operand and can only have a register as a destination

movz and movs classes

when copying a smaller source value to a larger destination.

  • Instructions in the movz class fill out the remaining bytes of the destination with zeros, while those in the movs class fill them out by sign extension, replicating copies of the most significant bit of the source operand.

  • Each instruction name has size designators as its final two characters—the first specifying the source size, and the second specifying the destination size.

movz

movs

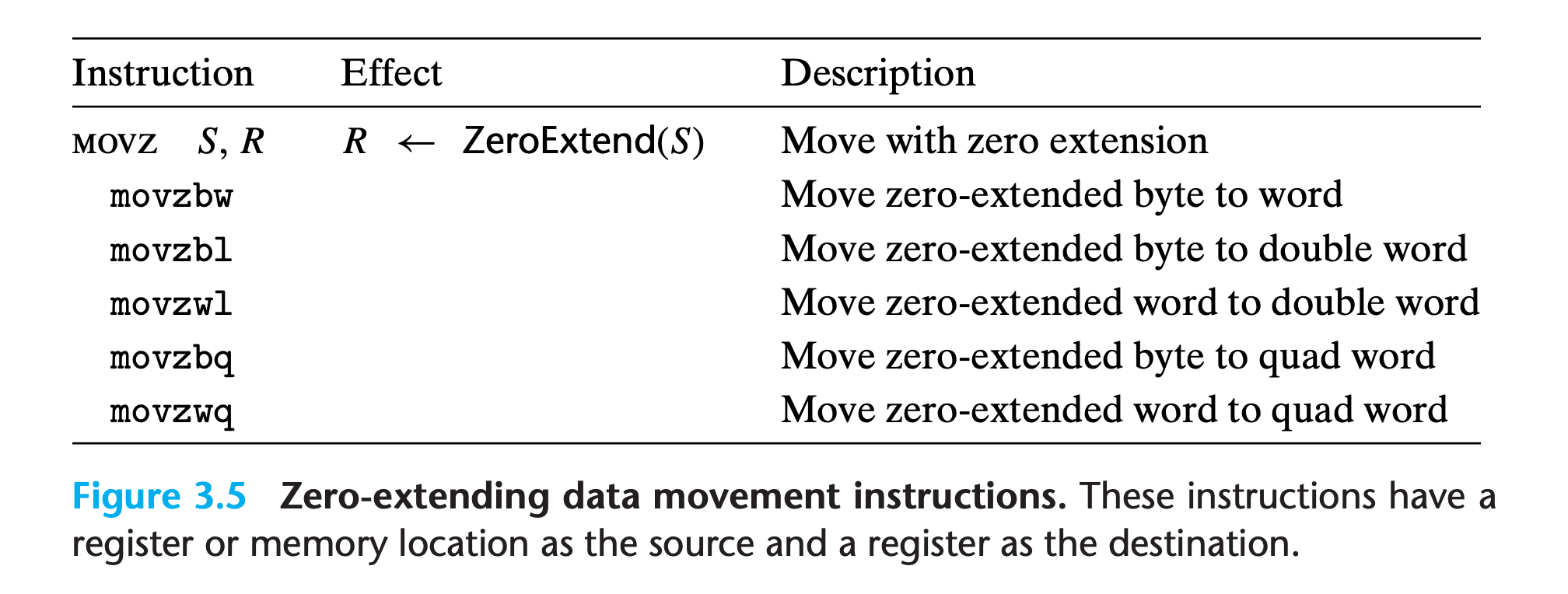
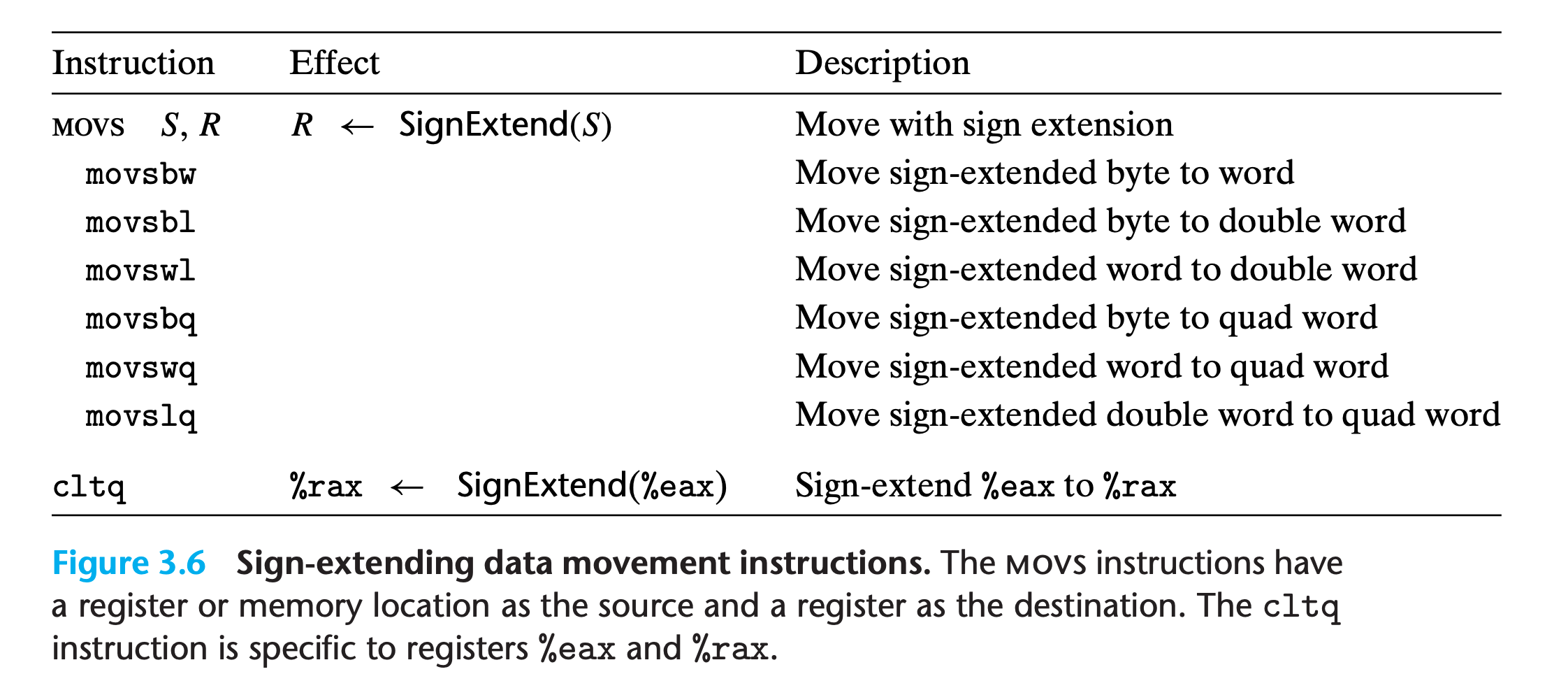
  • Note the absence of an explicit instruction to zero-extend a 4-byte source value to an 8-byte destination can be implemented using a movl instruction having a register as the destination, logically if there do exist one, it should be named movzlq

    This technique takes advantage of the property that an instruction generating a 4-byte value with a register as the destination will fill the upper 4 bytes with zeros.

  • cltq stands for “convert long to quad”, in intel style this will be cdqe (convert double to quad extend), it has the exact same effect as the instruction movslq %eax, %rax, but it has a more compact encoding.

Practice Problem 3.2

For each of the following lines of assembly language, determine the appropriate instruction suffix based on the operands. (For example, mov can be rewritten as movb, movw, movl, or movq.)

1
2
3
4
5
6
mov %eax, (%rsp)
mov (%rax), %dx
mov $0xFF, %bl
mov (%rsp,%rdx,4), %dl
mov (%rdx), %rax
mov %dx, (%rax)

My solution: :white_check_mark:

1
2
3
4
5
6
movl %eax, (%rsp)
movw (%rax) , %dx
movb $0xFF , %bl
movb (%rsp,%rdx,4), %dl
movq (%rdx), %rax
movw %dx, (%rax)

Practice Problem 3.3

Each of the following lines of code generates an error message when we invoke the assembler. Explain what is wrong with each line.

1
2
3
4
5
6
7
movb $0xF, (%ebx)
movl %rax, (%rsp)
movw (%rax),4(%rsp)
movb %al,%sl
movq %rax,$0x123
movl %eax,%rdx
movb %si, 8(%rbp)

My solution : :white_check_mark:

1
2
3
4
5
6
7
movb $0xF, (%ebx) ;in x86_64 address should always be 64 bits, %ebx is 32 bits
movl %rax, (%rsp) ;%rax is 64 bits , movl should be movq
movw (%rax),4(%rsp) ; direct copy between memory is forbidden
movb %al,%sl ; No register named %sl
movq %rax,$0x123 ; destination can't be an immediate value
movl %eax,%rdx ; %rdx should be %edx
movb %si, 8(%rbp); %si is 16 bits, movb should be movw

3.4.3 Data Movement Example

As an example of code that uses data movement instructions, consider the data exchange routine shown in below

1
2
3
4
5
6
long exchange(long *xp, long y)
{
long x = *xp;
*xp = y;
return x;
}
1
2
3
4
5
6
; long exchange(long *xp, long y)
; xp in %rdi, y in %rsi
; exchange:
 movq (%rdi), %rax 	;Get x at xp. Set as return value.
 movq %rsi, (%rdi) 	;Store y at xp.
 ret 				;Return.
  • First, we see that what we call “pointers” in C are simply addresses. Dereferencing a pointer involves copying that pointer into a register, and then using this register in a memory reference.
  • Second, local variables such as x are often kept in registers rather than stored in memory locations. Register access is much faster than memory access.

Practice Problem 3.4

Assume variables sp and dp are declared with types

1
2
src_t *sp;
dest_t *dp;

where src_t and dest_t are data types declared with typedef. We wish to use the appropriate pair of data movement instructions to implement the operation

1
*dp = (dest_t) *sp;

Assume that the values of sp and dp are stored in registers %rdi and %rsi, respectively.

For each entry in the table, show the two instructions that implement the specified data movement.

The first instruction in the sequence should read from memory, do the appropriate conversion, and set the appropriate portion of register %rax.

The second instruction should then write the appropriate portion of %rax to memory. In both cases, the portions may be %rax, %eax, %ax, or %al, and they may differ from one another.

Recall that when performing a cast that involves both a size change and a change of “signedness” in C, the operation should change the size first

1
2
3
4
5
6
7
8
9
10
11
12
13
14
src_t 			dest_t 			Instruction
long 			long 			movq (%rdi), %rax
								movq %rax, (%rsi)			
char 			int				

char 			unsigned

unsigned char 	long

int 			char

unsigned 		unsigned char

char 			short

My solution : :white_check_mark:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
src_t 			dest_t 			Instruction
long 			long 			movq (%rdi), %rax
								movq %rax, (%rsi)			
char 			int				movsbl (%rdi),%eax
								movl %eax,(%rsi)
char 			unsigned		movsbl (%rdi),%eax
								movl %eax , (%rsi)
unsigned char 	long			movzbl (%rdi),%eax
								movq %rax, (%rsi)
int 			char			movl (%rdi) , %eax
								movb %al , (%rsi)
unsigned 		unsigned char	movl (%rdi) , %eax
								movb %al , (%rsi)
char 			short			movsbw (%rdi) , %ax
								movw %ax,(%rsi)

Practice Problem 3.5

You are given the following information. A function with prototype

1
void decode1(long *xp, long *yp, long *zp);

is compiled into assembly code, yielding the following:

1
2
3
4
5
6
7
8
9
10
;void decode1(long *xp, long *yp, long *zp)
;xp in %rdi, yp in %rsi, zp in %rdx
decode1:
movq (%rdi), %r8
movq (%rsi), %rcx
movq (%rdx), %rax
movq %r8, (%rsi)
movq %rcx, (%rdx)
movq %rax, (%rdi)
ret

Parameters xp, yp, and zp are stored in registers %rdi, %rsi, and %rdx, respectively.

Write C code for decode1 that will have an effect equivalent to the assembly code shown.

My solution :

1
2
3
4
5
6
7
8
9
10
; %rdi = xp
; %rsi = yp
; %rdx = zp
movq (%rdi) , %r8. ; long temp = *xp    %r8 = *xp
movq (%rsi) , %rcx ; long temp2 = *yp   %rcx = *yp
movq (%rdx) , %rax ; long temp3 = *zp   %rax = *zp
movq %r8, (%rsi)   ; *yp = temp
movq %rcx , (%rdx) ; *zp = temp2
movq %rax, (%rdi)  ; *xp = temp3
ret
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void decode1(long *xp, long *yp, long *zp){
    long temp  = *xp ;
    long temp2 = *yp ;
    long temp3 = *zp ;
    *yp = temp ;
    *zp = temp2;
    *xp = temp3;
}

//or 
void decode2(long *xp, long *yp, long *zp){
    long temp = *xp ;
    *xp = *zp;
    *zp = *yp;
    *yp = temp;
}

Verification: :white_check_mark:

1
$ gcc -Og -S decode.c && ./wash.py decode.s && cat clean_decode.s
1
2
3
4
5
6
7
8
decode1:
	movq	(%rdi), %r8
	movq	(%rsi), %rcx
	movq	(%rdx), %rax
	movq	%r8, (%rsi)
	movq	%rcx, (%rdx)
	movq	%rax, (%rdi)
	ret
1
$ gcc -Og -S decode2.c && ./wash.py decode2.s && cat clean_decode2.s
1
2
3
4
5
6
7
8
decode2:
	movq	(%rdi), %rax
	movq	(%rdx), %rcx
	movq	%rcx, (%rdi)
	movq	(%rsi), %rcx
	movq	%rcx, (%rdx)
	movq	%rax, (%rsi)
	ret

Although use two less variables, we still get 7 instruction, no optimization !!!

3.4.4 Pushing and Popping Stack Data

The final two data movement operations are used to push data onto and pop data from the program stack, as documented in Figure.

The stack plays a vital role in the handling of procedure calls.

push pop

With x86-64, the program stack is stored in some region of memory.

The stack grows downward such that the top element of the stack has the lowest address of all stack elements

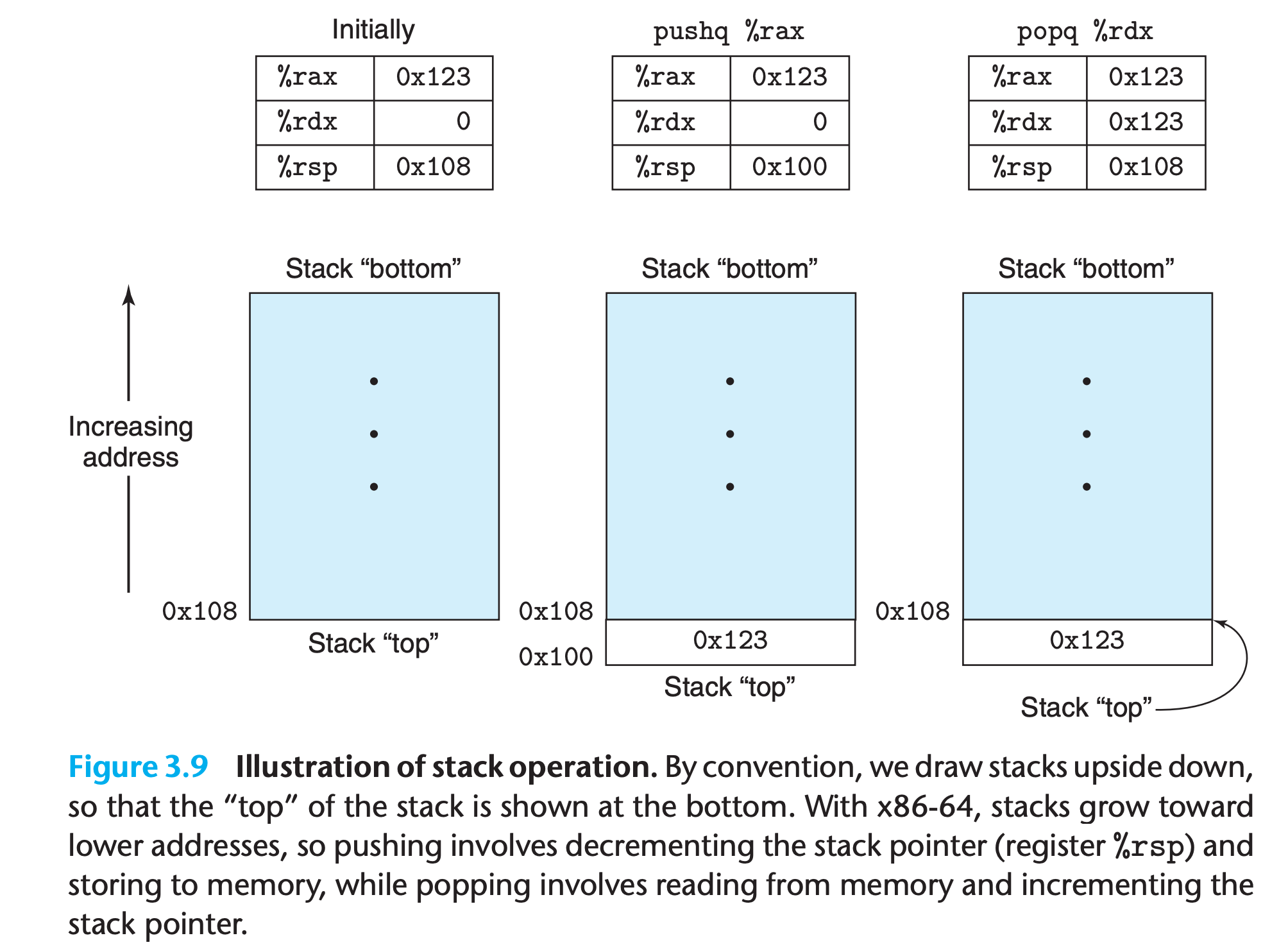
stack

  • The stack pointer %rsp holds the address of the top stack element
  • The pushq instruction provides the ability to push data onto the stack, while the popq instruction pops it. Each of these instructions takes a single operand—the data source for pushing and the data destination for popping.
Push

Pushing a quad word value onto the stack involves

  1. decrementing the stack pointer by 8
  2. writing the value at the new top-of-stack address.

Therefore, the behavior of the instruction pushq %rbp is equivalent to 

1
2
subq $8 , %rsp  	;Decrement stack pointer
movq %rbp , (%rsp) 	;Store %rbp on stack

The pushq instruction is encoded in the machine code as a single byte, whereas the pair of instructions shown above requires a total of 8 bytes.

Pop

Popping a quad word involves

  1. reading from the top-of-stack location
  2. incrementing the stack pointer by 8.

Therefore, the instruction popq %rax is equivalent to the following pair of instructions:

1
2
movq (%rsp),%rax 	;Read %rax from stack
addq $8,%rsp 		;Increment stack pointer

As shown in the figure, the ‘old’ stack top value remains in memory until it is overwritten

Stack

Since the stack is contained in the same memory as the program code and other forms of program data, programs can access arbitrary positions within the stack using the standard memory addressing methods.

3.5 Arithmetic and Logical Operations

Most of the operations are given as instruction classes, as they can have different variants with different operand sizes. Only leaq has no other size variants.(Address will always be 64 bits)

The operations are divided into four groups: load effective address, unary, binary, and shifts.

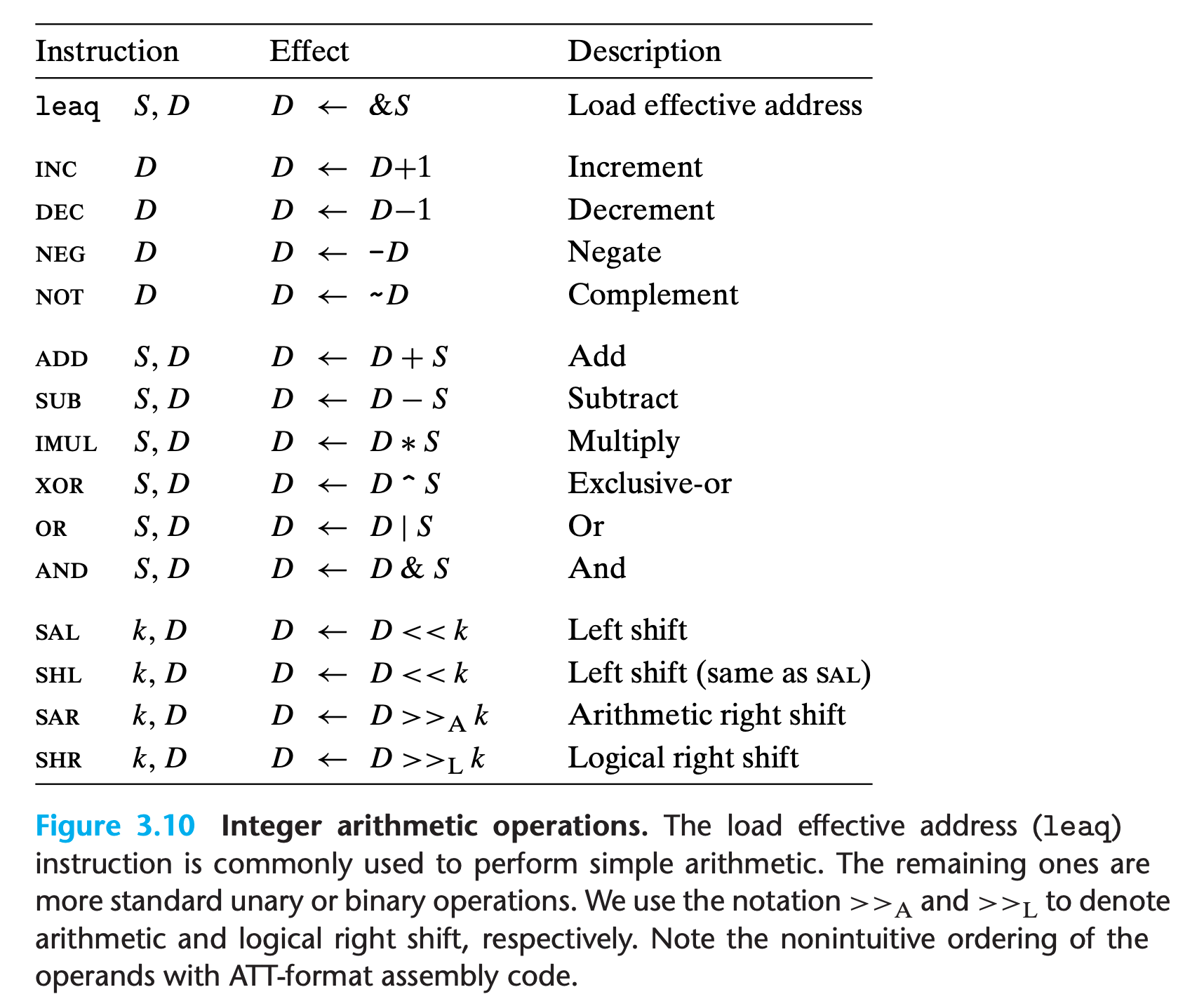
arithmetic operations

3.5.1 Load Effective Address

The load effective address instruction leaq is actually a variant of the movq instruction.

It has the form of an instruction that reads from memory to a register, but it does not reference memory at all !!!

  • Its first operand appears to be a memory reference, but instead of reading from the designated location, the instruction copies the effective address to the destination.

  • The instruction can be interpreted as C expression

    1
    2
    //leaq S,D
    Type * D = &S;

    This instruction can be used to generate pointers for later memory references

  • In addition, it can be used to compactly describe common arithmetic operations, as it shown in Chapter 2 D = x << y + z

    • For example, if register %rdx contains value x, then the instruction leaq 7(%rdx,%rdx,4), %rax will set register %rax to 5x + 7.
    • %rax = 7 + %rdx + %rdx * 4 = 5* %rdx + 7
    • Compilers often find clever uses of leaq that have nothing to do with effective address computations.

  • The destination operand must be a register.

Practice Problem 3.6

Suppose register %rbx holds value p and %rdx holds value q. Fill in the table below with formulas indicating the value that will be stored in register %rax for each of the given assembly-code instructions:

1
2
3
4
5
6
7
Instruction 					Result
leaq 	9(%rdx), %rax
leaq 	(%rdx,%rbx), %rax
leaq 	(%rdx,%rbx,3), %rax
leaq 	2(%rbx,%rbx,7), %rax
leaq 	0xE(,%rdx,3), %rax
leaq 	6(%rbx,%rdx,7), %rax

My solution : :white_check_mark:

1
2
3
4
5
6
7
8
9
#%rbx = p
#%rdx = q
Instruction 					Result
leaq 	9(%rdx), %rax			9 + q
leaq 	(%rdx,%rbx), %rax		q + p
leaq 	(%rdx,%rbx,3), %rax		q + 3p
leaq 	2(%rbx,%rbx,7), %rax	2 + 8p
leaq 	0xE(,%rdx,3), %rax		14 + 3q
leaq 	6(%rbx,%rdx,7), %rax	6 + p + 7q

As an illustration of the use of leaq in compiled code, consider the following C program:

1
2
3
4
long scale(long x, long y, long z) {
long t = x + 4 * y + 12 * z;
return t;
}

When compiled, the arithmetic operations of the function are implemented by a sequence of three leaq functions

1
2
3
4
5
6
7
# long scale(long x, long y, long z)
# x in %rdi, y in %rsi, z in %rdx
scale:
leaq (%rdi,%rsi,4), %rax 	#x + 4*y
leaq (%rdx,%rdx,2), %rdx 	#z + 2*z = 3*z
leaq (%rax,%rdx,4), %rax 	#(x+4*y) + 4*(3*z) = x + 4*y + 12*z
ret

(When compiling the codes, -O1 argument should be used)

Practice Problem 3.7

Consider the following code, in which we have omitted the expression being computed:

1
2
3
4
short scale3(short x, short y, short z) {
short t =   ___________ ;
return t;
}

Compiling the actual function with gcc yields the following assembly code:

1
2
3
4
5
6
7
# short scale3(short x, short y, short z)
# x in %rdi, y in %rsi, z in %rdx
scale3:
leaq (%rsi,%rsi,9), %rbx
leaq (%rbx,%rdx), %rbx
leaq (%rbx,%rdi,%rsi), %rbx
ret

Fill in the missing expression in the C code.

My solution : :white_check_mark:

1
2
3
4
5
6
7
# short scale3(short x, short y, short z)
# x in %rdi, y in %rsi, z in %rdx
scale3:
leaq (%rsi,%rsi,9), %rbx  # %rbx = 10 * y
leaq (%rbx,%rdx), %rbx	  # %rbx = 10*y + z
leaq (%rbx,%rdi,%rsi), %rbx # %rbx = 10 *y + z + x*y
ret
1
2
3
4
short scale3(short x, short y, short z) {
short t =   10 * y + z +  y * x ;
return t;
}

Verification:

However, verification failed, the given assembly codes seems to be wrong. It should have long as parameter type instead of short

1
$ gcc -Og -S scale3.c && ./wash.py scale3.s && cat clean_scale3.s
1
2
3
4
5
scale3:
	leal	10(%rdi), %eax  	# %eax = 10 + x
	imull	%eax, %esi			# %esi = (10 + x) * y
	leal	(%rsi,%rdx), %eax	# %eax = (10 + x) * y + z
	ret
1
$ gcc -O1 -S scale3.c && ./wash.py scale3.s && cat clean_scale3.s
1
2
3
4
5
6
scale3:
	leaq	(%rsi,%rsi,4), %rax  # %rax = 5y
	leaq	(%rdx,%rax,2), %rax	 # %rax = 10y + z
	imulq	%rdi, %rsi			 # %rsi = x*y
	addq	%rsi, %rax			 # %rax = 10y + z + x*y
	ret

3.5.2 Unary and Binary Operations

Unary Operation

Operations in the second group are unary operations, with the single operand serving as both source and destination.

  • This operand can be either a register or a memory location.
  • For example, the instruction incq (%rsp)
  • This syntax is reminiscent of the C increment ++ and decrement -- operators
Binary Operation

The third group consists of binary operations, where the second operand is used as both a source and a destination.

  • This syntax is reminiscent of the C assignment operators, such as x -= y.
  • Observe, however, that the source operand is given first and the destination second.For example, the instruction subq %rax,%rdx decrements register %rdx by the value in %rax. (It helps to read the instruction as “Subtract %rax from %rdx.”)
  • The first operand can be either an immediate value, a register, or a memory location. The second can be either a register or a memory location. As with the mov instructions, the two operands cannot both be memory locations.

Practice Problem 3.8

Assume the following values are stored at the indicated memory addresses and registers:

1
2
3
4
5
Address 	Value 	Register 	Value
0x100 		0xFF 	%rax 		0x100
0x108 		0xAB 	%rcx 		0x1
0x110 		0x13 	%rdx 		0x3
0x118 		0x11

Fill in the following table showing the effects of the following instructions, in terms of both the register or memory location that will be updated and the resulting value:

1
2
3
4
5
6
7
Instruction 			Destination 			Value
addq %rcx,(%rax)		
subq %rdx,8(%rax)
imulq $16,(%rax,%rdx,8)
incq 16(%rax)
decq %rcx
subq %rdx,%rax

My solution : :white_check_mark:

1
2
3
4
5
6
7
Instruction 			Destination 			Value
addq %rcx,(%rax)		Memory at 0x100			0x100
subq %rdx,8(%rax)		Memory at 0x108			0xA8
imulq $16,(%rax,%rdx,8)	Memory at 0x118			0x110
incq 16(%rax)			Memory at 0x110			0x14
decq %rcx				Register %rcx			0x0
subq %rdx,%rax			Register %rax			0xFD

3.5.3 Shift Operations

The final group consists of shift operations, where the shift amount is given first and the value to shift is given second. Both arithmetic and logical right shifts are possible

  • The different shift instructions can specify the shift amount either as an immediate value or with the single-byte register %cl. (These instructions are unusual in only allowing this specific register as the operand.)

  • With x86-64, a shift instruction operating on data values that are w bits long determines the shift amount from the low-order m bits of register %cl, where $m = \log _2 w$. The higher-order bits are ignored.

    So, for example, when register %cl has hexadecimal value 0xFF, then instruction salb would shift by 7, while salw would shift by 15, sall would shift by 31, and salq would shift by 63.

  • sal stands for arithmetic shift left

    shl shand for (logical shift left)

Practice Problem 3.9

Suppose we want to generate assembly code for the following C function:

1
2
3
4
5
6
long shift_left4_rightn(long x, long n)
{
x <<= 4;
x >>= n;
return x;
}

The code that follows is a portion of the assembly code that performs the actual shifts and leaves the final value in register %rax. Two key instructions have been omitted. Parameters x and n are stored in registers %rdi and %rsi, respectively

1
2
3
4
5
6
7
# long shift_left4_rightn(long x, long n)
# x in %rdi, n in %rsi
shift_left4_rightn:
movq %rdi, %rax 	# Get x
_______________		# x <<= 4 
movl %esi, %ecx 	# Get n (4 bytes)
_______________		# x >>= n

Fill in the missing instructions, following the annotations on the right. The right shift should be performed arithmetically.

My solution: :white_check_mark:

1
2
3
4
5
6
7
# long shift_left4_rightn(long x, long n)
# x in %rdi, n in %rsi
shift_left4_rightn:
movq %rdi, %rax 	# Get x
shlq  $4 , %rax		# x <<= 4 
movl %esi, %ecx 	# Get n (4 bytes)
sarq  %cl , %rax		# x >>= n

Verification:

1
gcc -Og -S shift.c && ./wash.py shift.s && cat clean_shift.s
1
2
3
4
5
6
shift_left4_rightn:
	movq	%rdi, %rax
	salq	$4, %rax
	movl	%esi, %ecx
	sarq	%cl, %rax
	ret

It might seem odd to use a movl instruction, given that n is eight bytes long, but keep in mind that only the least significant byte is required to specify the shift amount.

3.5.4 Discussion

compilers generate code that uses individual registers for multiple program values and moves program values among the registers.

Practice Problem 3.10

Consider the following code, in which we have omitted the expression being computed:

1
2
3
4
5
6
7
8
short arith3(short x, short y, short z)
{
short p1 = ?;
short p2 = ?;
short p3 = ?;
short p4 = ?;
return p4;
}

The portion of the generated assembly code implementing these expressions is as follows:

1
2
3
4
5
6
7
8
9
# short arith3(short x, short y, short z)
# x in %rdi, y in %rsi, z in %rdx
arith3:
orq %rsi, %rdx
sarq $9, %rdx
notq %rdx
movq %rsi, %rax
subq %rdx, %rax
ret

Based on this assembly code, fill in the missing portions of the C code

My solution : :white_check_mark:

1
2
3
4
5
6
7
8
9
10
# short arith3(short x, short y, short z)
# x in %rdi, y in %rsi, z in %rdx
# %rdi = x , %rsi = y , %rdx = z
arith3:
orq %rsi, %rdx		# z = z | y
sarq $9, %rdx		# z >>= 9 
notq %rdx			# z = ~z
movq %rsi, %rax		# %rax = y
subq %rdx, %rax		# y -= z
ret					# return y
1
2
3
4
5
6
7
8
short arith3(short x, short y, short z)
{
short p1 = z | y;
short p2 = p1 >> 9;
short p3 = ~p2;
short p4 = y - p3;
return p4;
}

Verification

Again, the give C code should have type long instead of short

1
$ gcc -Og -S arith.c && ./wash.py arith.s && cat clean_arith.s
1
2
3
4
5
6
7
arith3:
	orl		%esi, %edx
	sarw	$9, %dx
	notl	%edx
	movl	%esi, %eax
	subl	%edx, %eax
	ret
1
2
3
4
5
6
7
arith3:
	orq		%rsi, %rdx
	sarq	$9, %rdx
	notq	%rdx
	movq	%rsi, %rax
	subq	%rdx, %rax
	ret

Practice Problem 3.11

It is common to find assembly-code lines of the form

1
xorq %rcx,%rcx

in code that was generated from C where no exclusive-or operations were present.

A. Explain the effect of this particular exclusive-or instruction and what useful operation it implements.

B. What would be the more straightforward way to express this operation in assembly code?

C. Compare the number of bytes to encode any two of these three different implementations of the same operation.

My solution : :warning:

A : According to boolean algebra, $a\oplus a = 0$, so this instruction means clear %rcx

B : movq $0,%rcx

C :

1
$ objdump -d xor.o
1
2
3
4
5
6
7
xor.o:     file format elf64-x86-64

Disassembly of section .text:

0000000000000000 <.text>:
   0:	48 c7 c1 00 00 00 00 	mov    $0x0,%rcx
   7:	48 31 c9             	xor    %rcx,%rcx

The xor version is apparently shorter

Solution on book:

C :

Other ways to set %rcx to zero rely on the property that any instruction that updates the lower 4 bytes will cause the high-order bytes to be set to zero. Thus, we could use either xorl %ecx,%ecx (2 bytes) or movl $0,%ecx (5 bytes).

3.5.5 Special Arithmetic Operations

As we saw in Section 2.3, multiplying two 64-bit signed or unsigned integers can yield a product that requires 128 bits to represent.

The x86-64 instruction set provides limited support for operations involving 128-bit (16-byte) numbers. Continuing with the naming convention of word (2 bytes), double word (4 bytes), and quad word (8 bytes), Intel refers to a 16-byte quantity as an oct word.

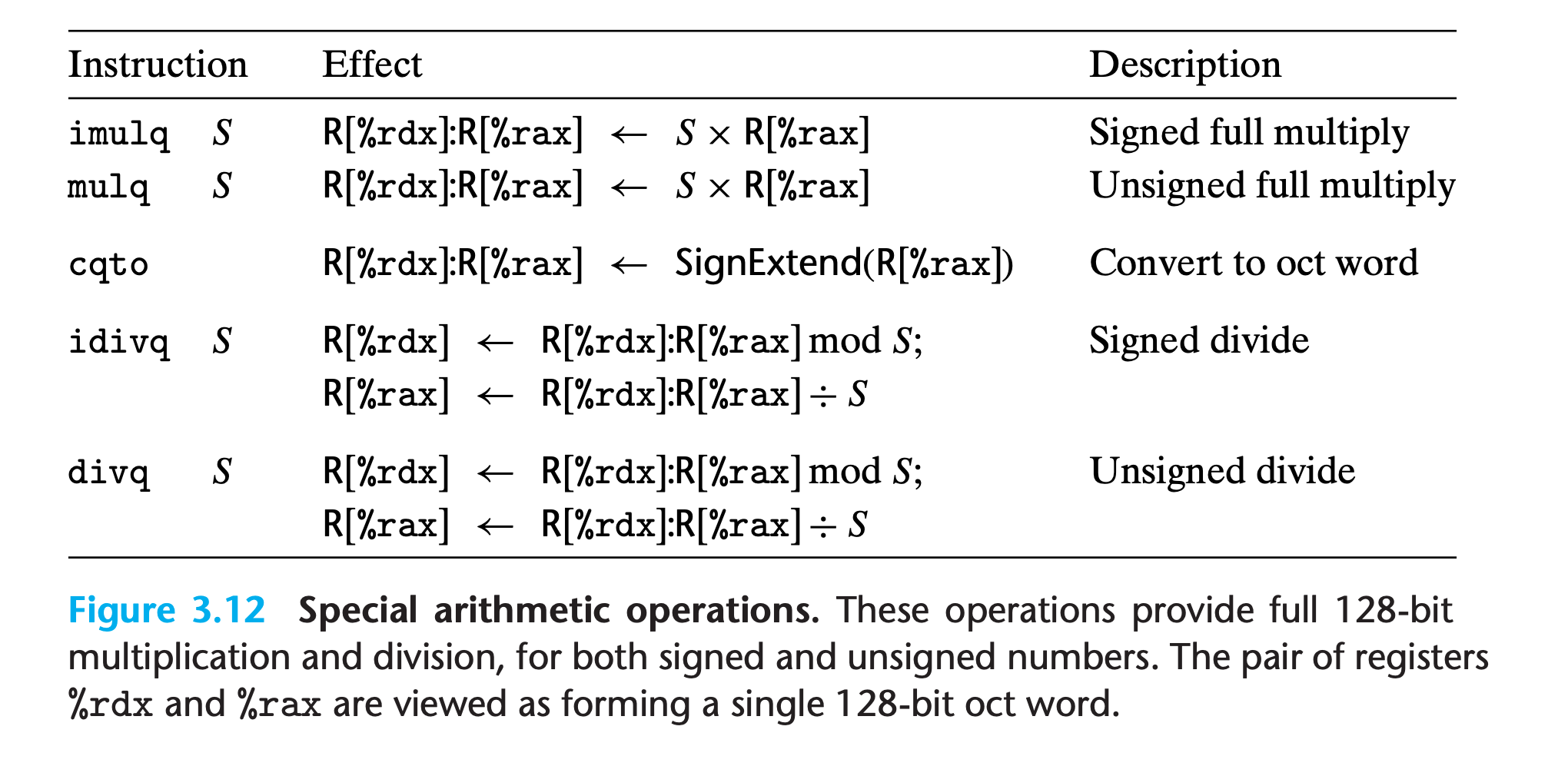
special arithmetic operations

Multiplication instruction class

The imulq instruction has two different forms

  • imulq S,DIn this form, it serves as a “two operand” multiply instruction, generating a 64-bit product from two 64-bit operands.

    • Both unsigned multiply and two’s-complement multiply have the same bit-level behavior, so there is only one instruction.
    • High-order bits in result are truncated

  • imulq S and mulq S Compute the full 128-bit product of two 64-bit values— mulq for unsigned and imulq for two’s-complement

    • For both of these instructions, one argument must be in register %rax, and the other is given as the instruction source operand

    • The product is then stored in registers %rdx (high-order 64 bits) and %rax (low-order 64 bits).

    • Although the name imulq is used for two distinct multiplication operations, the assembler can tell which one is intended by counting the number of operands.

    • Example

      1
      2
      3
      4
      5
      #include <inttypes.h>
      typedef unsigned __int128 uint128_t;
      void store_uprod(uint128_t *dest, uint64_t x, uint64_t y) {
      *dest=x* (uint128_t) y;
      }
      1
      2
      3
      4
      5
      6
      7
      8
      #void store_uprod(uint128_t *dest, uint64_t x, uint64_t y)
      #dest in %rdi, x in %rsi, y in %rdx
      store_uprod:
       movq %rsi, %rax 		#Copy x to multiplicand
       mulq %rdx 				#Multiply by y
       movq %rax, (%rdi) 		#Store lower 8 bytes at dest
       movq %rdx, 8(%rdi) 	#Store upper 8 bytes at dest+8
       ret
      Division instruction class

division and modulus operations are provided by the singleoperand divide instructions similar to the single-operand multiply instructions.

  • The signed division instruction idivl takes as its dividend the 128-bit quantity in registers %rdx (high-order 64 bits) and %rax (low-order 64 bits). The divisor is given as the instruction operand.

  • The instruction stores the quotient in register %rax and the remainder in register %rdx.

  • Usually, the dividend is given as a 64-bit value. This value should be stored in register %rax. The bits of %rdx should then be set to either all zeros (unsigned arithmetic) or the sign bit of %rax (signed arithmetic).

    The latter operation can be performed using the instruction cqto. This instruction takes no operands—it implicitly reads the sign bit from %rax and copies it across all of %rdx.

  • Example

    1
    2
    3
    4
    5
    6
    void remdiv(long x, long y,long *qp, long *rp) {
    	long q = x/y;
    	long r = x%y;
    	*qp = q;
    	*rp = r;
    }
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    # void remdiv(long x, long y, long *qp, long *rp)
    # x in %rdi, y in %rsi, qp in %rdx, rp in %rcx
    remdiv:
      movq %rdx, %r8 	# Copy qp, %rdx is required for the division operation
      movq %rdi, %rax 	# Move x to lower 8 bytes of dividend
      cqto 				# Sign-extend to upper 8 bytes of dividend
      idivq %rsi 		# Divide by y
      movq %rax, (%r8) 	# Store quotient at qp
      movq %rdx, (%rcx) # Store remainder at rp
      ret

  • idivq for signed, divq for unsigned, the processes are the same.

Practice Problem 3.12

Consider the following function for computing the quotient and remainder of two unsigned 64-bit numbers:

1
2
3
4
5
6
7
void uremdiv(unsigned long x, unsigned long y,
unsigned long *qp, unsigned long *rp) {
unsigned long q = x/y;
unsigned long r = x%y;
*qp = q;
*rp = r;
}

Modify the assembly code shown for signed division to implement this function

My solution : :white_check_mark:

1
2
3
4
5
6
7
8
9
10
# void uremdiv(unsigned long x, unsigned long y, unsigned long *qp, unsigned long *rp)
# x in %rdi, y in %rsi, qp in %rdx, rp in %rcx
uremdiv:
  movq %rdx, %r8 	# Copy qp, %rdx is required for the division operation
  movq %rdi, %rax 	# Move x to lower 8 bytes of dividend
  xorl %edx, %edx	# clear %rdx
  divq %rsi 		# Divide by y
  movq %rax, (%r8) 	# Store quotient at qp
  movq %rdx, (%rcx) # Store remainder at rp
  ret

Verification:

1
$ gcc -O2 -S uremdiv.c && ./wash.py uremdiv.s && cat uremdiv.s
1
2
3
4
5
6
7
8
uremdiv:
	movq	%rdi, %rax
	movq	%rdx, %rdi
	xorl	%edx, %edx
	divq	%rsi
	movq	%rax, (%rdi)
	movq	%rdx, (%rcx)
	ret

Solution on the book :

(compiled with -O1)

1
2
3
4
5
6
7
8
9
10
#void uremdiv(unsigned long x, unsigned long y, unsigned long *qp, unsigned long *rp)
#x in %rdi, y in %rsi, qp in %rdx, rp in %rcx
 uremdiv:
 movq %rdx, %r8 	#Copy qp
 movq %rdi, %rax 	#Move x to lower 8 bytes of dividend
 movl $0, %edx 		#Set upper 8 bytes of dividend to 0
 divq %rsi 			#Divide by y
 movq %rax, (%r8) 	#Store quotient at qp
 movq %rdx, (%rcx) 	#Store remainder at rp
 ret

Tips

  • When converting a function to assembly code, %rdi always gets the first argument, %rsi gets the second one.