3.7 Procedures
Procedures are a key abstraction in software. They provide a way to package code that implements some functionality with a designated set of arguments and an optional return value.
Procedures come in many guises in different programming languages—functions, methods, subroutines, handlers, and so on—but they all share a general set of features
suppose procedure P calls procedure Q, and Q then executes and returns back to P. These actions involve one or more of the following mechanisms:
- Passing control. The program counter must be set to the starting address of the code for Q upon entry and then set to the instruction in P following the call to Q upon return.
- Passing data. P must be able to provide one or more parameters to Q, and Q must be able to return a value back to P.
- Allocating and deallocating memory. Q may need to allocate space for local variables when it begins and then free that storage before it returns.
3.7.1 The Run-Time Stack
A key feature of the procedure-calling mechanism of C, and of most other languages, is that it can make use of the last-in, first-out memory management discipline provided by a stack data structure
As P calls Q, control and data information are added to the end of the stack. This information gets deallocated when P returns.
When an x86-64 procedure requires storage beyond what it can hold in registers, it allocates space on the stack. This region is referred to as the procedure’s stack frame
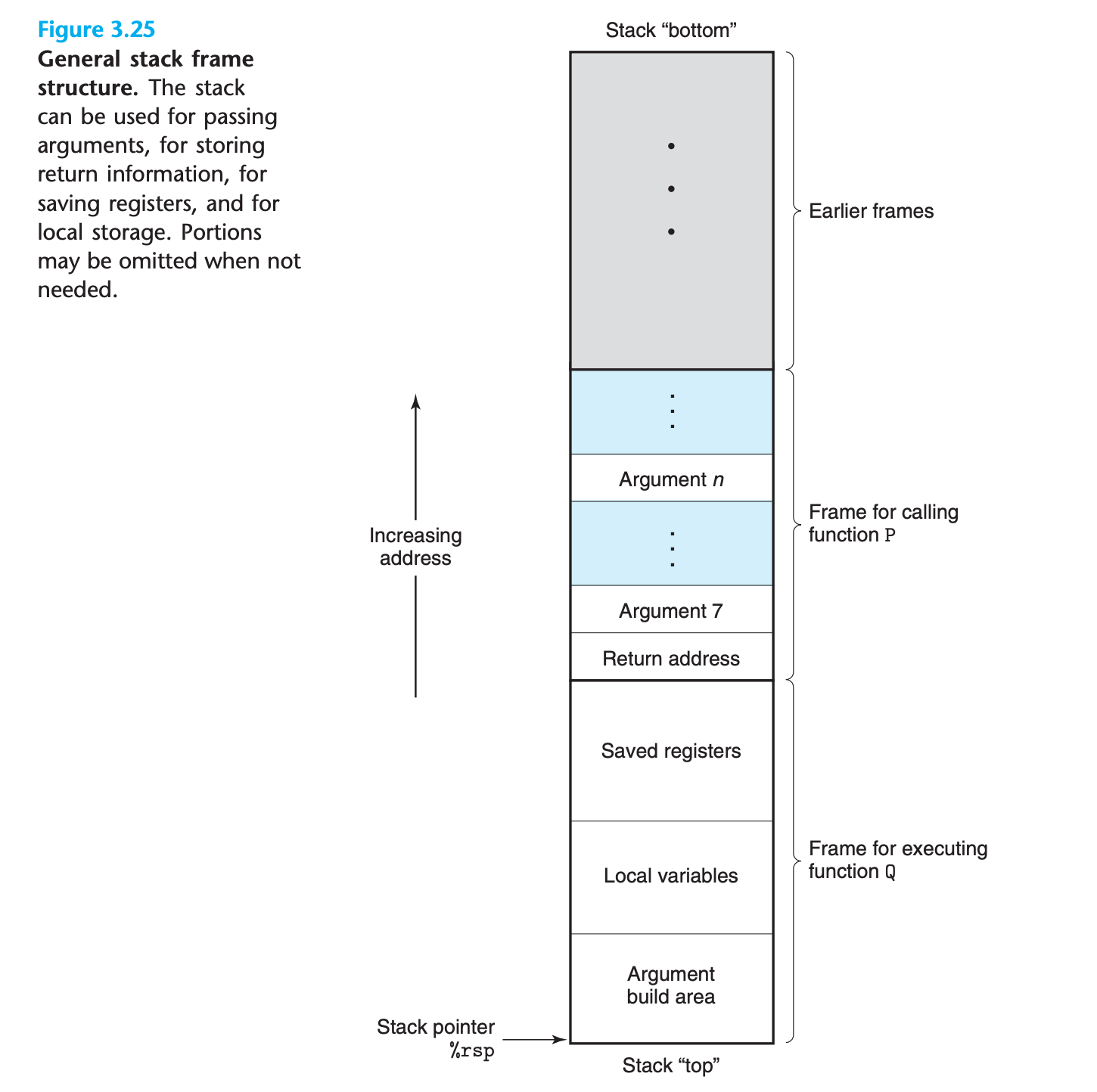
The frame for the currently executing procedure is always at the top of the stack.
When procedure P calls procedure Q, it will push the return address onto the stack, indicating where within P the program should resume execution once Q returns. We consider the return address to be part of P’s stack frame, since it holds state relevant to P.
The stack frames for most procedures are of fixed size, allocated at the beginning of the procedure. Some procedures, however, require variable-size frames. This issue is discussed in Section 3.10.5.
many procedures have six or fewer arguments, and so all of their parameters can be passed in registers. Thus the “argument build area” can be omitted.
If more than 6 arguments are required, they can be stored by calling procedure within its stack frame prior to the call.
many functions do not even require a stack frame. This occurs when all of the local variables can be held in registers and the function does not call any other functions (sometimes referred to as a leaf procedure, in reference to the tree structure of procedure calls).
3.7.2 Control Transfer
Passing control from function P to function Q involves simply setting the program counter (PC) to the starting address of the code for Q
However, when it later comes time for Q to return, the processor must have some record of the code location where it should resume the execution of P.
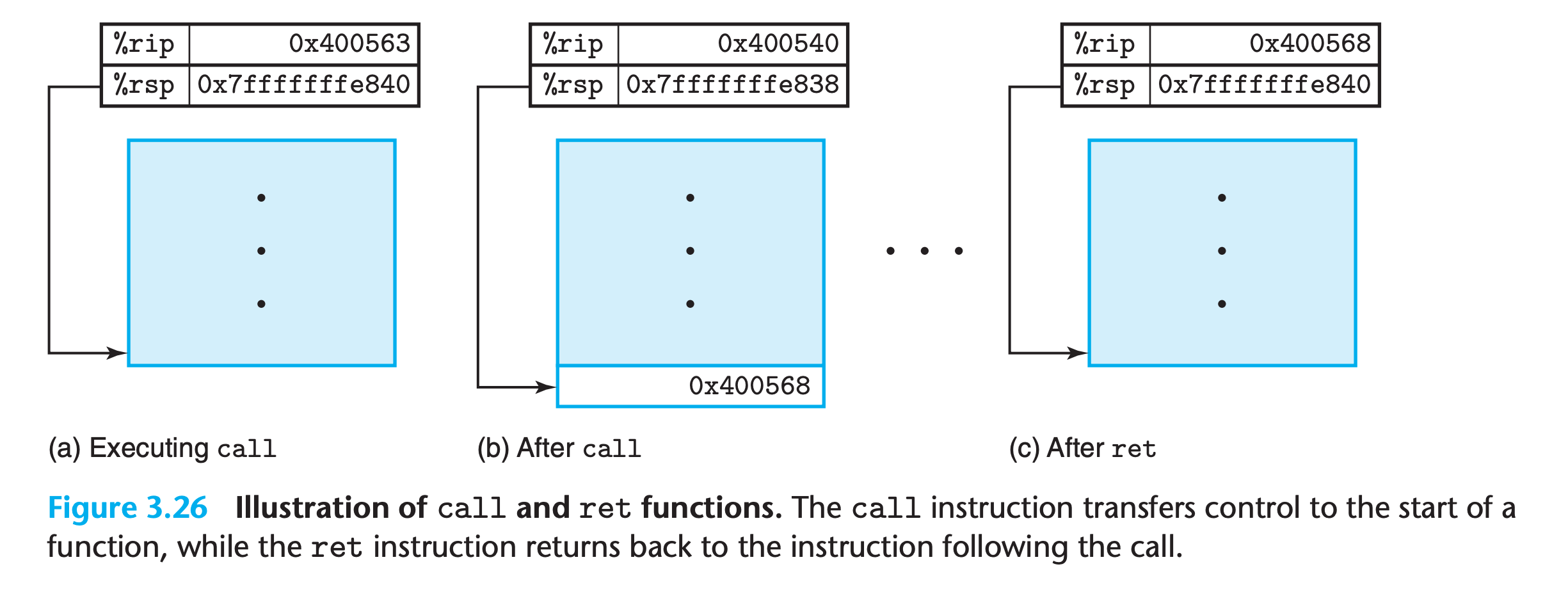
call instruction pushes an address A onto the stack and sets the PC to the beginning of Q. The pushed address A is referred to as the return address and is computed as the address of the instruction immediately following the call instruction.
The counterpart instruction ret pops an address A off the stack and sets the PC to A
1 | call Lable # direct procedure call |
1 | #Beginning of function multstore |
- The effect of the
callis- push the return address 0x400568 onto the stack
- jump to the first instruction in function multstore, at address 0x0400540
- The effect of the
retis- pops the value 0x400568 from the stack and jumps to this address, resuming the execution of main just after the call instruction
Practice Problem 3.32
The disassembled code for two functions
firstandlastis shown below, along with the code for a call of first by functionmain:
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# u in %rdi, v in %rsi
0000000000400540 <last>:
400540: 48 89 f8 mov %rdi,%rax #L1: u
400543: 48 0f af c6 imul %rsi,%rax #L2: u*v
400547: c3 retq #L3: Return
# Disassembly of last(long x)
# x in %rdi
0000000000400548 <first>:
400548: 48 8d 77 01 lea 0x1(%rdi),%rsi #F1: x+1
40054c: 48 83 ef 01 sub $0x1,%rdi #F2: x-1
400550: e8 eb ff ff ff callq 400540 <last> #F3: Call last(x-1,x+1)
400555: f3 c3 repz retq #F4: Return
....
<main>:
400560: e8 e3 ff ff ff callq 400548 <first>#M1: Call first(10)
400565: 48 89 c2 mov %rax,%rdx #M2: ResumeEach of these instructions is given a label. Starting with the calling of
first(10)bymain, fill in the following table to trace instruction execution through to the point where the program returns back tomain.
Label PC Instruction %rdi%rsi%rax%rsp*%rspDescription M1 0x400560 callq10 X X 0x7fffffffe820 X Call first(10)F1 F2 F3 L1 L2 L3 F4 M2
My solution : :white_check_mark:
| Label | PC | Instruction | %rdi |
%rsi |
%rax |
%rsp |
*%rsp |
Description |
|---|---|---|---|---|---|---|---|---|
| M1 | 0x400560 | callq |
10 | X | X | 0x7fffffffe820 | X | Call first(10) |
| F1 | 0x400548 | lea |
10 | X | X | 0x7fffffffe818 | 0x400565 | x + 1 |
| F2 | 0x40054c | sub |
10 | 11 | X | 0x7fffffffe818 | 0x400565 | x - 1 |
| F3 | 0x400550 | callq |
9 | 11 | X | 0x7fffffffe818 | 0x400565 | Call last(x-1,x+1) |
| L1 | 0x400540 | mov |
9 | 11 | X | 0x7fffffffe810 | 0x400555 | u |
| L2 | 0x400543 | imul |
9 | 11 | 9 | 0x7fffffffe810 | 0x400555 | u*v |
| L3 | 0x400547 | retq |
9 | 11 | 99 | 0x7fffffffe810 | 0x400555 | Return |
| F4 | 0x400555 | repz retq |
9 | 11 | 99 | 0x7fffffffe818 | 0x400565 | Return |
| M2 | 0x400565 | mov |
9 | 11 | 99 | 0x7fffffffe820 | X | Resume |
3.7.3 Data Transfer
procedure calls may involve passing data as arguments, and returning from a procedure may also involve returning a value
With x86-64, most of these data passing to and from procedures take place via registers.
With x86-64, up to six integral (i.e., integer and pointer) arguments can be passed via registers.
They are used in a specified order.
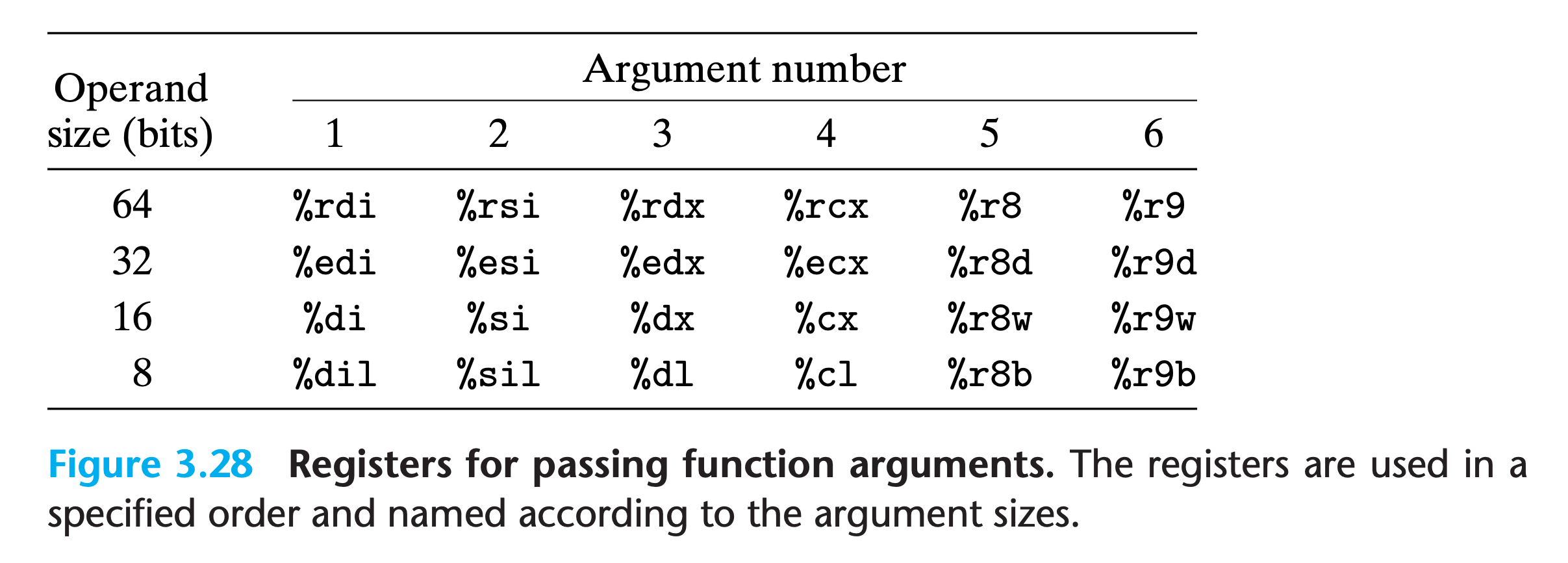
When a function has more than six integral arguments, the other ones are passed on the stack.
The order of arguments are reversed, as shown in figure 3.25
1
2
3
4
5
6
7
8
9
10
11
12
13
14int fun(int a1 , int a2 , int a3 , int a4 , int a5 , int a6 , int a7 , int a8 , int a9 );
//When calling fun
rdi = a1;
rsi = a2;
rdx = a3;
rcx = a4;
r8 = a5;
r9 = a6;
|-------stack-------|
| ...... |
|_________a9________|
|_________a8________|
|_________a7________|
|_____resume addr___|
When passing parameters on the stack, all data sizes are rounded up to be multiples of eight.
Example
1
2
3
4
5
6
7
8void proc(long a1, long *a1p,int a2, int *a2p,
short a3, short *a3p,char a4, char *a4p)
{
*a1p += a1;
*a2p += a2;
*a3p += a3;
*a4p += a4;
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19/*
Arguments passed as follows:
a1 in %rdi (64 bits)
a1p in %rsi (64 bits)
a2 in %edx (32 bits)
a2p in %rcx (64 bits)
a3 in %r8w (16 bits)
a3p in %r9 (64 bits)
a4 at %rsp+8 ( 8 bits)
a4p at %rsp+16 (64 bits)
*/
proc:
movq 16(%rsp), %rax
addq %rdi, (%rsi)
addl %edx, (%rcx)
addw %r8w, (%r9)
movl 8(%rsp), %edx
addb %dl, (%rax)
ret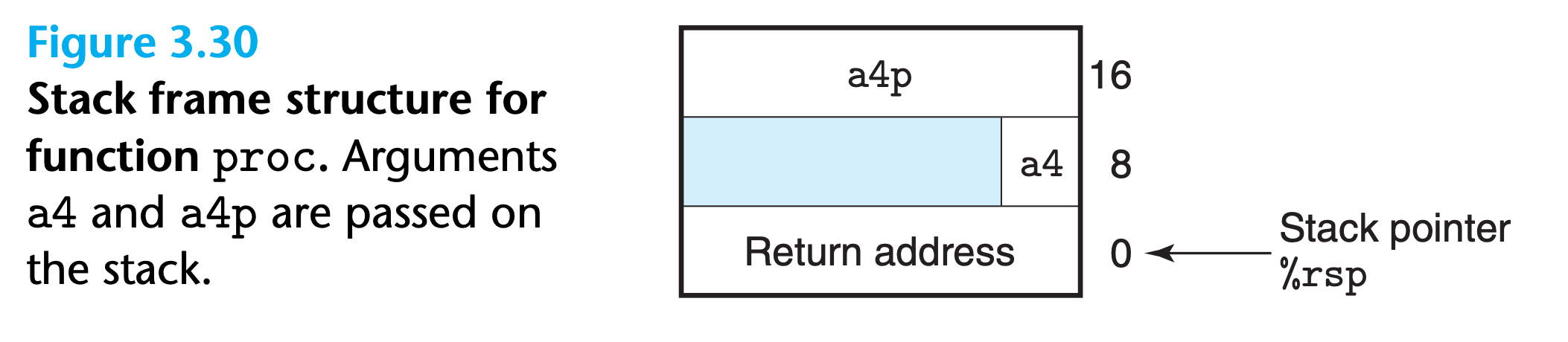
Practice Problem 3.33
A C function
procprobhas four argumentsu, a, v, andb. Each is either a signed number or a pointer to a signed number, where the numbers have different sizes. The function has the following body
2
3
*v += b;
return sizeof(a) + sizeof(b);It compiles to the following x86-64 code:
2
3
4
5
6
movslq %edi, %rdi
addq %rdi, (%rdx)
addb %sil, (%rcx)
movl $6, %eax
retDetermine a valid ordering and types of the four parameters. There are two correct answers
My solution : :x:
1 | procprob: |
addb %sil,(%rcx) just use %rsi‘s lower-order byte, so type of the second argument is unknown!
Solution on the book:
Let us first describe one answer and then explain the second possibility. If we assume the first addition (line 3) implements *u += a, while the second (line 4) implements *v += b, then we can see that a was passed as the first argument in %edi and converted from 4 bytes to 8 before adding it to the 8 bytes pointed to by %rdx. This implies that a must be of type int and u must be of type long *. We can also see that the low-order byte of argument b is added to the byte pointed to by %rcx. This implies that v must be of type char *, but the type of b is ambiguous—it could be 1, 2, 4, or 8 bytes long. This ambiguity is resolved by noting the return value of 6, computed as the sum of the sizes of a and b. Since we know a is 4 bytes long, we can deduce that b must be 2.
1 | int procprobl(int a, short b, long *u, char *v) |
Alternatively, we can see that the same assembly code would be valid if the two sums were computed in the assembly code in the opposite ordering as they are in the C code. This would result in interchanging arguments a and b and arguments u and v, yielding the following prototype:
1 | int procprob(int b, short a, long *v, char *u); |
3.7.4 Local Storage on the Stack
Typically, a procedure allocates space on the stack frame by decrementing the stack pointer. This results in the portion of the stack frame labeled “Local variables” in Figure 3.25.


As shown in Figure 3.30, arguments 7 and 8 are now at offsets 8 and 16 relative to the stack pointer, because the return address was pushed onto the stack.
3.7.5 Local Storage in Registers
Although only one procedure can be active at a given time, we must make sure that when one procedure (the caller) calls another (the callee), the callee does not overwrite some register value that the caller planned to use later.
By convention, registers
%rbx, %rbp, and%r12–%r15are classified as callee-saved registers. When procedure P calls procedure Q, Q must preserve the values of these registers, ensuring that they have the same values when Q returns to P as they did when Q was called.Procedure Q can preserve a register value by either not changing it at all or by pushing the original value on the stack, altering it, and then popping the old value from the stack before returning
(The pushing of register values has the effect of creating the portion of the stack frame labeled “Saved registers” in Figure 3.25)(They are in Q’s frame, it is Q’s responsibility to save them!)
All other registers, except for the stack pointer
%rsp, are classified as caller-saved registers. This means that they can be modified by any function- Q can use these register freely
- It is incumbent upon P (the caller) to first save the data(move data from caller-saved to callee-saved ) before it makes the call.
As an example, consider the function P shown in Figure 3.34(a). It calls Q twice. During the first call, it must retain the value of x for use later. Similarly, during the second call, it must retain the value computed for Q(y).
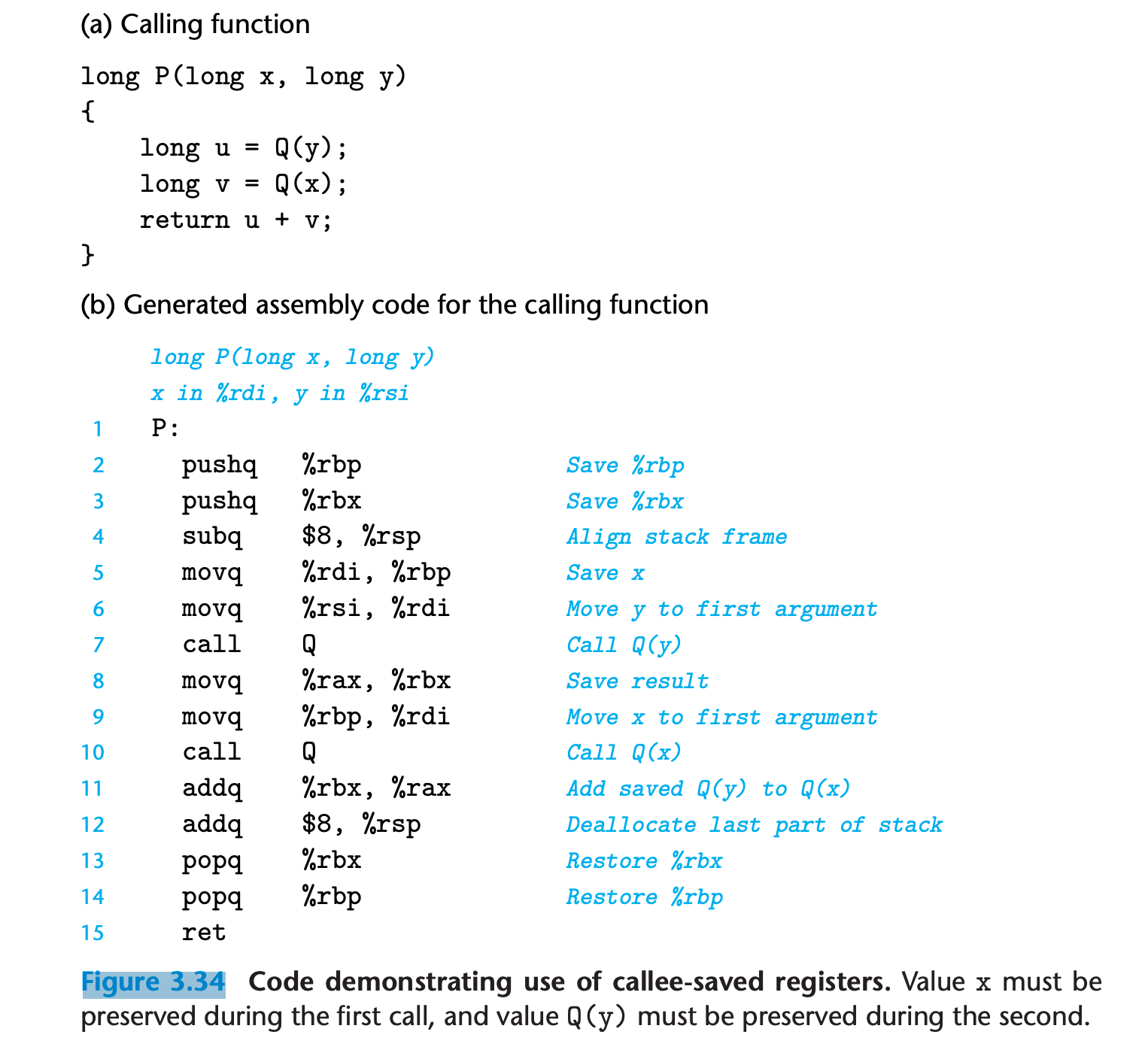
- Note how they are popped in the reverse order from how they were pushed, to account for the last-in, first-out discipline of a stack.
- what the purpose of
subq $8,%rspandaddq $8, %rspwithout using%rspat all ? answer- In order to align stack frame to $2^4=16$, 4 is gcc’s default value, this can be specified by
-mpreferred-stack-boundary=n - In this example, 8 bytes already for P’s return address, so P should allocate $16 -8 = 8$ bytes more.
- In order to align stack frame to $2^4=16$, 4 is gcc’s default value, this can be specified by
Practice Problem 3.34
Consider a function P, which generates local values, named
a0–a8. It then calls function Q using these generated values as arguments. Gcc produces the following code for the first part of P:
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# x in %rdi
P:
pushq %r15
pushq %r14
pushq %r13
pushq %r12
pushq %rbp
pushq %rbx
subq $24, %rsp
movq %rdi, %rbx
leaq 1(%rdi), %r15
leaq 2(%rdi), %r14
leaq 3(%rdi), %r13
leaq 4(%rdi), %r12
leaq 5(%rdi), %rbp
leaq 6(%rdi), %rax
movq %rax, (%rsp)
leaq 7(%rdi), %rdx
movq %rdx, 8(%rsp)
movl $0, %eax
call Q
...A. Identify which local values get stored in callee-saved registers.
B. Identify which local values get stored on the stack.
C. Explain why the program could not store all of the local values in callee-saved registers.
My solution : :white_check_mark:
1 | subq $24, %rsp # 16 bytes for save local value, 8 bytes for alignment to 2^4 |
3.7.6 Recursive Procedures
The conventions we have described for using the registers and the stack allow x86-64 procedures to call themselves recursively
This method of implementing function calls and returns even works for more complex patterns, including mutual recursion (e.g., when procedure P calls Q, which in turn calls P).

Practice Problem 3.35
For a C function having the general structure
2
3
4
5
6
7
if ( _____ )
return _______;
unsigned long nx = __________;
long rv = rfun(nx);
return __________;
}gcc generates the following assembly code:
2
3
4
5
6
7
8
9
10
11
12
13
testq %rdi, %rdi
jne .L8
movl $0, %eax
ret
.L8:
pushq %rbx
movq %rdi, %rbx
shrq $2, %rdi
call rfun
addq %rbx, %rax
popq %rbx
retA. What value does
rfunstore in the callee-saved register%rbx?B. Fill in the missing expressions in the C code shown above.
My solution: :white_check_mark:
1 | # long rfun(unsigned long x) |
1 | long rfun(unsigned long x) { |
3.8 Array Allocation and Access
Arrays in C are one means of aggregating scalar data into larger data types. C uses a particularly simple implementation of arrays, and hence the translation into machine code is fairly straightforward
3.8.1 Basic Principles
For data type T and integer constant N
1 | T A [N]; |
The declaration has two effects.
it allocates a contiguous region of $L \times N$ bytes in memory, where L is the size (in bytes) of data type T.
It introduces an identifier
Athat can be used as a pointer to the beginning of the array.Array element i will be stored at address $A + L \times i$
The memory referencing instructions of x86-64 are designed to simplify array access.
For example, suppose E is an array of values of type int and we wish to evaluate E[i], where the address of E is stored in register %rdx and i is stored in register %rcx. Then the instruction
1 | movl (%rdx,%rcx,4),%eax |
will perform the address computation E + 4*i, read that memory location, and copy the result to register %eax. The allowed scaling factors of 1, 2, 4, and 8 cover the sizes of the common primitive data types.
Practice Problem 3.36
Consider the following declarations:
2
3
4
5
short Q[2];
int **R[9];
double *S[10];
short *T[2];Fill in the following table describing the element size, the total size, and the address of element i for each of these arrays.
Array Element size Total size Start address Element i P Q R S T
My solution : :white_check_mark:
| Array | Element size | Total size | Start address | Element i |
|---|---|---|---|---|
| P | 4 | 20 | $x_p$ | $x_p + 4 \times i$ |
| Q | 2 | 4 | $x_q$ | $x_q + 2 \times i$ |
| R | 8 | 72 | $x_r$ | $x_r + 8 \times i$ |
| S | 8 | 80 | $x_s$ | $x_s + 8 \times i$ |
| T | 8 | 16 | $x_t$ | $x_t + 8 \times i$ |
3.8.2 Pointer Arithmetic
C allows arithmetic on pointers, where the computed value is scaled according to the size of the data type referenced by the pointer.
That is, if p is a pointer to data of type T , and the value of p is $x_p$, then the expression p+i has value $x_p + L \times i$, where L is the size of data type T .
The array subscripting operation can be applied to both arrays and pointers. The array reference A[i] is identical to the expression *(A+i).

- The final example shows that one can compute the difference of two pointers within the same data structure, with the result being data having type long and value equal to the difference of the two addresses divided by the size of the data type.
Note that &a will make a pointer with type a.
1 |
|
Example
1 | int array [10] ; |
Practice Problem 3.37
Suppose $x_P$, the address of short integer array P, and long integer index i are stored in registers
%rdxand%rcx, respectively. For each of the following expressions, give its type, a formula for its value, and an assembly-code implementation. The result should be stored in register%raxif it is a pointer and register element%axif it has data typeshort.
Expression Type Value Assembly code P[1]P+3+iP[i * 6 - 5]P[2]&P[i + 2]
My solution: :white_check_mark:
| Expression | Type | Value | Assembly code |
|---|---|---|---|
P[1] |
short |
$M[x_P + 2]$ | movw 2(%rdx),%ax |
P+3+i |
short* |
$x_P + (3+i) \times 2$ | leaq 6(%rdx,%rcx,2), %rax |
P[i * 6 - 5] |
short |
$M[ x_P + (i\times 6 - 5)\times 2]$ | |
P[2] |
short |
$M[x_P + 2\times 2]$ | movw 4(%rdx),%ax |
&P[i + 2] |
short* |
$x_P + (i+2) \times 2$ | leaq 4(%rdx,%rcx,2),%rax |
1 | # P[i*6 -5] |
3.8.3 Nested Arrays
The general principles of array allocation and referencing hold even when we create arrays of arrays
1 | int A[5][3]; |
- Data type
row3_tis defined to be an array of three integers - Array A contains five such elements, each requiring 12 bytes to store the three integers. The total array size is then $4 \times 5 \times 3 = 60$ bytes.
The array elements are ordered in memory in row-major order, meaning all elements of row 0, which can be written A[0], followed by all elements of row 1 (A[1]), and so on

This ordering is a consequence of our nested declaration. Viewing A as an array of five elements, each of which is an array of three int’s, we first have A[0], followed by A[1], and so on.
For an array declared as T D[R][C];
$$
&D[i][j] = D + L\times(C \times i + j)
$$
Programming languages or their standard libraries that support multi-dimensional arrays typically have a native row-major or column-major storage order for these arrays.
Row-major order is used in C/C++/Objective-C (for C-style arrays), PL/I,[4] Pascal,[5] Speakeasy,[*citation needed*] SAS,[6] and Rasdaman.[7]
Column-major order is used in Fortran, MATLAB,[8] GNU Octave, S-Plus,[9] R,[10] Julia,[11] and Scilab.[12]
So there is no way to declare a “column major” array in C
Practice Problem 3.38
Consider the following source code, where M and N are constants declared with
2
3
4
5
6
7
long P[M][N];
long Q[N][M];
long sum_element(long i, long j) {
return P[i][j] + Q[j][i];
}In compiling this program, gcc generates the following assembly code:
2
3
4
5
6
7
8
9
10
11
12
13
#i in %rdi, j in %rsi
sum_element:
leaq 0(,%rdi,8), %rdx
subq %rdi, %rdx
addq %rsi, %rdx
leaq (%rsi,%rsi,4), %rax
addq %rax, %rdi
leaq Q(%rip), %rax
movq (%rax,%rdi,8), %rax
leaq P(%rip), %rcx
addq (%rcx,%rdx,8), %rax
retUse your reverse engineering skills to determine the values of M and N based on this assembly code.
My solution: :white_check_mark:
1 | #long sum_element(long i, long j) |
1 | return P[i][j] + Q[j][i]; |
Test
1 |
|
1 | traversal1: |
Even without optimization, gcc generate almost the same code for traversal1 and traversal2, the difference in time consuming do not show in machine level code. They have much to do with the cache mechanism.
3.8.4 Fixed-Size Arrays
The C compiler is able to make many optimizations for code operating on multidimensional arrays of fixed size.

Practice Problem 3.40
The following C code sets the diagonal elements of one of our fixed-size arrays to val:
2
3
4
5
6
7
8
typedef int fix_matrix[N][N];
/* Set all diagonal elements to val */
void fix_set_diag(fix_matrix A, int val) {
long i;
for (i = 0; i < N; i++)
A[i][i] = val;
}When compiled with optimization level -O1, gcc generates the following assembly code:
2
3
4
5
6
7
8
9
movq %rdi, %rax
addq $1088, %rdi
.L2:
movl %esi, (%rax)
addq $68, %rax
cmpq %rdi, %rax
jne .L2
rep retCreate a C code program
fix_set_diag_optthat uses optimizations similar to those in the assembly code, in the same style as the code in Figure 3.37(b). Use expressions involving the parameter N rather than integer constants, so that your code will work correctly if N is redefined.
My solution :
1 | fix_set_diag: |
1 |
|
1 | $ diff my.s test.s |
Solution on the book:
1 | /* Set all diagonal elements to val */ |
3.8.5 Variable-Size Arrays
Historically, C only supported multidimensional arrays where the sizes (with the possible exception of the first dimension) could be determined at compile time.
Programmers requiring variable-size arrays had to allocate storage for these arrays using functions such as
mallocorcalloc, and they had to explicitly encode the mapping of multidimensional arrays into single-dimension ones via row-major indexingISO C99 introduced the capability of having array dimension expressions that are computed as the array is being allocated.
1
2
3
4int n ;
scanf("%d" , &n);
int array [n];
//These codes will compile without errorint A[expr1][expr2].The dimensions of the array are determined by evaluating the expressions expr1 and expr2 at the time the declaration is encountered.For example
1
2
3
4//The parameter n must precede the parameter A[n][n], so that the function can compute the array dimensions as the parameter is encountered.
int var_ele(long n, int A[n][n], long i, long j) {
return A[i][j];
}1
2
3
4
5
6
7
8
#int var_ele(long n, int A[n][n], long i, long j)
#n in %rdi, A in %rsi, i in %rdx, j in %rcx
var_ele:
imulq %rdx, %rdi #Compute n*i
leaq (%rsi,%rdi,4), %rax #Compute A + 4(n*i)
movl (%rax,%rcx,4), %eax #Read from M[xA + 4(n*i) + 4j ]
retThe dynamic version must use a multiplication instruction to scale i by n, rather than a series of shifts and adds. In some processors, this multiplication can incur a significant performance penalty, but it is unavoidable in this case.
When variable-size arrays are referenced within a loop, the compiler can often optimize the index computations by exploiting the regularity of the access patterns.
Example
1
2
3
4
5
6
7
8
9
10/* Compute i,k of variable matrix product */
int var_prod_ele(long n, int A[n][n], int B[n][n], long i, long k) {
long j;
int result = 0;
for (j = 0; j < n; j++)
result += A[i][j] * B[j][k];
return result;
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23# compiled with -O1
var_prod_ele:
testq %rdi, %rdi # if(n<=0) return 0;
jle .L4
salq $2, %rcx # %rcx = 4*i
imulq %rdi, %rcx # %rcx = 4*i * n
addq %rcx, %rsi # %rsi = A + 4*i * n
leaq 0(,%rdi,4), %r9 # %r9 = 4*n
leaq (%rdx,%r8,4), %r8 # %r8 = B + 4*k
movl $0, %edx # %rdx = 0 //j = 0
movl $0, %eax # %rax = 0
.L3:
movl (%rsi,%rdx,4), %ecx # %rax = A[i * n + j]
imull (%r8), %ecx # %rcx = B[k]*A[i*n + j]
addl %ecx, %eax # res += %rcx
addq $1, %rdx # j++
addq %r9, %r8 # %r8 = B + 4*k + 4*n
cmpq %rdx, %rdi # if(n == j) break
jne .L3 # else continue
rep ret
.L4:
movl $0, %eax
ret1
2
3
4
5
6
7
8
9
10
11
12int var_prod_ele(long n, int A[n][n], int B[n][n], long i, long k){
if(n<=0) return 0;
int j = 0;
int res = 0;
int * start_A = &A[i][j];
int * start_B = &B[j][k];
do{
res += (*(start_A+j)) * (*start_B + n*j);
j++;
}while(j != n);
return res;
}Whether
gccgenerates the pointer-based code of Figure 3.37(b) or the array-based code of Figure 3.38(b), these optimizations will significantly improve program performance.
3.9 Heterogeneous Data Structures
C provides two mechanisms for creating data types by combining objects of different types:
structaggregate multiple objects into a single unitunionallow an object to be referenced using several different types.
3.9.1 Structures
The implementation of structures is similar to that of arrays in that all of the components of a structure are stored in a contiguous region of memory and a pointer to a structure is the address of its first byte
The compiler maintains information about each structure type indicating the byte offset of each field.
For example
1 | struct rec { |

To access the fields of a structure, the compiler generates code that adds the appropriate offset to the address of the structure.
1 | struct rec * r ; |
1 | # Registers: r in %rdi |
1 | int * ptr = &(r->a[1]); |
1 | leaq 8(%rdi,%rsi,4), %rax #Set %rax to &r->a[i],r in %rdi, i %rsi |
As these examples show, the selection of the different fields of a structure is handled completely at compile time. The machine code contains no information about the field declarations or the names of the fields, only offset.
Practice Problem 3.41 :white_check_mark:
Consider the following structure declaration:
2
3
4
5
6
7
8
short *p;
struct {
short x;
short y;
} s;
struct test *next;
};This declaration illustrates that one structure can be embedded within another, just as arrays can be embedded within structures and arrays can be embedded within arrays.
The following procedure (with some expressions omitted) operates on this structure:
2
3
4
5
st->s.y = ______;
st->p = ______;
st->next = _______;
}A. What are the offsets (in bytes) of the following fields?
B. How many total bytes does the structure require?
C. The compiler generates the following assembly code for
st_init:
2
3
4
5
6
7
movzwl 8(%rdi), %eax
movw %ax, 10(%rdi)
leaq 10(%rdi), %rax
movq %rax, (%rdi)
movq %rdi, 16(%rdi)
retOn the basis of this information, fill in the missing expressions in the code for
st_init.
1 | //A |
Perhaps the compiler pads some space to align with the max size in the struct, that is align to 8.
gcc gives that sizeof(test) == 24
Practice Problem 3.42
The following code shows the declaration of a structure of type
ACEand the prototype for a functiontest:
2
3
4
5
short v;
struct ACE *p;
};
short test(struct ACE *ptr);gcc generates the following assembly code:
2
3
4
5
6
7
8
9
10
movl $1, %eax
jmp .L2
.L3:
imulw (%rdi), %ax
movq 8(%rdi), %rdi
.L2:
testq %rdi, %rdi
jne .L3
rep retA. Use your reverse engineering skills to write C code for test.
B. Describe the data structure that this structure implements and the operation performed by test.
My solution: :white_check_mark:
1 | short test(struct ACE *ptr){ |
3.9.2 Unions
Unions provide a way to circumvent the type system of C, allowing a single object to be referenced according to multiple types.
- The syntax of a union declaration is identical to that for structures
- Rather than having the different fields reference different blocks of memory, they all reference the same block.
- the overall size of a union equals the maximum size of any of its fields.
Usage of unions
Unions can be useful in several contexts. However, they can also lead to nasty bugs, since they bypass the safety provided by the C type system
the use of two different fields in a data structure will be mutually exclusive.
Then, declaring these two fields as part of a union rather than a structure will reduce the total space allocated
For example, suppose we want to implement a binary tree data structure where each leaf node has two double data values and each internal node has pointers to two children but no data.
if we declare the node as
1
2
3
4
5struct node_s {
struct node_s *left;
struct node_s *right;
double data[2];
};then every node requires 32 bytes, with half the bytes wasted for each type of node.
if we declare the node as
1
2
3
4
5
6
7union node_u {
struct {
union node_u *left;
union node_u *right;
} internal;
double data[2];
};then every node will require just 16 bytes
However, there is no way to determine whether a given node is a leaf or an internal node.
A common method is to introduce an enumerated type defining the different possible choices for the union, and then create a structure containing a tag field and the union:
1
2
3
4
5
6
7
8
9
10
11typedef enum { N_LEAF, N_INTERNAL } nodetype_t;
struct node_t {
nodetype_t type;
union {
struct {
struct node_t *left;
struct node_t *right;
} internal;
double data[2];
} info;
};This structure requires a total of 24 bytes: 4 for type, and either 8 each for info.internal.left and info.internal.right or 16 for info.data(additional 4 bytes for padding)
In this case, the savings gain of using a union is small relative to the awkwardness of the resulting code. For data structures with more fields, the savings can be more compelling.
Unions can also be used to access the bit patterns of different data types
For example, suppose we use a function to convert a value
dof typedoubleto a valueuof typeunsigned long:1
2
3
4
5
6
7
8unsigned long double2bits(double d) {
union {
double d;
unsigned long u;
} temp;
temp.d = d;
return temp.u;
};In this code, we store the argument in the union using one data type and access it using another
When using unions to combine data types of different sizes, byte-ordering issues can become important.
For example, suppose we write a procedure that will create an 8-byte double using the bit patterns given by two 4-byte unsigned values:
1
2
3
4
5
6
7
8
9
10double uu2double(unsigned word0, unsigned word1)
{
union {
double d;
unsigned u[2];
} temp;
temp.u[0] = word0;
temp.u[1] = word1;
return temp.d;
}On a little-endian machine, such as an x86-64 processor, argument word0 will become the low-order 4 bytes of d, while word1 will become the high-order 4 bytes
Practice Problem 3.43
Suppose you are given the job of checking that a C compiler generates the proper code for structure and union access. You write the following structure declaration:
2
3
4
5
6
7
8
9
10
11
struct {
long u;
short v;
char w;
} t1;
struct {
int a[2];
char *p;
} t2;
} u_type;You write a series of functions of the form
2
3
*dest = expr;
}with different access expressions expr and with destination data type type set according to type associated with expr. You then examine the code generated when compiling the functions to see if they match your expectations.
Suppose in these functions that
upanddestare loaded into registers%rdiand%rsi, respectively. Fill in the following table with data type type and sequences of one to three instructions to compute the expression and store the result at dest.
2
3
4
5
6
7
8
9
10
11
12
up->t1.u long movq (%rdi), %rax
movq %rax, (%rsi)
up->t1.v
&up->t1.w
up->t2.a
up->t2.a[up->t1.u]
*up->t2.p
My solution : :warning:
1 | /* |
in get3 gcc generate leaq 10(%rdi),%rax rather then add 12 to %rdi, indicating my padding strategy might be wrong.
char ‘s address need to be multiple of 1, that is, any value.
1 | /* |
3.9.3 Data Alignment
Many computer systems place restrictions on the allowable addresses for the primitive data types, requiring that the address for some objects must be a multiple of some value K (typically 2, 4, or 8)
For example, suppose a processor always fetches 8 bytes from memory with an address that must be a multiple of 8. If we can guarantee that any double will be aligned to have its address be a multiple of 8, then the value can be read or written with a single memory operation. Otherwise, we may need to perform two memory accesses, since the object might be split across two 8-byte memory blocks.
The x86-64 hardware will work correctly regardless of the alignment of data
However, Intel recommends that data be aligned to improve memory system performance
Their alignment rule is based on the principle that any primitive object of K bytes must have an address that is a multiple of K.
1
2
3
4
5K Types
1 char
2 short
4 int, float
8 long, double, char *The compiler places directives in the assembly code indicating the desired alignment for global data.
1
.align 8
This ensures that the data following it will start with an address that is a multiple of 8
For code involving structures, the compiler may need to insert gaps in the field allocation to ensure that each structure element satisfies its alignment requirement.
For example
1
2
3
4
5
6
7
8
9struct S1 {
int i;
char c;
int j;
};
/*
0 4 5 9
i____c_j____
*/This won’t satisfy the align principle. Instead, the compiler inserts a 3-byte gap between fields
candj:1
20 4 8 12
i____c_000j____In addition, the compiler may need to add padding to the end of the structure so that each element in an array of structures will satisfy its alignment requirement.
For example
1
2
3
4
5struct S2 {
int i;
int j;
char c;
};If we pack this structure into 9 bytes, we can still satisfy the alignment requirements, but the next element in the array won’t stick to the requirement.
1
20 4 8 9
i____j____c_ i____....So the compiler pads
S2to 12 bytes, adding 3 bytes 0 at the end.
Practice Problem 3.44
For each of the following structure declarations, determine the offset of each field, the total size of the structure, and its alignment requirement for x86-64:
2
3
4
5
B. struct P2 { int i[2]; char c[8]; short s[4]; long *j; };
C. struct P3 { long w[2]; int *c[2] };
D. struct P4 { char w[16]; char *c[2] };
E. struct P5 { struct P4 a[2]; struct P1 t };
My solution : :white_check_mark:
1 | //A |
Verification:
1 | struct P1 { short i; int c; int *j; short *d; }; |
1 | access: |
Practice Problem 3.45
Answer the following for the structure declaration
2
3
4
5
6
7
8
9
10
int *a;
float b;
char c;
short d;
long e;
double f;
int g;
char *h;
} rec;A. What are the byte offsets of all the fields in the structure?
B. What is the total size of the structure?
C. Rearrange the fields of the structure to minimize wasted space, and then show the byte offsets and total size for the rearranged structure.
My solution : :white_check_mark:
1 | 0 8 12 14 16 24 32 40 |
After rearrangement
1 | struct { |
Can’t decrease the size any more.
Verification:
1 | typedef struct { |
1 | $ gcc -Og test.c && ./a.out |