csapp

Ch3PartIV

3.10 Combining Control and Data in Machine-Level Programs

In this section, we look at ways in which data and control interact with each other.

3.10.1 Understanding Pointers

Pointers are a central feature of the C programming language

  • Every pointer has an associated type.

    • For example

      1
      2
      3
      int data ;
      int * p = &data;
      int** pp = &p;

    • The special void * type represents a generic pointer. It can be converted to other type.

      1
      int * p = (int*)malloc(sizeof(int));

  • Every pointer has a value.This value is an address of some object of the designated type.

    • The special NULL (0) value indicates that the pointer does not point anywhere.

  • Pointers are created with the & operator. In machine code lea is often used

  • Pointers are dereferenced with the * operator. Dereferencing is implemented by a memory reference, either storing to or retrieving from the specified address.

  • Arrays and pointers are closely related.

    • The name of an array can be referenced (but not updated) as if it were a pointer variable

  • Casting from one type of pointer to another changes its type but not its value.

    • One effect of casting is to change any scaling of pointer arithmetic

    • For example

      1
      2
      3
      4
      5
      6
      7
      char string [20] = {0};
      char * p2c = string ;
      int * p2i = (int*)p2c;
      string[12] = 'A';
      printf("p2c : %p , p2i : %p\n" , p2c ,p2i);
      printf("%p:%c\n" , (p2c+12) , *(p2c+12));
      printf("%p:%c\n" , (p2i + 3) , *(p2i + 3));

  • Pointers can also point to functions

    • This provides a powerful capability for storing and passing references to code, which can be invoked in some other part of the program.

    • For example

      1
      2
      3
      4
      5
      int fun(int x, int *p);
      int (*fp)(int, int *);
      fp = fun;
      int y = 1;
      int result = fp(3, &y);

      The value of a function pointer is the address of the first instruction in the machine-code representation of the function.

3.10.2 Life in the Real World: Using the gdb Debugger

The GNU debugger gdb provides a number of useful features to support the run-time evaluation and analysis of machine-level programs

  • It is very helpful to first run objdump to get a disassembled version of the program.
  • The general scheme is to set breakpoints near points of interest in the program.
  • gdb has an obscure command syntax, but the online help information (invoked within gdb with the help command) overcomes this shortcoming.
  • Rather than using the command-line interface to gdb, many programmers prefer using ddd, an extension to gdb that provides a graphical user interface.

gdb commands

tutorial from csapp student site

gdb manual

man gdb

3.10.3 Out-of-Bounds Memory References and Buffer Overflow

We have seen that C does not perform any bounds checking for array references, and that local variables are stored on the stack along with state information such as saved register values and return addresses. This combination can lead to serious program errors, where the state stored on the stack gets corrupted by a write to an out-of-bounds array element. When the program then tries to reload the register or execute a ret instruction with this corrupted state, things can go seriously wrong.

A particularly common source of state corruption is known as buffer overflow

For example, gets in the standard library

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/* Implementation of library function gets() */
/* gets() has been removed from stdio.h since C11 !!! */
char *gets(char *s)
{
int c;
char *dest = s;
while ((c = getchar()) != ’\n’ && c != EOF)
*dest++ = c;
if (c == EOF && dest == s)
/* No characters read */
return NULL;
*dest++ = ’\0’; /* Terminate string */
return s;
}

/* Read input line and write it back */
void echo()
{
char buf[8]; /* Way too small! */
gets(buf);
puts(buf);
}
1
$ gcc -Og -S -fno-stact-protector -mpreferred-stack-boundary=3 test.c
1
2
3
4
5
6
7
8
9
10
11
12
echo:
	pushq	%rbx		# save previous sp
	subq	$8, %rsp	# allocat 8 bytes for array buf	
	movq	%rsp, %rbx	# save current sp
	movq	%rbx, %rdi	# pass buf to gets function
	movl	$0, %eax
	call	gets@PLT
	movq	%rbx, %rdi	# pass buf to puts function
	call	puts@PLT
	addq	$8, %rsp	# deallocate the space
	popq	%rbx		# restore previous sp
	ret

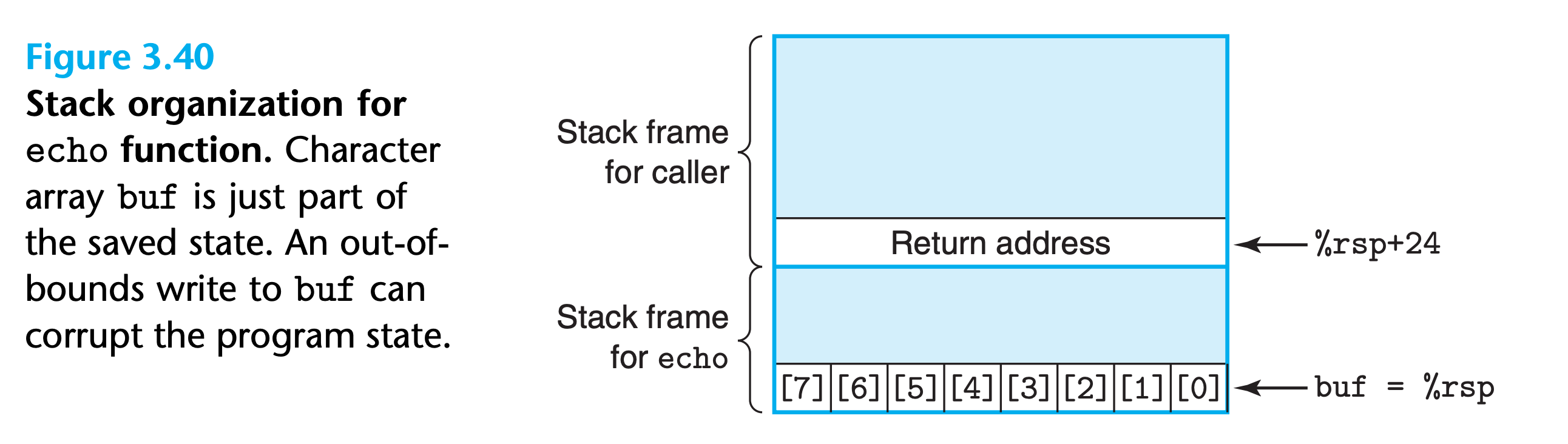
stack status

(Return address is %rsp+8 in my case)

Since C do not check array referrence, we can input string longer than 7 to corrupt the return address

A better version involves using the function fgets, which includes as an argument a count on the maximum number of bytes to read.

a number of commonly used library functions, including strcpy, strcat, and sprintf, have the property that they can generate a byte sequence without being given any indication of the size of the destination buffer. Such conditions can lead to vulnerabilities to buffer overflow !!!

Practice Problem 3.46

Following codes shows a (low-quality) implementation of a function that reads a line from standard input, copies the string to newly allocated storage, and returns a pointer to the result.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/* This is very low-quality code.
It is intended to illustrate bad programming practices.
See Practice Problem 3.46. */
#include <stdlib.h>
#include <string.h>
#include <stdio.h>
char *gets(char *s)
{
int c;
char *dest = s;
while ((c = getchar()) != '\n' && c != EOF)
*dest++ = c;
if (c == EOF && dest == s)
/* No characters read */
return NULL;
*dest++ = '\0'; /* Terminate string */
return s;
}
char *get_line()
{
char buf[4];
char *result;
gets(buf);
result = malloc(strlen(buf));
strcpy(result, buf);
return result;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
get_line:
	pushq	%rbp
	pushq	%rbx
	subq	$24, %rsp
	leaq	12(%rsp), %rbx
	movq	%rbx, %rdi
	call	gets
	movq	$-1, %rcx
	movl	$0, %eax
	movq	%rbx, %rdi
	repnz scasb
	movq	%rcx, %rdx
	notq	%rdx
	leaq	-1(%rdx), %rdi
	call	malloc@PLT
	movq	%rbx, %rsi
	movq	%rax, %rdi
	call	strcpy@PLT
	addq	$24, %rsp
	popq	%rbx
	popq	%rbp
	ret

Consider the following scenario. Procedure get_line is called with the return address equal to 0x400776 and register %rbx equal to 0x0123456789ABCDEF. You type in the string “0123456789012345678901234”

The program terminates with a segmentation fault. You run gdb and determine that the error occurs during the execution of the ret instruction of get_line

A. Fill in the diagram that follows, indicating as much as you can about the stack just after executing the instruction at line 3 in the disassembly. Label the quantities stored on the stack (e.g., “Return address”) on the right, and their hexadecimal values (if known) within the box. Each box represents 8 bytes. Indicate the position of %rsp. Recall that the ASCII codes for characters 0–9 are 0x30–0x39.

1
2
3
4
5
|00 00 00 00 00 40 07 76| Return address
|                       |
|                       |
|                       |
|                       |

B. Modify your diagram to show the effect of the call to gets .

C. To what address does the program attempt to return?

D. What register(s) have corrupted value(s) when get_line returns?

E. Besides the potential for buffer overflow, what two other things are wrong with the code for get_line?

My solution:

play it with gdb, there’s lots of fun.

send raw bytes to program or gdb

1
2
gdb> r < <(python -c "print '0000000000000000000000000000}HUUUU\x00\x00\x6bHUUUU'")
# input as file
1
2
3
4
gdb> r <<< $(python -c "print '0000000000000000000000000000}HUUUU\x00\x00\x1bHUUUU'")
# input as variable
# This one doesn't work with bash version newer than 4.4
# /bin/bash: warning: command substitution: ignored null byte in input
1
$ echo -e '0000000000000000000000000000}HUUUU\x00\x00\x1bHUUUU' | ./prog

Examine stack

1
gdb>x/64bx $rsp

Start with gui mode

1
$ gdb -tui prog

Why it won’t work outside of gdb ?

more info

gdb messes with your environment variables, and could disable ASLR. Most likely, starting gdb and running ‘unset env LINES’ and ‘unset env COLUMNS’ before throwing your shellcode will make the output line up with execution outside gdb. :)

Also, don’t forget to turn off the ASLR !!!

1
2
3
4
# disable
$ echo 0 | sudo tee /proc/sys/kernel/randomize_va_space
# enable
$ echo 2 | sudo tee /proc/sys/kernel/randomize_va_space

How to keep the shell

Why system(‘/bin/sh’) doesn’t work

compile with -Og or not spawn shell in debugger or not spawn shell outside debugger or not
No pwndbg:Yes(align 16 needed, ret in ROP) Yes
vanilla gdb :NO Yes
gdb-peda:Yes Yes
gdb-gef:NO Yes
Yes pwndbg:Yes(align 16 needed, ret in ROP) Yes
vanilla gdb:NO Yes
gdb-peda:Yes Yes
gdb-gef:NO Yes

Change pwndbg assembly flavor : set disassembly-flavor att

However, code browsing like vanilla gdb is still impossible in pwndbg

gdb-peda and gdb-gef don’t support this, too.

Typically, the program is fed with a string that contains the byte encoding of some executable code, called the exploit code, plus some extra bytes that overwrite the return address with a pointer to the exploit code. The effect of executing the ret instruction is then to jump to the exploit code.

  • In one form of attack, the exploit code then uses a system call to start up a shell program, providing the attacker with a range of operating system functions.
  • In another form, the exploit code performs some otherwise unauthorized task, repairs the damage to the stack, and then executes ret a second time, causing an (apparently) normal return to the caller.
Programming tips

Any interface to the external environment should be made “bulletproof” so that no behavior by an external agent can cause the system to misbehave.

3.10.4 Thwarting Buffer Overflow Attacks

Buffer overflow attacks have become so pervasive and have caused so many problems with computer systems that modern compilers and operating systems have implemented mechanisms to make it more difficult to mount these attacks and to limit the ways by which an intruder can seize control of a system via a buffer overflow attack.

Stack Randomization

In order to insert exploit code into a system, the attacker needs to inject both the code as well as a pointer to this code as part of the attack string. This requires knowing the stack address where the string will be located.

  • Historically, the stack addresses for a program were highly predictable. For all systems running the same combination of program and operating system version, the stack locations were fairly stable across many machines.

  • The idea of stack randomization is to make the position of the stack vary from one run of a program to another

    • This is implemented by allocating a random amount of space between 0 and n bytes on the stack at the start of a program, for example, by using the allocation function alloca, which allocates space for a specified number of bytes on the stack.
    • This allocated space is not used by the program, but it causes all subsequent stack locations to vary from one execution of a program to another.
    • The allocation range n needs to be large enough to get sufficient variations in the stack addresses, yet small enough that it does not waste too much space in the program

  • a simple way to determine a “typical” stack address

    1
    2
    3
    4
    5
    int main() {
    long local;
    printf("local at %p\n", &local);
    return 0;
    }
    • Running the code 10,000 times on a Linux machine in 32-bit mode, the addresses ranged from 0xff7fc59c to 0xffffd09c, a range of around $2^{23}.$ Running in 64- bit mode on the newer machine, the addresses ranged from 0x7fff0001b698 to 0x7ffffffaa4a8, a range of nearly $2^{32}$.

  • Stack randomization has become part of ASLR

    With ASLR, different parts of the program, including program code, library code, stack, global variables, and heap data, are loaded into different regions of memory each time a program is run.

  • Overall, however, a persistent attacker can overcome randomization by brute force, repeatedly attempting attacks with different addresses.

    • A common trick is to include a long sequence of nop instructions before the actual exploit code, aka “nop sled”
    • If we set up a 256-byte nop sled, then the randomization over n = $2^{23}$ can be cracked by enumerating $2^{15}$ = 32,768 starting addresses, which is entirely feasible for a determined attacker.

Practice Problem 3.47

Running our stack-checking code 10,000 times on a system running Linux version 2.6.16, we obtained addresses ranging from a minimum of 0xffffb754 to a maximum of 0xffffd754.

A. What is the approximate range of addresses?

B. If we attempted a buffer overrun with a 128-byte nop sled, about how many attempts would it take to test all starting addresses?

My solution : :white_check_mark:

1
2
apprange = math.log(0xffffd754 - 0xffffb754 , 2 )
# 13

The approximate range of address is $2^{13}$

1
2
attemps = (0xffffd754 - 0xffffb754) / 128
# 64

It would take 64 attemps

Solution on the book:

A 128-byte nop sled would cover $2^7$ addresses with each test, and so we would only require around $2^6$ = 64 attempts.

This example clearly shows that the degree of randomization in this version of Linux would provide only minimal deterrence against an overflow attack.

Stack Corruption Detection

In C, there is no reliable way to prevent writing beyond the bounds of an array. Instead, the program can attempt to detect when such a write has occurred before it can have any harmful effects.

  • The idea is to store a special canary value4 in the stack frame between any local buffer and the rest of the stack state

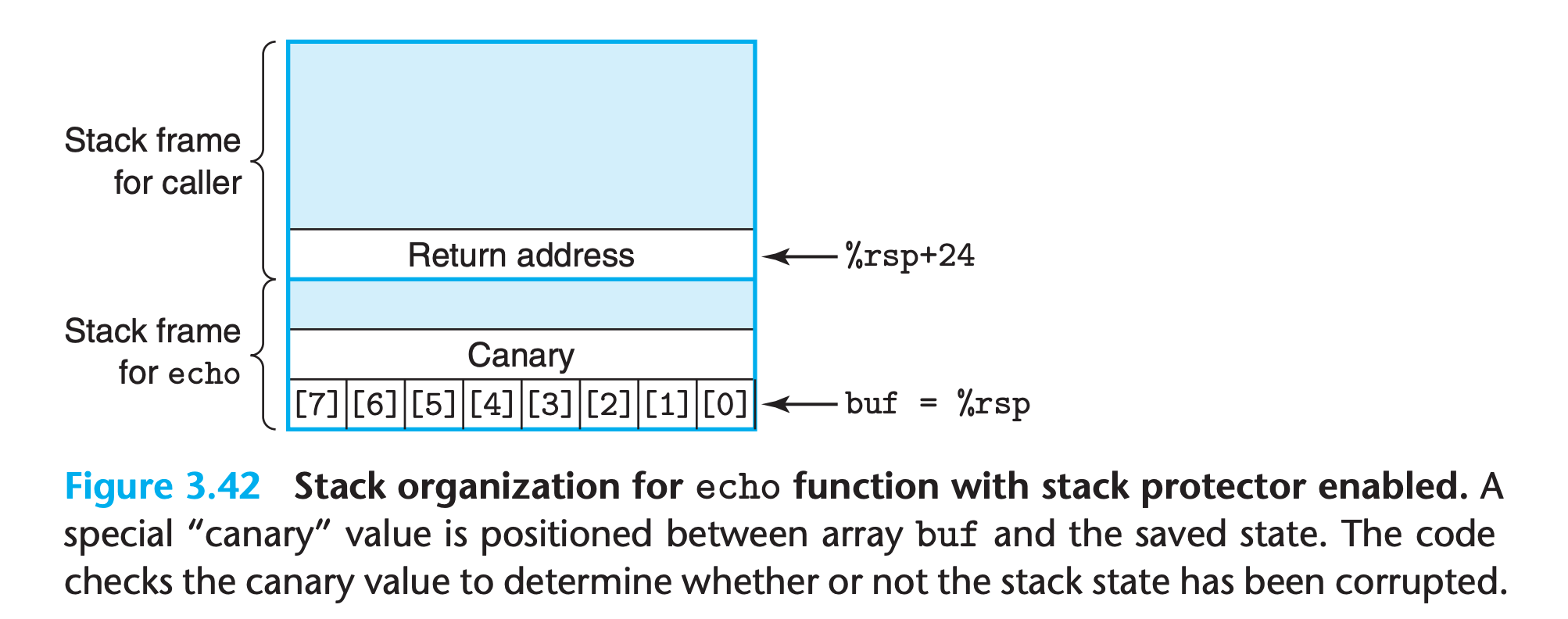
    canary value

  • This canary value, also referred to as a guard value, is generated randomly each time the program runs, and so there is no easy way for an attacker to determine what it is.

  • Before restoring the register state and returning from the function, the program checks if the canary has been altered by some operation of this function or one that it has called. If so, the program aborts with an error.

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    main:
    	subq	$24, %rsp
    	movq	%fs:40, %rax		# get canary value and store it in %rax
    	movq	%rax, 8(%rsp)		# store canary value after return addr
    	xorl	%eax, %eax
    	movl	$0, 4(%rsp)
    	leaq	4(%rsp), %rdx
    	leaq	.LC0(%rip), %rsi
    	movl	$1, %edi
    	call	__printf_chk@PLT
    	movq	8(%rsp), %rcx		# get canary value from stack
    	xorq	%fs:40, %rcx		# check if was modified
    	jne	.L4
    	movl	$0, %eax
    	addq	$24, %rsp
    	ret
    	call	__stack_chk_fail@PLT # if check failed, abort execution

    The instruction argument %fs:40 is an indication that the canary value is read from memory using segmented addressing, an addressing mechanism that dates back to the 80286 and is seldom found in programs running on modern systems.

    By storing the canary in a special segment, it can be marked as “read only,” so that an attacker cannot overwrite the stored canary value.

Practice Problem 3.48

The functions intlen, len, and iptoa provide a very convoluted way to compute the number of decimal digits required to represent an integer. We will use this as a way to study some aspects of the gcc stack protector facility.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int len(char *s) {
return strlen(s);
}
void iptoa(char *s, long *p) {
long val = *p;
sprintf(s, "%ld", val);
}
int intlen(long x) {
long v;
char buf[12];
v = x;
iptoa(buf, &v);
return len(buf);
}

The following show portions of the code for intlen, compiled both with and without stack protector:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# with stack protection on
intlen:
	pushq	%rbx
	subq	$32, %rsp
	movq	%fs:40, %rax
	movq	%rax, 24(%rsp)
	xorl	%eax, %eax
	movq	%rdi, (%rsp)
	movq	%rsp, %rsi
	leaq	12(%rsp), %rbx
	movq	%rbx, %rdi
	call	iptoa
	movq	%rbx, %rdi
	call	len
	movq	24(%rsp), %rdx
	xorq	%fs:40, %rdx
	jne	.L7
	addq	$32, %rsp
	popq	%rbx
	ret
	call	__stack_chk_fail@PLT
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# with stack protection off
intlen:
	pushq	%rbx
	subq	$32, %rsp
	movq	%rdi, 24(%rsp)
	leaq	24(%rsp), %rsi
	leaq	12(%rsp), %rbx
	movq	%rbx, %rdi
	call	iptoa
	movq	%rbx, %rdi
	call	len
	addq	$32, %rsp
	popq	%rbx
	ret

A. For both versions: What are the positions in the stack frame for buf, v, and (when present) the canary value?

B. How does the rearranged ordering of the local variables in the protected code provide greater security against a buffer overrun attack?

My solution : :warning:

A:

1
2
3
4
5
6
7
# protected version:
buf : leaq 12(%rsp)
v	: leaq (%rsp)
canary value : leaq 24(%rsp)
# unprotected version:
buf : leaq 12(%rsp)
v	: 24(%rsp)

B:

the canary value is just above the buf, providing a boundary check

Solution on the book:

B:

In the protected code, local variable v is positioned closer to the top of the stack than buf, and so an overrun of buf will not corrupt the value of v.

Limiting Executable Code Regions

A final step is to eliminate the ability of an attacker to insert executable code into a system. One method is to limit which memory regions hold executable code

  • The hardware supports different forms of memory protection, indicating the forms of access allowed by both user programs and the operating system kernel.

  • Many systems allow control over three forms of access: r w x

    Historically, the x86 architecture merged the read and execute access controls into a single 1-bit flag, so that any page marked as readable was also executable.

  • The stack had to be kept both readable and writable, and therefore the bytes on the stack were also executable.

    • Various schemes were implemented to be able to limit some pages to being readable but not executable, but these generally introduced significant inefficiencies.

  • More recently, AMD introduced an NX (for “no-execute”) bit into the memory protection for its 64-bit processors, separating the read and execute access modes, and Intel followed suit.

    • With this feature, the stack can be marked as being readable and writable, but not executable
    • And the checking of whether a page is executable is performed in hardware, with no penalty in efficiency

  • However, “just-in-time” compilation techniques dynamically generate code for programs written in interpreted languages. So whether or not the run-time system can restrict the executable code to just that part generated by the compiler in creating the original program depends on the language and the operating system.

  • We can control it with -z execstack or -z noexecstack link options.

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    $ pwn checksec can
        Arch:     amd64-64-little
        RELRO:    Full RELRO
        Stack:    Canary found
        NX:       NX disabled
        PIE:      PIE enabled
        RWX:      Has RWX segments
    $ pwn checksec cannot
        Arch:     amd64-64-little
        RELRO:    Full RELRO
        Stack:    Canary found
        NX:       NX enabled
        PIE:      PIE enabled

    3.10.5 Supporting Variable-Size Stack Frames

Usually, the compiler can allocate stack space for a function in compiling stage. Some functions, however, require a variable amount of local storage.

This can occur, for example, when the function calls alloca or declare an array with variable size

To manage a variable-size stack frame, x86-64 code uses register %rbp to serve as a frame pointer (sometimes referred to as a base pointer, and hence the letters bp in %rbp).

For example

1
2
3
4
5
6
7
8
long vframe(long n, long idx, long *q) {
long i;
long *p[n];
p[0] = &i;
for (i = 1; i < n; i++)
p[i] = q;
return *p[idx];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
vframe:
	pushq	%rbp			# save previous stack
	movq	%rsp, %rbp		# make rbp point to current stack frame
	subq	$16, %rsp		# allocate 16 bytes , s1
	leaq	22(,%rdi,8), %rax	
	andq	$-16, %rax
	subq	%rax, %rsp		# s2
	leaq	7(%rsp), %rax
	shrq	$3, %rax
	leaq	0(,%rax,8), %r8	# p
	movq	%r8, %rcx
	leaq	-8(%rbp), %r9	# r9 = &i
	movq	%r9, 0(,%rax,8)	# p[0] = &i;
	movq	$1, -8(%rbp)	# i = 1
	jmp	.L2
.L3:
	movq	%rdx, (%rcx,%rax,8) #*(p+i*8)=q
	addq	$1, -8(%rbp)	#i++
.L2:
	movq	-8(%rbp), %rax	#rax=i
	cmpq	%rax, %rdi #while(n>i)
	jg	.L3
	movq	(%r8,%rsi,8), %rax
	movq	(%rax), %rax
	leave
	ret

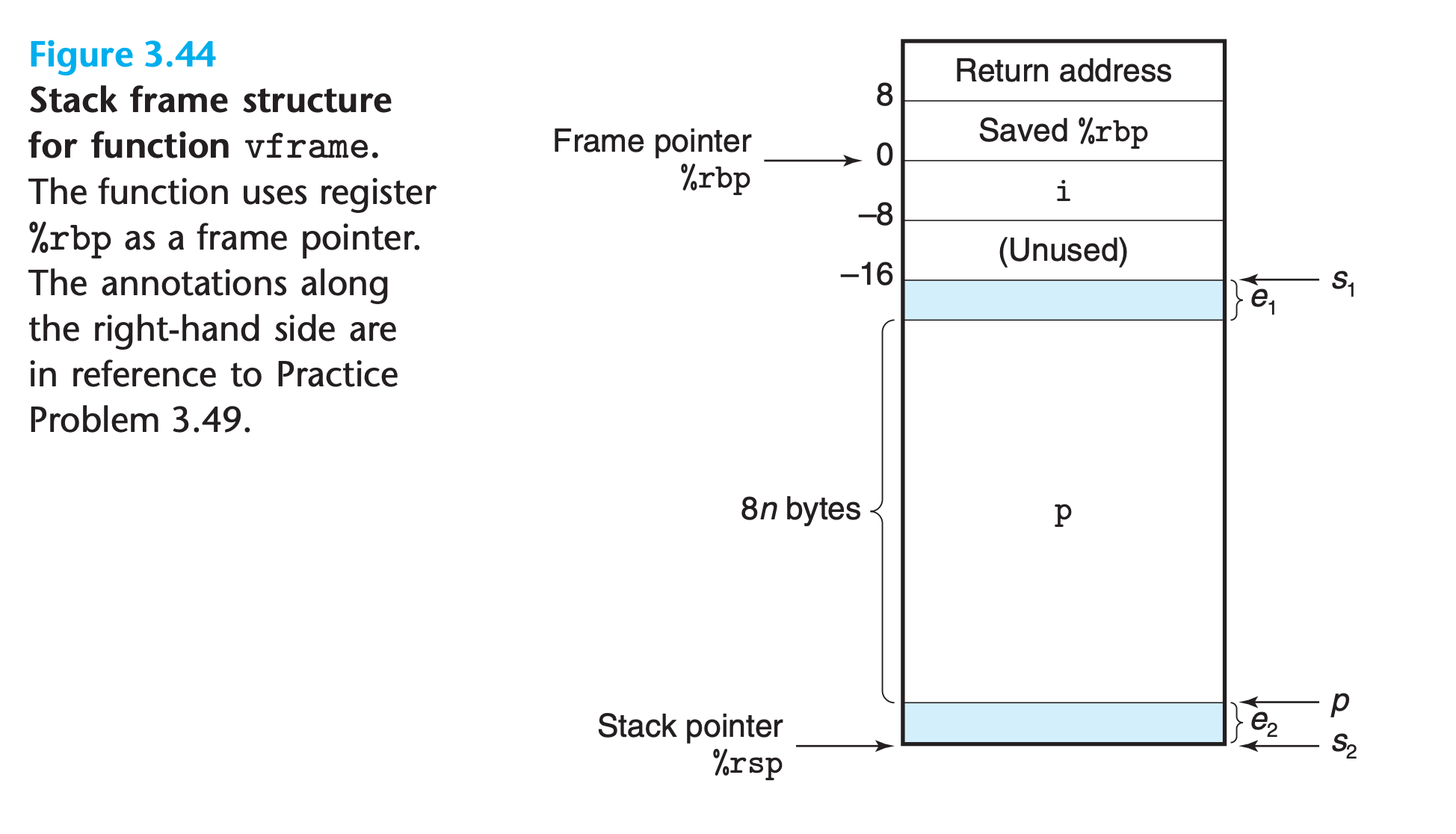
frame pointer

  • it references fixed-length local variables, such as i, at offsets relative to %rbp

  • At the end of the function, the frame pointer is restored to its previous value using the leave instruction.

    This instruction takes no arguments. It is equivalent to executing the following two instructions:

    1
    2
    3
    movq %rbp, %rsp 	#Set stack pointer to beginning of frame
    popq %rbp 			#Restore saved %rbp and set stack ptr
    					#to end of caller’s frame

  • In earlier versions of x86 code, the frame pointer was used with every function call. With x86-64 code, it is used only in cases where the stack frame may be of variable size

Practice Problem 3.49

In this problem, we will explore the logic behind the code where space is allocated for variable-size array p.

let us let $s_1$ denote the address of the stack pointer after executing the subq instruction at line 4.This instruction allocates the space for local variable i.

Let $s_2$ denote the value of the stack pointer after executing the subq instruction of line 7.This instruction allocates the storage for local array p.

Finally, let $p$ denote the value assigned to registers %r8 and %rcx in the instructions of lines 10–11. Both of these registers are used to reference array p

Figure 3.44 diagrams the positions of the locations indicated by $s_1$,$ s_2$, and $p$. It also shows that there may be an offset of $e_2$ bytes between the values of $s_1$ and $p$. This space will not be used. There may also be an offset of $e_1$ bytes between the end of array p and the position indicated by $s_1$​

A. Explain, in mathematical terms, the logic in the computation of $s_2$​ on lines 5–7. Hint: Think about the bit-level representation of −16 and its effect in the andq instruction of line 6.

B. Explain, in mathematical terms, the logic in the computation of p on lines 8–10. Hint: You may want to refer to the discussion on division by powers of 2 in Section 2.3.7.

C. For the following values of n and s1, trace the execution of the code to determine what the resulting values would be for s2, p, e1, and e2.

n s1 s2 p e1 e2
5 2065
6 2064

D. What alignment properties does this code guarantee for the values of s2 and p?

My solution : :warning:

A:

1
2
3
leaq	22(,%rdi,8), %rax	# rax = 8*n + 22
andq	$-16, %rax			# rax = (8*n + 22) & -16
subq	%rax, %rsp			# rsp -= (8*n + 22) & -16
1
2
3
4
& -16 means ((8*n+22) >> 4) << 4  , == ((8*n+22) / 16 * 16)
when n = 2k - 1 is odd, the result is  8(n+1)
when n = 2k is even, the result is 8n+16
align the space to 16

B:

1
2
3
4
5
6
7
8
9
10
	leaq	7(%rsp), %rax		# rax = rsp + 7
	shrq	$3, %rax			# rax = (rsp+7) / 8
	leaq	0(,%rax,8), %r8		# r8 = ((rsp+7) / 8) * 8
# division for negative value
# add bias (2^3-1) = 7
# divide 2^3 : (rax >> 3)
# r8 = rax // 8 , round towards 0
# division for positive value
# round towards +infinty
# finally multiple by 8

C:

n s1 s2 p e1 e2
5 2065 2017 2024 1 7
6 2064 2000 2000 16 0

$$
n = 5 , s_1 = 2065
$$

$$
s_2 = s_1 -(8\times 5 + 8)=2065 -48 = 2017
$$

$$
e_2 = p - s_2 = 7
$$

$$
e_ 1= s_1 - (s_2 + (8\times n)) = 1
$$

D:

Align to 8 for p, no alignment for s2

Solution on the book :

A. The leaq instruction of line 5 computes the value $8n + 22$, which is then rounded down to the nearest multiple of 16 by the andq instruction of line 6. The resulting value will be $8n + 8$ when n is odd and $8n + 16$ when n is even, and this value is subtracted from s1 to give s2.

B. The three instructions in this sequence round s2 up to the nearest multiple of 8. They make use of the combination of biasing and shifting that we saw for dividing by a power of 2 in Section 2.3.7.

D. We can see that s2 is computed in a way that preserves whatever offset s1 has with the nearest multiple of 16. We can also see that p will be aligned on a multiple of 8, as is recommended for an array of 8-byte elements.

Tips

1
2
3
4
5
#define N 5
int twodimensions [N][N];
//type(twodimensions) is not int** !!
typedef int arr [N];
arr * p = twodimensions; //this is correct, *(++p) == twodimensions[1]

stick to pointer arithmetic principle when you interact with array.

1
2
3
4
5
6
7
8
arr a1 = { 1 , 2 , 3, 4, 5};
arr a2 = { 1 , 2 , 3, 4, 5};
arr a3 = { 1 , 2 , 3, 4, 5};
arr * pointers [3] = { a1 , a2 , a3 }; // wrong , a1 is converted to arr* from int*
int * ps  [3]= { a1 , a2 , a3 };
printf("%p\n" , pointers[0]+1); 
printf("%p\n" , ps[0]+1); 
printf("%p\n" , a1+1);

3.11 Floating-Point Code

The floating-point architecture for a processor consists of the different aspects that affect how programs operating on floating-point data are mapped onto the machine, including

  • How floating-point values are stored and accessed
  • The instructions that operate on floating-point data.
  • The conventions used for passing floating-point values as arguments to functions and for returning them as results.
  • The conventions for how registers are preserved during function calls
Historical view
  • in 1997, both Intel and AMD have incorporated successive generations of media instructions to support graphics and image processing.
    • These instructions originally focused on SIMD(Simple Instruction Multiple Data), allowing the same operation is performed on a number of different data values in parallel
  • Over the years, there has been a progression of these extensions
    • The name has changed from MMX to SSE(Stream SIMD Extension), and most recently, AVX(Advanced Vector Extension)
    • Each of these extensions manages data in sets of registers
    • They have different register names and register sizes
  • All processors capable of executing x86-64 code support SSE2 or higher, and hence x86-64 floating point is based on SSE or AVX, including conventions for passing procedure arguments and return values
    • Our presentation is based on AVX2
    • Gcc will generate AVX2 code when given the command-line parameter -mavx2

registers

  • the AVX floating-point architecture allows data to be stored in 16 YMM registers, named %ymm0–%ymm15.

  • Each YMM register is 256 bits (32 bytes) long.

  • When operating on scalar data, these registers only hold floating-point data, and only the low-order 32 bits (for float) or 64 bits (for double) are used.

    (Set unused space to 0 in register but only change 32 or 64 bits in memory !)

3.11.1 Floating-Point Movement and Conversion Operations

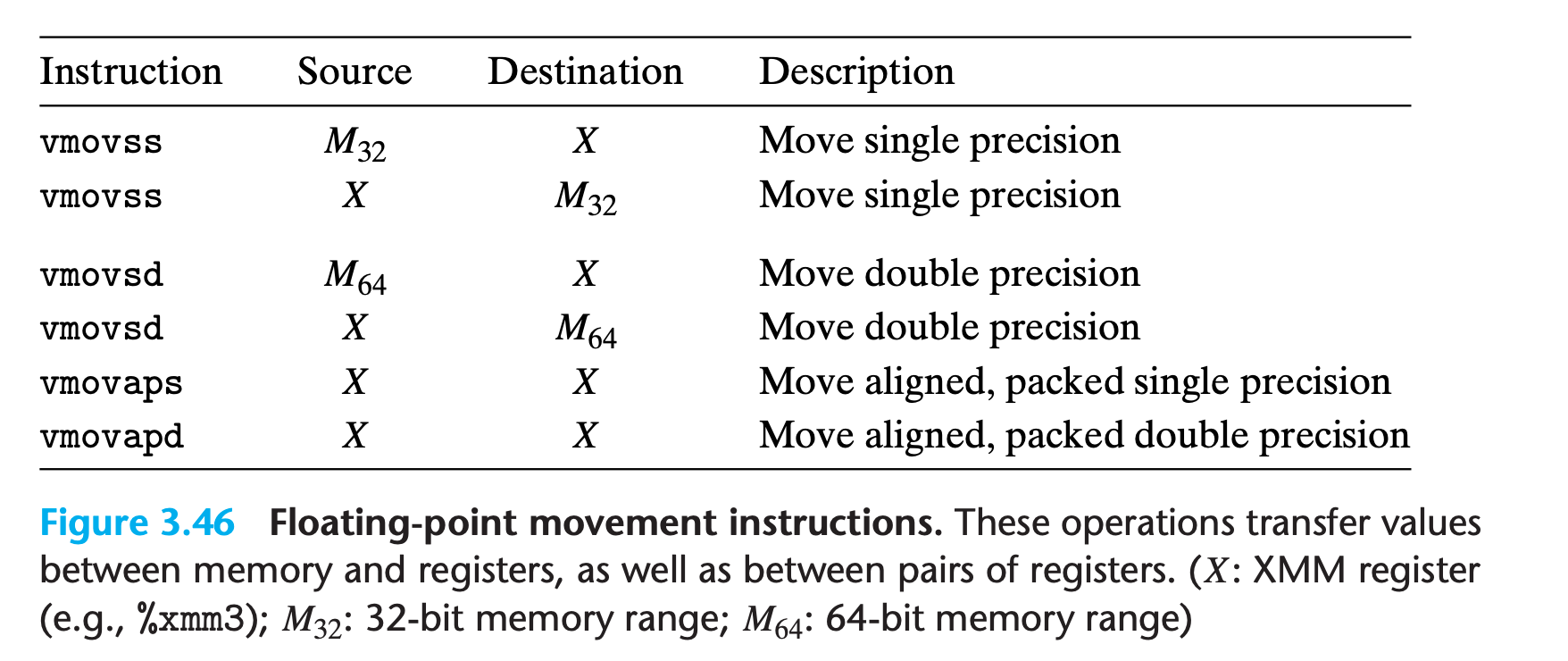
mov instructions

  • Memory references are specified in the same way as for the integer mov instructions, with all of the different possible combinations of displacement, base register, index register, and scaling factor

  • Gcc uses the scalar movement operations only to transfer data from memory to an XMM register or from an XMM register to memory.

    For transferring data between two XMM registers, it uses one of two different instructions for copying the entire contents of one XMM register to another

    vmovaps for single precision, vmovapd for double precision

  • For example

    1
    2
    3
    4
    5
    float float_mov(float v1, float *src, float *dst) {
    float v2 = *src;
    *dst = v1;
    return v2;
    }
    1
    $ gcc float.c -Og -mavx2 -S -o  float.s && ./wash float.s && cat clean_float.s
    1
    2
    3
    4
    5
    6
    # v1 in %xmm0, src in %rdi, dst in %rsi
    float_mov:
    	vmovss	(%rdi), %xmm1
    	vmovss	%xmm0, (%rsi)
    	vmovaps	%xmm1, %xmm0
    	ret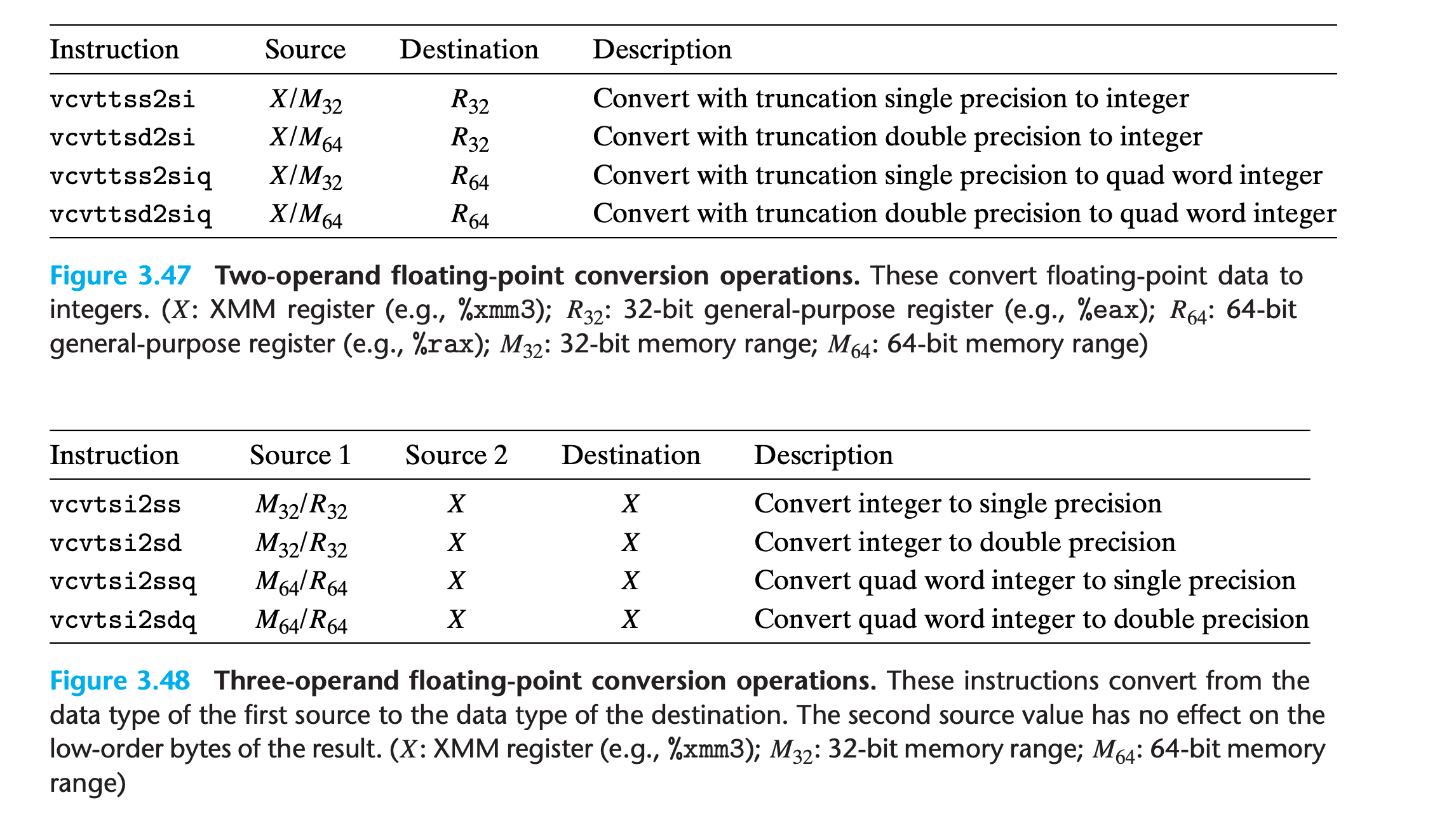

    conversion instructions

When converting floating-point values to integers, they perform truncation, rounding values toward zero

For example

  • float to int : vcvttss2si %xmm0, %rdx
  • float to double : vcvtss2sd %xmm0,%xmm0,%xmm0

(There are situations where gcc generate weird code for conversion, if this happens, STFW or check page 334)

1
2
3
#Conversion from single to double precision
vunpcklps %xmm0, %xmm0, %xmm0 	#Replicate first vector element
vcvtps2pd %xmm0, %xmm0 			#Convert two vector elements to double

Practice Problem 3.50

For the following C code, the expressions val1 toval4 all map to the program values i, f, d, and l:

1
2
3
4
5
6
7
8
double fcvt2(int *ip, float *fp, double *dp, long l)
{
int i = *ip; float f = *fp; double d = *dp;
*ip = (int) val1;
*fp = (float) val2;
*dp = (double) val3;
return (double) val4;
}

Determine the mapping, based on the following x86-64 code for the function:

1
2
3
4
5
6
7
8
9
10
11
12
fcvt2:
    movl (%rdi), %eax
    vmovss (%rsi), %xmm0
    vcvttsd2si (%rdx), %r8d
    movl %r8d, (%rdi)
    vcvtsi2ss %eax, %xmm1, %xmm1
    vmovss %xmm1, (%rsi)
    vcvtsi2sdq %rcx, %xmm1, %xmm1
    vmovsd %xmm1, (%rdx)
    vunpcklps %xmm0, %xmm0, %xmm0
    vcvtps2pd %xmm0, %xmm0
    ret

My solution : :white_check_mark:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# double fcvt2(int *ip, float *fp, double *dp, long l)
fcvt2:        
    movl (%rdi), %eax       # eax = *ip
    vmovss (%rsi), %xmm0    # xmm0 = *fp 
    vcvttsd2si (%rdx), %r8d # r8d = (int)*dp
    movl %r8d, (%rdi)       # *ip = (int)*dp 
    vcvtsi2ss %eax, %xmm1, %xmm1   # xmm1 = (float)*ip 
    vmovss %xmm1, (%rsi)           # *fp = (float)*ip
    vcvtsi2sdq %rcx, %xmm1, %xmm1  # xmm1 = (double)l  
    vmovsd %xmm1, (%rdx)           # *dp = (double)l
    vunpcklps %xmm0, %xmm0, %xmm0  # ret = xmm0 = (double)*fp
    vcvtps2pd %xmm0, %xmm0         
    ret        
# val1 = *dp
# val2 = *ip
# val3 = l
# val4 = *fp

Practice Problem 3.51

The following C function converts an argument of type src_t to a return value of type dst_t, where these two types are defined using typedef:

1
2
3
4
5
dest_t cvt(src_t x)
{
dest_t y = (dest_t) x;
return y;
}

For execution on x86-64, assume that argument x is either in %xmm0 or in the appropriately named portion of register %rdi. One or two instructions are to be used to perform the type conversion and to copy the value to the appropriately named portion of register %rax or %xmm0 . Show the instruction(s), including the source and destination registers.

1
2
3
4
5
6
Tx 		Ty 		Instruction(s)
long 	double 	vcvtsi2sdq %rdi, %xmm0
double 	int
double 	float
long 	float
float 	long

My solution : :white_check_mark:

1
2
3
4
5
6
Tx 		Ty 		Instruction(s)
long 	double 	vcvtsi2sdq %rdi,%xmm0, %xmm0
double 	int		vcvttsd2si  %xmm0,%eax
double 	float	vcvtsd2ss  (%rdi), %xmm0, %xmm0
long 	float	vcvtsi2ssq %rdi,%xmm0, %xmm0
float 	long	vcvttss2siq %xmm0,%rax

3.11.2 Floating-Point Code in Procedures

the following conventions are observed:

  • Up to eight floating-point arguments can be passed in XMM registers %xmm0 to %xmm7. These registers are used in the order the arguments are listed. Additional floating-point arguments can be passed on the stack.
  • A function that returns a floating-point value does so in register %xmm0.
  • All XMM registers are caller saved. The callee may overwrite any of these registers without first saving it.

Practice Problem 3.52

For each of the following function declarations, determine the register assignments for the arguments:

1
2
3
4
A. double g1(double a, long b, float c, int d);
B. double g2(int a, double *b, float *c, long d);
C. double g3(double *a, double b, int c, float d);
D. double g4(float a, int *b, float c, double d);

My solution : :white_check_mark:

1
2
3
4
5
6
7
8
A. double g1(double a, long b, float c, int d);
//a in %xmm0, b in %rdi , c in %xmm1 , d in %esi
B. double g2(int a, double *b, float *c, long d);
// a in %edi , b in %rsi , c in %rdx , d in %rcx
C. double g3(double *a, double b, int c, float d);
// a in %rdi , b in %xmm0 , c in %esi , d in %xmm1
D. double g4(float a, int *b, float c, double d);
// a in %xmm0 , b in %rdi , c in %xmm1 , d in %xmm2

3.11.3 Floating-Point Arithmetic Operations

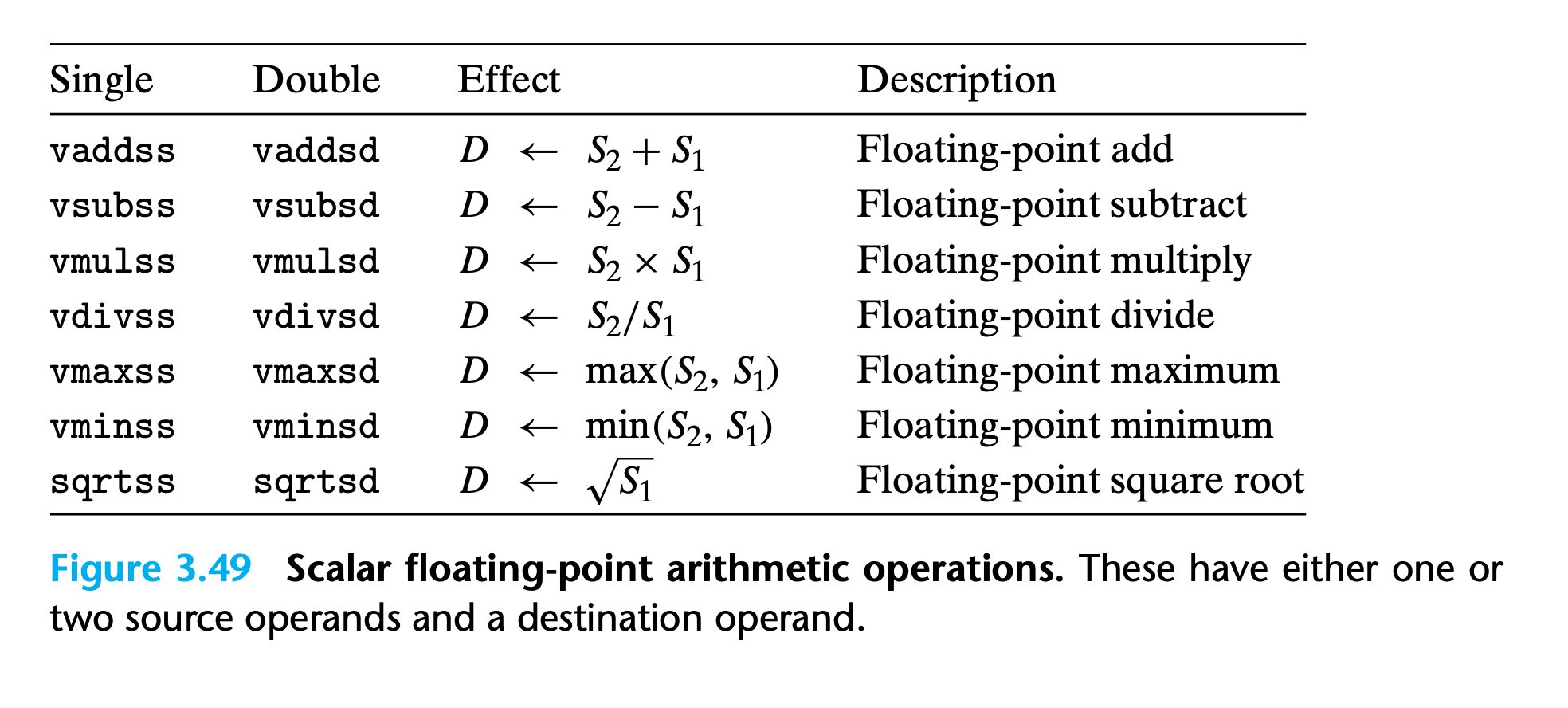
float point arithmetic instructions

  • Each has either one (S1) or two (S1, S2) source operands and a destination operand D.
  • The first source operand S1 can be either an XMM register or a memory location. The second source operand must be a XMM register
  • Each operation has an instruction for single precision and an instruction for double precision.

For example

1
2
3
4
double funct(double a, float x, double b, int i)
{
return a*x - b/i;
}
1
2
3
4
5
6
7
8
funct:
	vcvtss2sd	%xmm1, %xmm1, %xmm1	# x = (double)x
	vmulsd	%xmm0, %xmm1, %xmm0		# a = a*x
	vxorpd	%xmm1, %xmm1, %xmm1		# x = 0
	vcvtsi2sd	%edi, %xmm1, %xmm1	# x = (double)i
	vdivsd	%xmm1, %xmm2, %xmm2		# b = b/x
	vsubsd	%xmm2, %xmm0, %xmm0		# return a-b
	ret

Practice Problem 3.53

For the following C function, the types of the four arguments are defined by typedef:

1
2
3
4
double funct1(arg1_t p, arg2_t q, arg3_t r, arg4_t s)
{
return p/(q+r) - s;
}

When compiled, gcc generates the following code:

1
2
3
4
5
6
7
8
9
10
#double funct1(arg1_t p, arg2_t q, arg3_t r, arg4_t s)
funct1:
 vcvtsi2ssq %rsi, %xmm2, %xmm2
 vaddss %xmm0, %xmm2, %xmm0
 vcvtsi2ss %edi, %xmm2, %xmm2
 vdivss %xmm0, %xmm2, %xmm0
 vunpcklps %xmm0, %xmm0, %xmm0
 vcvtps2pd %xmm0, %xmm0
 vsubsd %xmm1, %xmm0, %xmm0
 ret

Determine the possible combinations of types of the four arguments (there may be more than one).

My solution : :white_check_mark:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#double funct1(arg1_t p, arg2_t q, arg3_t r, arg4_t s)
funct1:
 vcvtsi2ssq %rsi, %xmm2, %xmm2	# xmm2 = (float)rsi  q or r in %rsi, long
 vaddss %xmm0, %xmm2, %xmm0		# xmm0 = q+r	q or r in %xmm0, float
 vcvtsi2ss %edi, %xmm2, %xmm2	# xmm2 = (float)edi
 vdivss %xmm0, %xmm2, %xmm0		# xmm0 = xmm2/xmm0 = p/xmm0
 vunpcklps %xmm0, %xmm0, %xmm0	# xmm0 = (double)xmm0
 vcvtps2pd %xmm0, %xmm0
 vsubsd %xmm1, %xmm0, %xmm0		# xmm0 = xmm0 - xmm1 , s in xmm1
 ret
# arg1_t is int
# arg4_t is double
# arg2_t is long or float
# arg3_t is float or long

Practice Problem 3.54

Function funct2 has the following prototype:

1
double funct2(double w, int x, float y, long z);

Gcc generates the following code for the function:

1
2
3
4
5
6
7
8
9
10
11
#double funct2(double w, int x, float y, long z)
#w in %xmm0, x in %edi, y in %xmm1, z in %rsi
funct2:
 vcvtsi2ss %edi, %xmm2, %xmm2
 vmulss %xmm1, %xmm2, %xmm1
 vunpcklps %xmm1, %xmm1, %xmm1
 vcvtps2pd %xmm1, %xmm2
 vcvtsi2sdq %rsi, %xmm1, %xmm1
 vdivsd %xmm1, %xmm0, %xmm0
 vsubsd %xmm0, %xmm2, %xmm0
 ret

Write a C version of funct2.

My solution :

1
2
3
4
5
6
7
8
9
10
11
#double funct2(double w, int x, float y, long z)
#w in %xmm0, x in %edi, y in %xmm1, z in %rsi
funct2:
 vcvtsi2ss %edi, %xmm2, %xmm2	# xmm2 = (float)x
 vmulss %xmm1, %xmm2, %xmm1		# xmm1 = xmm1 * xmm2	y = y*x
 vunpcklps %xmm1, %xmm1, %xmm1	# xmm2 = (double)y
 vcvtps2pd %xmm1, %xmm2
 vcvtsi2sdq %rsi, %xmm1, %xmm1	# xmm1 = (double)z
 vdivsd %xmm1, %xmm0, %xmm0		# xmm0 = xmm0 / xmm1 	w = w/z
 vsubsd %xmm0, %xmm2, %xmm0		# res = xmm2 - xmm0		return y-w/z
 ret
1
2
3
double funct2(double w, int x, float y, long z){
    return y*x-w/z;
}

3.11.4 Defining and Using Floating-Point Constants

Unlike integer arithmetic operations, AVX floating-point operations cannot have immediate values as operands. Instead, the compiler must allocate and initialize storage for any constant values .The code then reads the values from memory. .

For example

1
2
3
4
double cel2fahr(double temp)
{
return 1.8 * temp + 32.0;
}
1
2
3
4
5
6
7
8
9
10
11
cel2fahr:
	vmulsd	.LC0(%rip), %xmm0, %xmm0
	vaddsd	.LC1(%rip), %xmm0, %xmm0
	ret
.LC0:
	.long	3435973837
	.long	1073532108
	.align 8
.LC1:
	.long	0
	.long	1077936128

Little endian mechine:

1
2
3
4
5
6
7
8
from struct import unpack
highorder = hex(1073532108)[2:]
loworder = hex(3435973837)[2:]
hexs = highorder + loworder
buf = int(hexs , 16).to_bytes(8,'little',signed=True)
tp = unpack('d' , buf)
print(tp[0])
# 1.8

Practice Problem 3.55

Show how the numbers declared at label .LC1 encode the number 32.0.

1
2
3
highorder = hex(1077936128)[2:]
loworder = hex(0)[2:] * 8
# 32.0

3.11.5 Using Bitwise Operations in Floating-Point Code

bitwise instructions

These operations all act on packed data, meaning that they update the entire destination XMM register, applying the bitwise operation to all the data in the two source registers.

Practice Problem 3.56

Consider the following C function, where EXPR is a macro defined with #define:

1
2
3
double simplefun(double x) {
return EXPR(x);
}

Below, we show the AVX2 code generated for different definitions of EXPR, where value x is held in %xmm0. All of them correspond to some useful operation on floating-point values. Identify what the operations are. Your answers will require you to understand the bit patterns of the constant words being retrieved from memory.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# A
	vmovsd .LC1(%rip), %xmm1        
    vandpd %xmm1, %xmm0, %xmm0    
.LC1:                   
    .long 4294967295    
    .long 2147483647    
    .long 0             
    .long 0
# B
	vxorpd %xmm0, %xmm0, %xmm0
# C
    vmovsd .LC2(%rip), %xmm1        
    vxorpd %xmm1, %xmm0, %xmm0
.LC2:    
    .long 0
    .long -2147483648
    .long 0
    .long 0

My solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# A
	vmovsd .LC1(%rip), %xmm1  		# xmm1 =  011111111...111     
    vandpd %xmm1, %xmm0, %xmm0    	# xmm0 = xmm0 & xmm1
.LC1:                   
    .long 4294967295    
    .long 2147483647    
    .long 0             
    .long 0
# B
	vxorpd %xmm0, %xmm0, %xmm0	# xmm0 = xmm0 ^ xmm0 = 0
# C
    vmovsd .LC2(%rip), %xmm1   	# xmm1 = 10000..000
    vxorpd %xmm1, %xmm0, %xmm0	# xmm0 = xmm1 ^ xmm0
.LC2:    
    .long 0
    .long -2147483648
    .long 0
    .long 0

Solution on the book

1
2
3
4
5
6
//A
#define EXPR(x) fabs(x)
//B
#define EXPR(x) 0.0
//C
#define EXPR(x) -x

3.11.6 Floating-Point Comparison Operations

cmp instructions

(Instructions are vucomiss and vucomisd)

The floating-point comparison instructions set three condition codes: the zero flag ZF, the carry flag CF, and the parity flag PF.

  • The parity flag PF:
    • For integer arithmetic and logical operation, if the least significant byte has even parity (i.e., an even number of ones in the byte) the flag will be 1.
    • For floating-point comparisons, the flag is set when either operand is NaN
    • when operate with float point number, if PF is set, the comparison will fail.

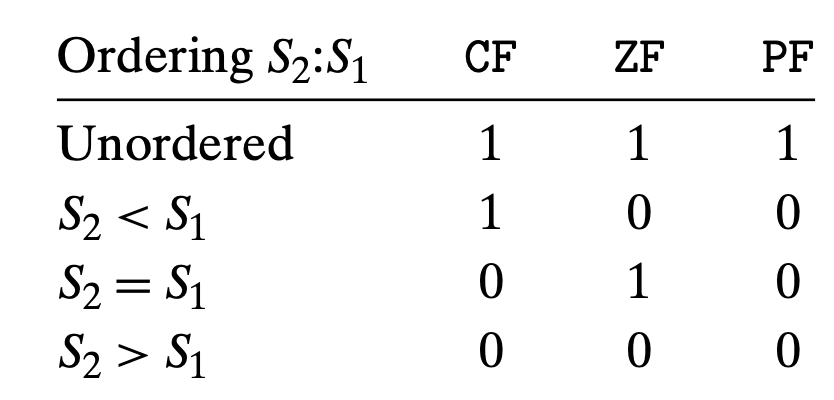
comparison conditions

  • The unordered case occurs when either operand is NaN.
    • Commonly, the jp (for “jump on parity”) instruction is used to conditionally jump when a floating-point comparison yields an unordered result.
  • Other situations are like unsigned comparison
    • ZF is set when the two operands are equal
    • CF is set when S2 < S1
    • Instructions such as ja and jb are used to conditionally jump on various combinations of these flags.

Practice Problem 3.57

Function funct3 has the following prototype:

1
double funct3(int *ap, double b, long c, float *dp);

For this function, gcc generates the following code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
funct3:
	vmovss	(%rdx), %xmm1
	vxorpd	%xmm2, %xmm2, %xmm2
	vcvtsi2sd	(%rdi), %xmm2, %xmm2
	vucomisd	%xmm2, %xmm0
	ja	.L7
	vaddss	%xmm1, %xmm1, %xmm1
	vxorps	%xmm0, %xmm0, %xmm0
	vcvtsi2ssq	%rsi, %xmm0, %xmm0
	vaddss	%xmm1, %xmm0, %xmm0
	vcvtss2sd	%xmm0, %xmm0, %xmm0
	ret
.L7:
	vxorps	%xmm0, %xmm0, %xmm0
	vcvtsi2ssq	%rsi, %xmm0, %xmm0
	vmulss	%xmm1, %xmm0, %xmm0
	vcvtss2sd	%xmm0, %xmm0, %xmm0
	ret

Write a C version of funct3.

My solution: :white_check_mark:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# double funct3(int *ap, double b, long c, float *dp);
funct3:
	vmovss	(%rdx), %xmm1			# xmm1 = *dp		
	vxorpd	%xmm2, %xmm2, %xmm2		# xmm2 = 0.0
	vcvtsi2sd	(%rdi), %xmm2, %xmm2# xmm2 = (double)*ap
	vucomisd	%xmm2, %xmm0		# if (xmm0 > xmm2) goto L7;
	ja	.L7
	vaddss	%xmm1, %xmm1, %xmm1		# xmm1 = xmm1 + xmm1
	vxorps	%xmm0, %xmm0, %xmm0		# xmm0 = 0.0
	vcvtsi2ssq	%rsi, %xmm0, %xmm0	# xmm0 = (float)c
	vaddss	%xmm1, %xmm0, %xmm0		# xmm0 = xmm0 + xmm1
	vcvtss2sd	%xmm0, %xmm0, %xmm0	# xmm0 = (double)xmm0
	ret
.L7:
	vxorps	%xmm0, %xmm0, %xmm0		# xmm0 = 0.0
	vcvtsi2ssq	%rsi, %xmm0, %xmm0	# xmm0 = (float)c
	vmulss	%xmm1, %xmm0, %xmm0		# xmm0 = xmm0 * xmm1
	vcvtss2sd	%xmm0, %xmm0, %xmm0	# xmm0 = (double)xmm0
	ret
1
2
3
4
5
6
7
8
9
10
double funct3(int *ap, double b, long c, float *dp){
    float d = *dp;
    double a = (double)*ap;
    if(b > a){
        return (double)(c*d);
    }
    else{
       	return (double)(c+2*d);
    }
}

3.11.7 Observations about Floating-Point Code

  • AVX2 code involves many more different instructions and formats than is usually seen with functions that perform only integer arithmetic.

  • AVX2 also has the potential to make computations run faster by performing parallel operations on packed data.

    See Web Aside opt:simd on page 582 to see how this can be done.

Tips

  • compiling C++ is very similar to compiling C.

    In fact, early implementations of C++ first performed a source-to-source conversion from C++ to C and generated object code by running a C compiler on the result

  • Java is implemented in an entirely different fashion.

    The object code of Java is a special binary representation known as Java byte code.

  • check stack memory limit :

    • csh or zsh : limit
    • bash : ulimit -a
    • use alloca function to allocate space on stack, but if no available space remains, the behavior will be undefined

  • dangerous functions :

    1
    2
    3
    4
    5
    gets()	//use fgets, please
    fscanf(),sscanf(),scanf() with %s
    strcpy()
    strcat()
    ...

  • attack strategies

    • Brute force to overcome ASLR
    • ROP to overcome non-executeable stack
    • However, canary is quite hard to overcome

  • When you do ROP, focus on the byte sequence and don’t be limited by instructions

    For example

    1
    2
    3
    4
    movl $0xc78948d4,(%rdi)		c7 07 d4 48 89 c7
    ret							c3

    movq %rax,$rdi	48 89 c7