csapp

Ch5

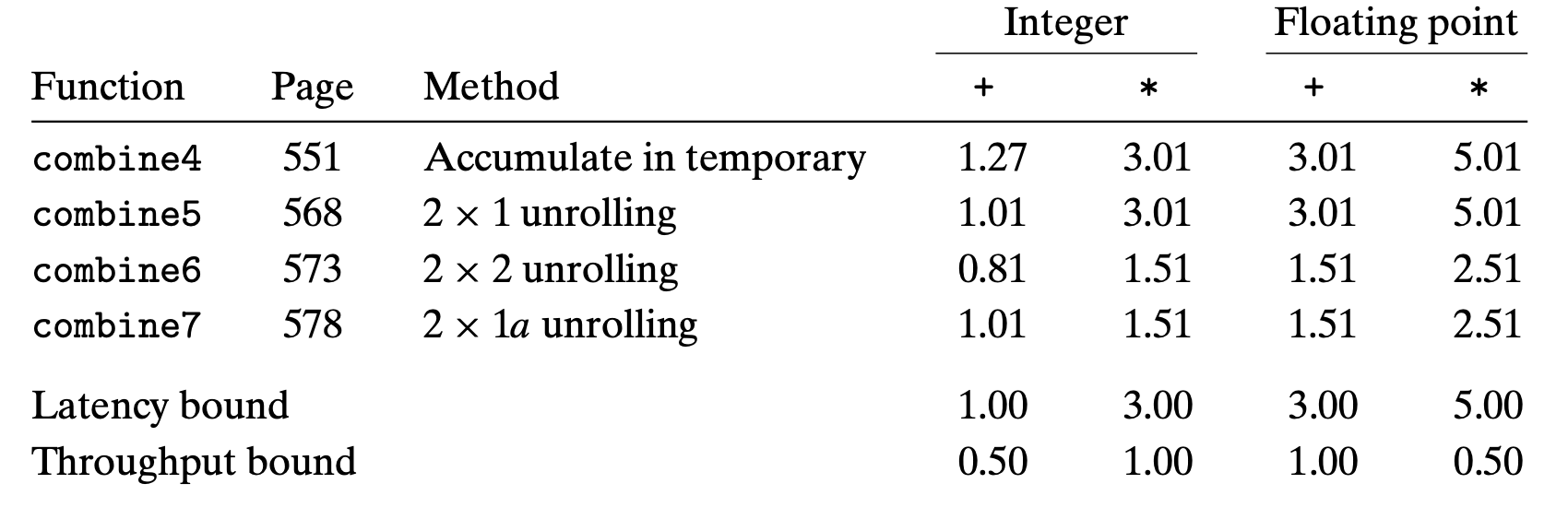
Optimizing Program Performance

Writing an efficient program requires several types of activities

  • select an appropriate set of algorithms and data structures

  • write source code that the compiler can effectively optimize to turn into efficient executable code

  • divide a task into portions that can be computed in parallel, on some combination of multiple cores and multiple processors

    ( Even when exploiting parallelism, it is important that each parallel thread execute with maximum performance)

In general, programmers must make a trade-off between how easy a program is to implement and maintain, and how fast it runs

(For example simple bubble sort vs quick sort)

(For example optimizations will reduce readability)

When optimizing the program, the programmer work together with the compiler

  • Programmers should eliminate unnecessary work, making the code perform its intended task as efficiently as possible.(Reduce function call, memory reference ….)

  • To maximize the performance, a model of the target machine is very important.

    How instructions are executed on the target machine is vital

    (For example, the compiler need these information to decide it should choose to generate a mulitplication instruction or a combination of addition and shifting)

    (On some machines, we can even perform an instruction-level parallelism, executing multiple instructions simultaneously)

Optimization can be a difficult job
  • Performance can depend on many detailed features of the processor design for which we have relatively little documentation or understanding
  • It can be difficult to explain exactly why a particular code sequence has a particular execution time.
  • So optimization is not a linear job of transfering code by applying several rules (as we will do), but it is a lot of trial-and-error experimentation is required.

It might seem strange to keep modifying the source code in an attempt to coax the compiler into generating efficient code, but this is indeed how many high-performance programs are written.

5.1 Capabilities and Limitations of Optimizing Compilers

Compilers must be careful to apply only safe optimizations to a program

For example

1
2
3
4
5
6
7
8
9
10
void twiddle1(long *xp, long *yp)
{
 *xp += *yp;
 *xp += *yp;
}

 void twiddle2(long *xp, long *yp)
{
 *xp += 2* *yp;
}
  • These two functions are seemingly same
  • twiddle2 will be more efficient than twiddle1 since it only refers the memory for 3 times rather than 4 times
  • However, if xp == yp, twiddle1 will gives 4 * (*xp) while twiddle2 gives 3 * *(*xp)
  • So the complier don’t know how the function will be called, so it cannot generate optimized code based on twiddle2 for twiddle1

The case where two pointers may designate the same memory location is known as ==memory aliasing==, which is a major optimization blockers, preventing compiler from applying some optimization

Another example

1
2
3
4
5
6
x = 1000; y = 3000;
*q = y; /* 3000 */
*p = x; /* 1000 */
t1 = *q; /* 1000 or 3000 */
//if p != q , t1 == 3000
//if p == q, t1 == 1000

Practice Problem 5.1

The following problem illustrates the way memory aliasing can cause unexpected program behavior. Consider the following procedure to swap two values:

1
2
3
4
5
6
void swap(long *xp, long *yp)
{
*xp = *xp + *yp; /* x+y */
*yp = *xp - *yp; /* x+y-y = x */
*xp = *xp - *yp; /* x+y-x = y */
}

If this procedure is called with xp equal to yp, what effect will it have?

My solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <stdio.h>
void swap(long *xp, long *yp);
void sp(long * xp , long * yp);
int main(){
    long a = 123;
    long b = 456;
    printf("%ld %ld\n" , a , b);
    swap(&a, &b);
    printf("%ld %ld\n" , a , b);
    sp(&a, &b);
    printf("%ld %ld\n" , a , b);
    swap(&a, &a);
    sp(&b, &b);
    printf("%ld %ld\n" , a , b); 
}
/* Swap value x at xp with value y at yp */
void swap(long *xp, long *yp)
{
*xp = *xp + *yp; /* x+y */
*yp = *xp - *yp; /* x+y-y = x */
*xp = *xp - *yp; /* x+y-x = y */
}
void sp(long * xp , long * yp){
    *xp = *xp ^ *yp;
    *yp = *xp ^ *yp; // x ^ y ^ y = x 
    *xp = *xp ^ *yp; // x ^ y ^ x = y
}

A second optimization blocker is due to ==function calls==.

1
2
3
4
5
6
7
long f();
long func1() {
return f() + f() + f() + f();
}
long func2() {
return 4*f();
}

  • func1 call f 4 times while func2 call f only once

  • Again the compiler cannot optimize func1 into func2

  • An hazard example

    1
    2
    3
    4
    long globaldata = 0;
    f(){ return globaldata++ ;}
    //func1()  = 0 + 1 + 2 + 3 == 6
    //func2() = 0 * 4 == 0

  • Code involving function calls can be optimized by a process known as inline substitution, where the function call is replaced by the code for the body of the function(some compiler will do this, but gcc won’t)

5.2 Expressing Program Performance

We introduce the metric cycles per element, abbreviated CPE, to express program performance in a way that can guide us in improving the code

For example, here are some codes for computation the prefix-sum of a float vector

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/* Compute prefix sum of vector a */
void psum1(float a[], float p[], long n)
{
    long i;
    p[0] = a[0];
    for (i = 1; i < n; i++)
    p[i] = p[i-1] + a[i];
}

//using loop unrolling technique to reduce times of iteration
void psum2(float a[], float p[], long n)
{
    long i;
    p[0] = a[0];
    for (i = 1; i < n-1; i+=2) {
        float mid_val = p[i-1] + a[i];
        p[i] = mid_val;
        p[i+1] = mid_val + a[i+1];
}
/* For even n, finish remaining element */
if (i < n) p[i] = p[i-1] + a[i];
}

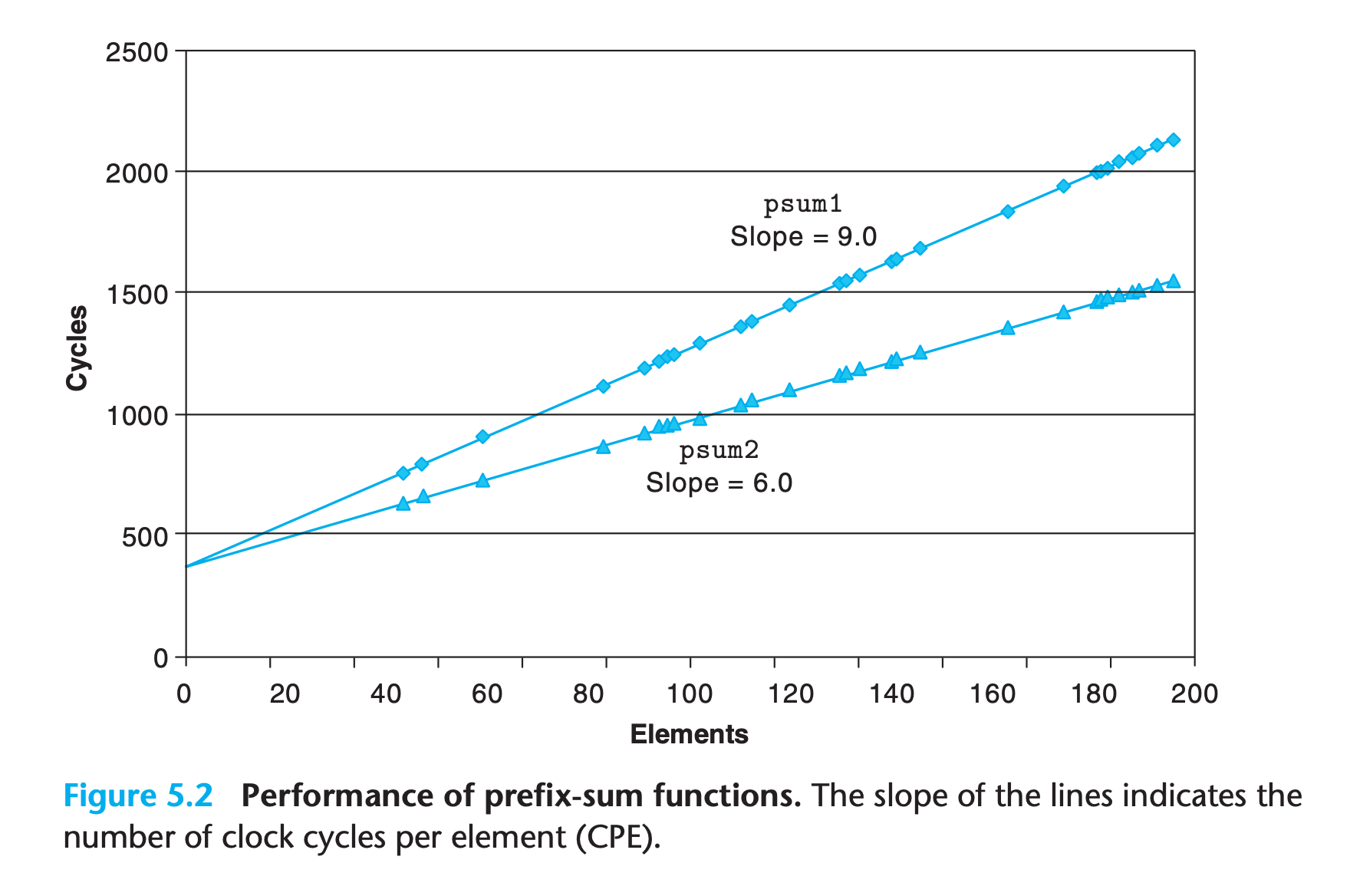
performance

The performance can be fit into a linear module of y = kx + b

  • b is the time used to initialized the loop
  • k is what we called CPE(how many clocks are needed to operate on one element)

Practice Problem 5.2

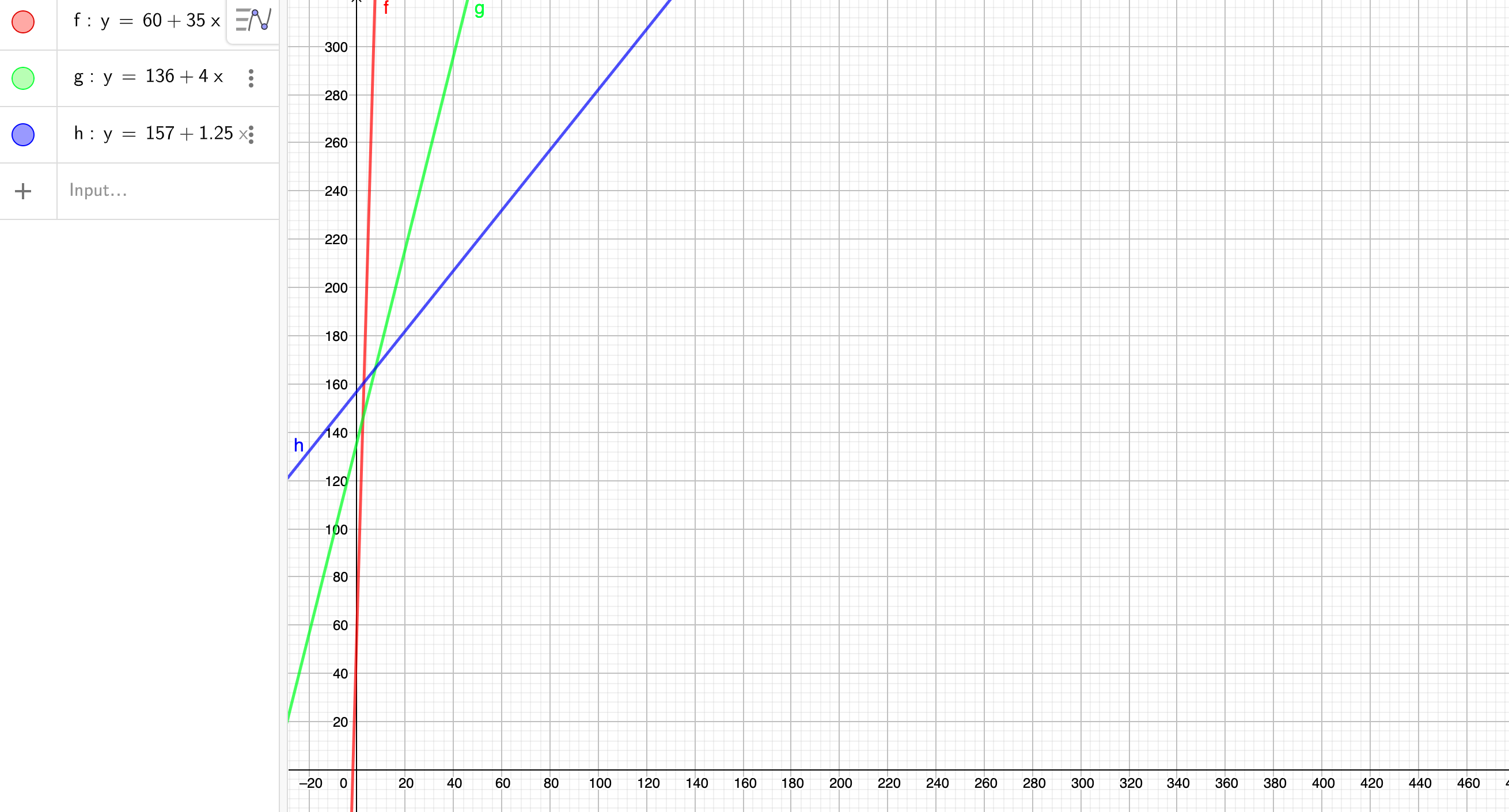
Later in this chapter we will start with a single function and generate many different variants that preserve the function’s behavior, but with different performance characteristics. For three of these variants, we found that the run times (in clock cycles) can be approximated by the following functions:

1
2
3
Version 1: 60 + 35n
Version 2: 136 + 4n
Version 3: 157 + 1.25n

For what values of n would each version be the fastest of the three? Remember that n will always be an integer

My solution : :white_check_mark:

(Graph drawn by geogebra)

graph

Let’s zoom in and do some math

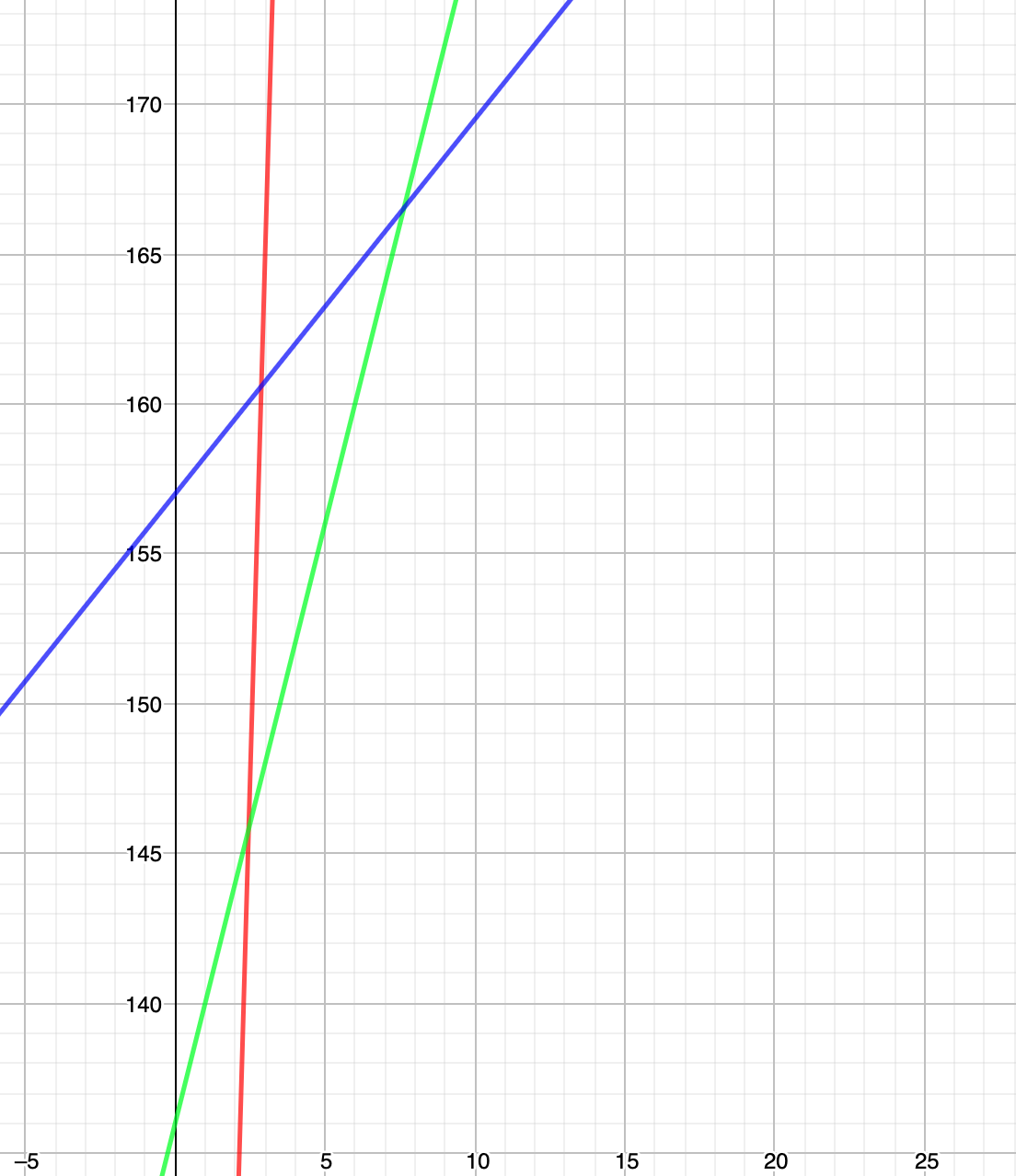
detailed
$$
60 + 35x \le 136 + 4x
$$

$$
x \le \frac{76}{31}
$$

$$
\because x \in Z^+
$$

$$
\therefore x \le 2
$$

when x less equals than 2, version 1 consume the leatest time

The rest are the same

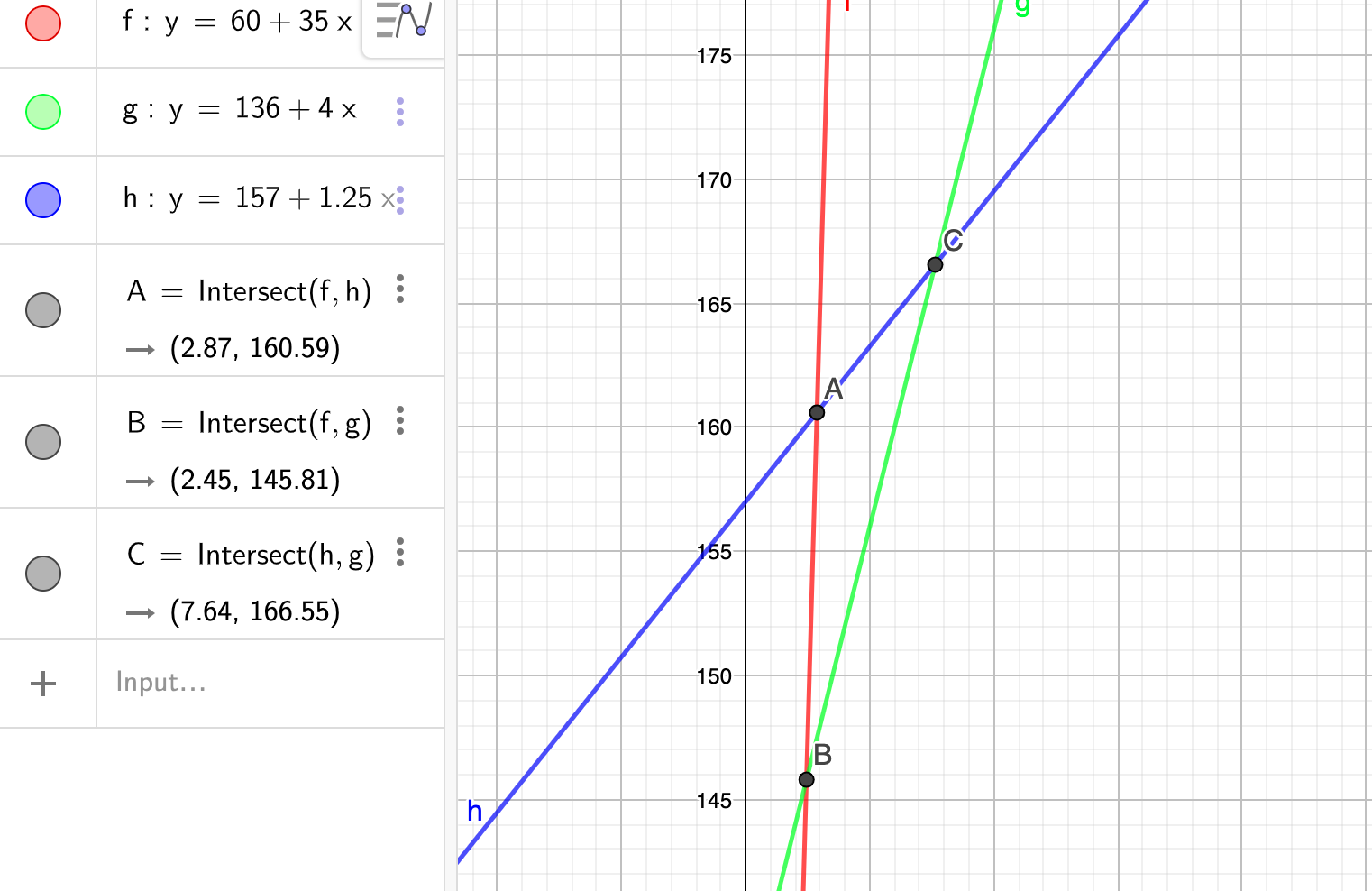
intersect
$$
\therefore \text{fastest version } = \begin{cases}
1 , & 0 \le x \le 2\
2 , & 3 \le x\le 7 \
3 , & x \ge 8
\end{cases}
$$

5.3 Program Example

To demonstrate how an abstract program can be systematically transformed into more efficient code, we will use a running example based on the vector data structure

1
2
3
4
5
/* Create abstract data type for vector */
 typedef struct {
 long len;
 data_t *data;
 } vec_rec, *vec_ptr;

We want to test multiple date type and different operations in C

1
2
3
typedef long /* int , float , double */ data_t;
#define IDENT 0 //1 //initial value for accumulation
#define OP + //*

Example program code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
/* Create vector of specified length */
vec_ptr new_vec(long len)
{
    /* Allocate header structure */
    vec_ptr result = (vec_ptr) malloc(sizeof(vec_rec));
    data_t *data = NULL;
    if (!result)
        return NULL;  /* Couldn't allocate storage */
    result->len = len;

    /* Allocate array */
    if (len > 0) {
        data = (data_t *)calloc(len, sizeof(data_t));
	if (!data) {
	    free((void *) result);
 	    return NULL; /* Couldn't allocate storage */
	}
    }
    /* data will either be NULL or allocated array */
    result->data = data;
    return result;
}

/* Free storage used by vector */
void free_vec(vec_ptr v) {
    if (v->data)
	free(v->data);
    free(v);
}

/*
 * Retrieve vector element and store at dest.
 * Return 0 (out of bounds) or 1 (successful)
 */
int get_vec_element(vec_ptr v, long index, data_t *dest)
{
    if (index < 0 || index >= v->len)
	return 0;
    *dest = v->data[index];
    return 1;
}

/* Return length of vector */
long vec_length(vec_ptr v)
{
    return v->len;
}
/* $end vec */


/* $begin get_vec_start */
data_t *get_vec_start(vec_ptr v)
{
    return v->data;
}
/* $end get_vec_start */

/*
 * Set vector element.
 * Return 0 (out of bounds) or 1 (successful)
 */
int set_vec_element(vec_ptr v, long index, data_t val)
{
    if (index < 0 || index >= v->len)
	return 0;
    v->data[index] = val;
    return 1;
}


/* Implementation with maximum use of data abstraction */
 void combine1(vec_ptr v, data_t *dest)
 {
 long i;
 *dest = IDENT;
     for (i = 0; i < vec_length(v); i++) {
         data_t val;
         get_vec_element(v, i, &val);
         *dest = *dest OP val;
     }
 }

In our experience, the best approach involves a combination of experimentation and analysis:

repeatedly attempting different approaches, performing measurements, and examining the assembly-code representations to identify underlying performance bottlenecks.

Run time of combine1

combine1

Finally I had to use /usr/bin/time --verbose /path/to/program to measure the performance

5.4 Eliminating Loop Inefficiencies

Oberserve that the length of vector doesn’t change during the loop, we can eliminate the function call of vec_length to reduce some instructions.

We modify combine1 as what we described above to get combine2

combine2

This optimization is an instance of a general class of optimizations known as code motion

  • They involve identifying a computation that is performed multiple times(within a loop) but the result don’t change
  • We can therefore move the computation to an earlier section of the code that does not get evaluated as often.

You think you won’t write codes like this ? Here is a very practical example.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/* Convert string to lowercase: slow */
void lower1(char *s)
{
long i;
for (i = 0; i < strlen(s); i++)
if (s[i] >= 'A' && s[i] <= 'Z')
s[i] -= ('A' - 'a');
}

 /* Convert string to lowercase: faster */
 void lower2(char *s)
 {
 long i;
 long len = strlen(s);

 for (i = 0; i < len; i++)
 if (s[i] >= 'A' && s[i] <= 'Z')
 s[i] -= ('A' - 'a');
 }

 /* Sample implementation of library function strlen */
 /* Compute length of string */
 size_t strlen(const char *s)
 {
 long length = 0;
 while (*s != '\0') {
 s++;
 length++;
 }
 return length;
 }

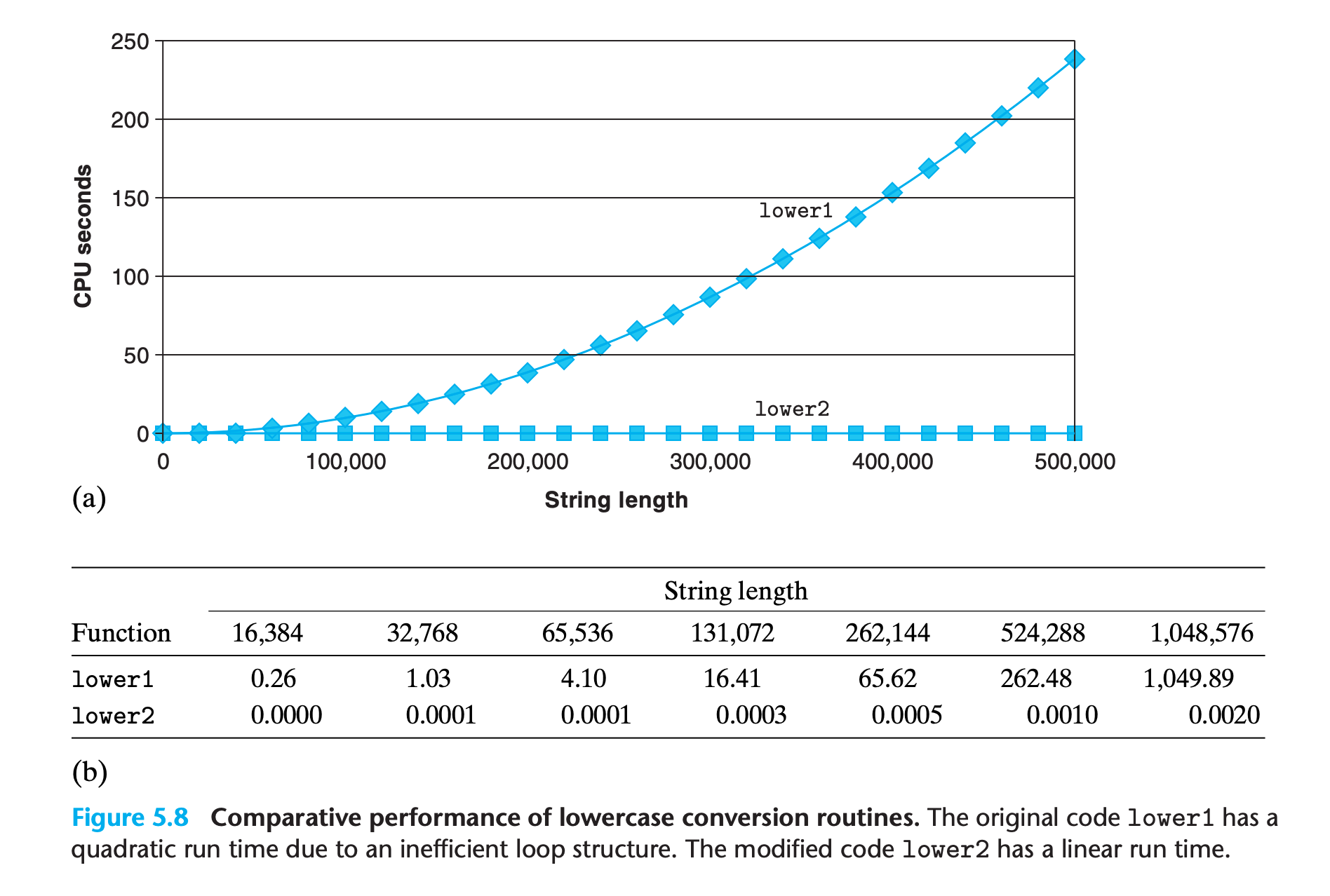
performance of lower

The compiler can’t do optimization for you in this case, since it need to know that even the content of string was changed the length of it will not. Even the most sophisticated compiler is unqualified.

Part of the job of a competent programmer is to avoid ever introducing such asymptotic inefficiency

Practice Problem 5.3

Consider the following functions:

1
2
3
4
long min(long x, long y) { return x < y ? x : y; }
long max(long x, long y) { return x < y ? y : x; }
void incr(long *xp, long v) { *xp += v; }
long square(long x) { return x*x; }

The following three code fragments call these functions:

1
2
3
4
5
6
7
8
A. for (i = min(x, y); i < max(x, y); incr(&i, 1))
t += square(i);
B. for (i = max(x, y) - 1; i >= min(x, y); incr(&i, -1))
t += square(i);
C. long low = min(x, y);
long high = max(x, y);
for (i = low; i < high; incr(&i, 1))
t += square(i);

Assume x equals 10 and y equals 100.

Fill in the following table indicating the number of times each of the four functions is called in code fragments A–C:

Code min max incr square
A
B
C

My solution : :white_check_mark:

Beware that the function used as condition will be call one more time when quiting the loop

Code min max incr square
A 1 91 90 90
B 91 1 90 90
C 1 1 90 90

The subtle difference is critical to performance

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <stdio.h>
#include <time.h>
long min(long x, long y) { return x < y ? x : y; }
long max(long x, long y) { return x < y ? y : x; }
void incr(long *xp, long v) { *xp += v; }
long square(long x) { return x*x; }

int main(){
    clock_t start , end;
    long i ;
    long x = 1 , y = 100000 ;
    long t = 0; 
    start = clock();
    for (i = min(x, y); i < max(x, y); incr(&i, 1))
        t += square(i);
    end = clock();
    printf("time consumed by A : %lf\n" ,(double)(end - start)/CLOCKS_PER_SEC );
    t = 0;
    start = clock();
    for (i = max(x, y) - 1; i >= min(x, y); incr(&i, -1))
        t += square(i);
    end = clock();
    printf("time consumed by B : %lf\n" ,(double)(end - start)/CLOCKS_PER_SEC );

    start = clock();
    long low = min(x, y);
    long high = max(x, y);
    for (i = low; i < high; incr(&i, 1))
        t += square(i);
    end = clock();
    printf("time consumed by C : %lf\n" ,(double)(end - start)/CLOCKS_PER_SEC );
}
/*
time consumed by A : 0.000430
time consumed by B : 0.000418
time consumed by C : 0.000269
*/

5.5 Reducing Procedure Calls

We can see in the code for combine2 that get_ vec_element is called on every loop iteration to retrieve the next vector element.

  • A simple analysis of the code for combine2 shows that all references will be valid, so we can remove bound check
  • Rather than making a function call to retrieve each vector element, we can accesses the array directly

No improve

However, performance doesn’t improve at all!

  • The modification we have made is not wise
  • In principle, the user of the vector abstract data type should not even need to know that the vector contents are stored as an array, rather than as some other data structure such as a linked list.
  • A purist might say that this transformation seriously impairs the program modularity

So why would this happen? See 5.11.2

5.6 Eliminating Unneeded Memory References

In combine3 

1
2
3
4
5
6
7
8
9
10
11
void combine3(vec_ptr v, data_t *dest)
 {
 long i;
 long length = vec_length(v);
 data_t *data = get_vec_start(v);

 *dest = IDENT;
 for (i = 0; i < length; i++) {
 *dest = *dest OP data[i];
 }
 }

We can see that memory pointed by dest are referred mulitple times

1
2
3
4
5
6
7
8
9
#Inner loop of combine3. data_t = double, OP = *
#dest in %rbx, data+i in %rdx, data+length in %rax
 .L17: loop:
 vmovsd (%rbx), %xmm0 #Read product from dest
 vmulsd (%rdx), %xmm0, %xmm0 #Multiply product by data[i]
 vmovsd %xmm0, (%rbx) #Store product at dest
 addq $8, %rdx #Increment data+i
 cmpq %rax, %rdx #Compare to data+length
 jne .L17 #If !=, goto loop

This reading and writing is wasteful, since the value read from dest at the beginning of each iteration should simply be the value written at the end of the previous iteration

We should use a temp variable(a register) to accumulate the value

1
2
3
4
5
6
7
#Inner loop of combine4. data_t = double, OP = *
#acc in %xmm0, data+i in %rdx, data+length in %rax
 .L25: loop:
 vmulsd (%rdx), %xmm0, %xmm0 #Multiply acc by data[i]
 addq $8, %rdx #Increment data+i
 cmpq %rax, %rdx #Compare to data+length
 jne .L25 #If !=, goto loop
1
2
3
4
5
6
7
8
9
10
11
12
13
/* Accumulate result in local variable */
void combine4(vec_ptr v, data_t *dest)
{
long i;
long length = vec_length(v);
data_t *data = get_vec_start(v);
data_t acc = IDENT;

for (i = 0; i < length; i++) {
 acc = acc OP data[i];
 }
 *dest = acc;
 }

significant improvement

Again, the compiler cannot optimize the code automatically, since the hazard of memory alias. For example

1
2
3
v = [2,3,4];
combine3(v, get_vec_start(v) + 2); //v = [2,3,36]
combine4(v, get_vec_start(v) + 2); //v = [2,3,24]

Practice Problem 5.4

When we use gcc to compile combine3 with command-line option -O2, we get code with substantially better CPE performance than with -O1:

problem picture

We achieve performance comparable to that for combine4, except for the case of integer sum, but even it improves significantly. On examining the assembly code generated by the compiler, we find an interesting variant for the inner loop:

1
2
3
4
5
6
7
8
9
#Inner loop of combine3. data_t = double, OP = *. Compiled -O2
#dest in %rbx, data+i in %rdx, data+length in %rax
#Accumulated product in %xmm0
.L22: loop:
vmulsd (%rdx), %xmm0, %xmm0 #Multiply product by data[i]
addq $8, %rdx #Increment data+i
cmpq %rax, %rdx #Compare to data+length
vmovsd %xmm0, (%rbx) #Store product at dest
jne .L22 #If !=, goto loop

We can compare this to the version created with optimization level 1:

1
2
3
4
5
6
7
8
9
#Inner loop of combine3. data_t = double, OP = *. Compiled -O1
#dest in %rbx, data+i in %rdx, data+length in %rax
.L17: loop:
vmovsd (%rbx), %xmm0 #Read product from dest
vmulsd (%rdx), %xmm0, %xmm0 #Multiply product by data[i]
vmovsd %xmm0, (%rbx) #Store product at dest
addq $8, %rdx #Increment data+i
cmpq %rax, %rdx #Compare to data+length
jne .L17 #If !=, goto loop

We see that, besides some reordering of instructions, the only difference is that the more optimized version does not contain the vmovsd implementing the read from the location designated by dest

A. How does the role of register %xmm0 differ in these two loops?

B. Will the more optimized version faithfully implement the C code of combine3, including when there is memory aliasing between dest and the vector data?

C. Either explain why this optimization preserves the desired behavior, or give an example where it would produce different results than the less optimized code.

My solution : :white_check_mark:

A:

In combine3 -O2, %xmm0 serves as the result of each iteration

In combine3 -O1, %xmm0 serves as the read destination.

B:

Yes

C:

Because the optimized code actually do the write back, keeping the value at dest up-to-date

5.7 Understanding Modern Processors

One of the remarkable feats of modern microprocessors is that they employ complex and exotic microarchitectures, in which multiple instructions can be executed in parallel, while presenting an operational view of simple sequential instruction execution.(Called instruction-level-parallelism)

We will find that two different lower bounds characterize the maximum performance of a program

  • Latency
  • Throughput

5.7.1 Overall Operation

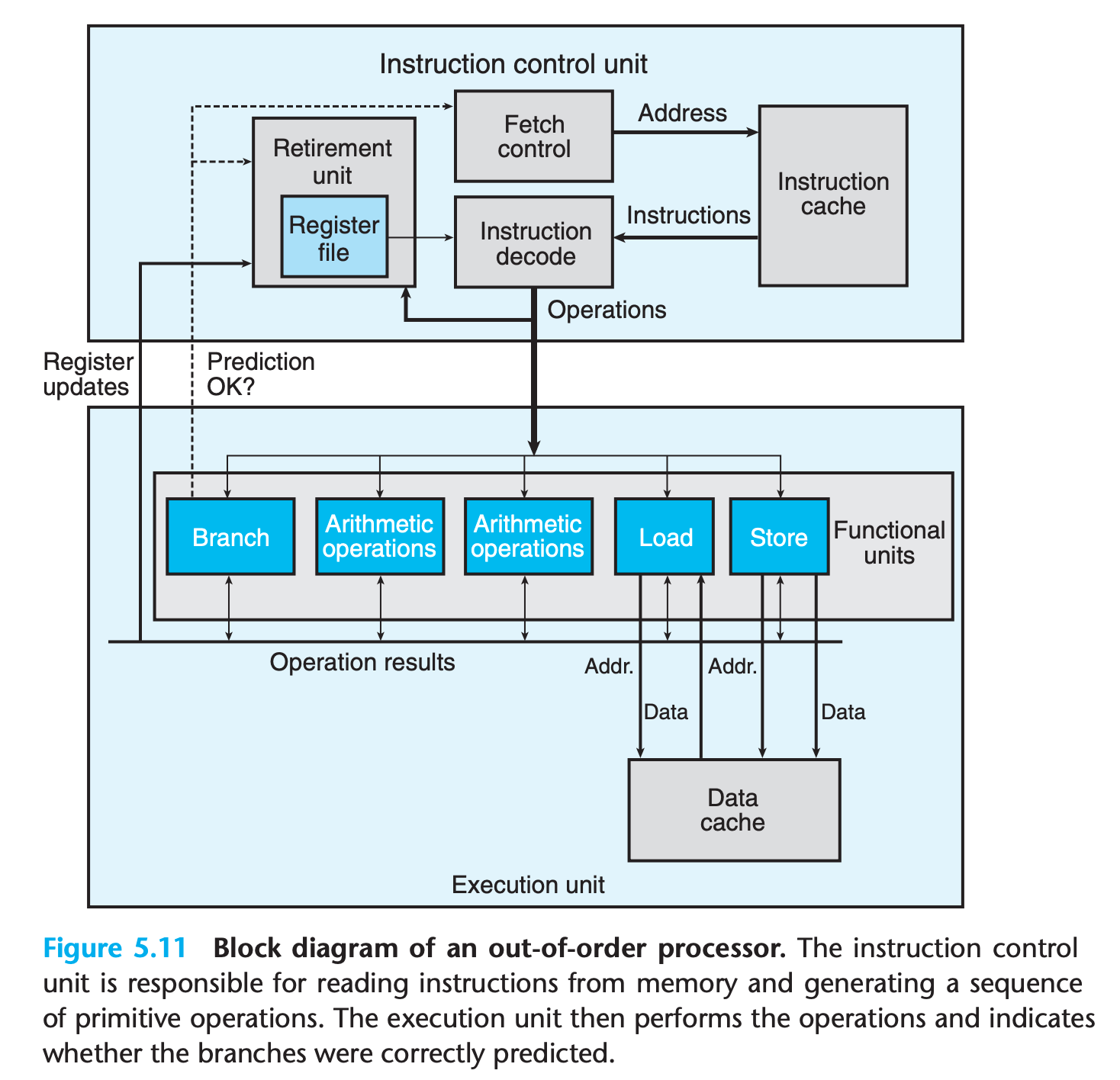
layout of mordern processor

The overall design has two main parts:

  • The instruction control unit (ICU), which is responsible for reading a sequence of instructions from memory and generating from these a set of primitive operations(sometimes referred to as micro-operations) to perform on program data

    1
    2
    3
    4
    5
    6
    7
    # For complex instruction machine
    addq %rax,%rdx  -> a simple add operation

    addq %rax,8(%rdx) -> three micro-operations
                      -> read from memory M[8+%rdx]
                      -> addition
                      -> store the result to memory

  • The execution unit (EU), which then executes these operations.

    Compared to the simple in-order pipeline we studied in Chapter 4, out-of-order processors require far greater and more complex hardware, but they are better at achieving higher degrees of instruction-level parallelism.

Within the ICU, the retirement unit keeps track of the ongoing processing and makes sure that it obeys the sequential semantics of the machine-level program.

  • Once the operations for the instruction have completed and any branch points leading to this instruction are confirmed as having been correctly predicted, the instruction can be retired, with any updates to the program registers being made.
  • If some branch point leading to this instruction was mispredicted, on the other hand, the instruction will be flushed, discarding any results that may have been computed. By this means, mispredictions will not alter the program state.

Also, a technique call register renaming is used to implement function like data-forwarding

5.7.2 Functional Unit Performance

Hardware limit the ultimate performance of programs

hardware bound

5.7.3 An Abstract Model of Processor Operation

we will use a data-flow representation of programs, a graphical notation showing how the data dependencies between the different operations constrain the order in which they are executed

These constraints then lead to critical paths in the graph, putting a lower bound on the number of clock cycles required to execute a set of machine instructions.

From Machine-Level Code to Data-Flow Graphs

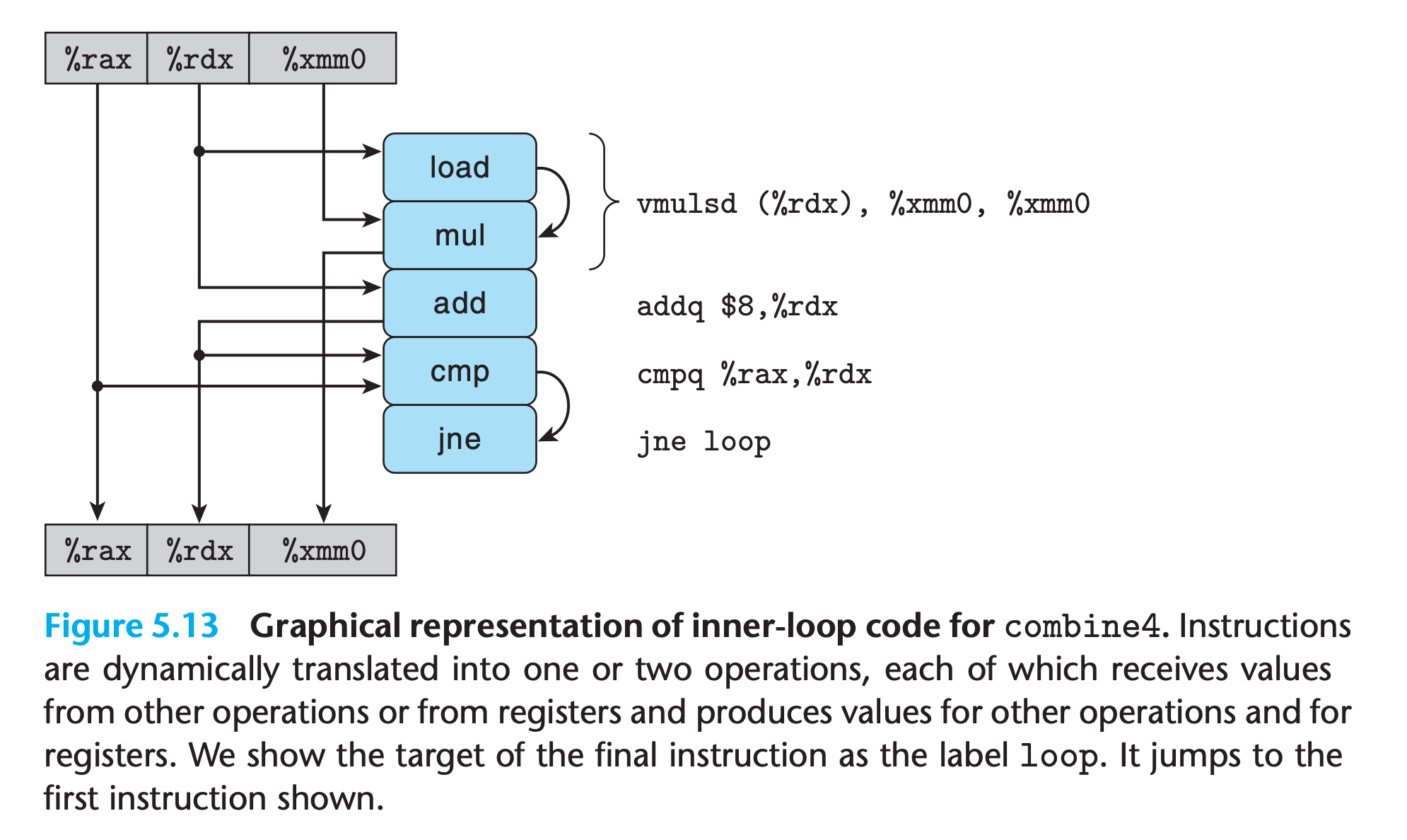
data flow

The registers at top store values before execution, those at the bottom store values after execution

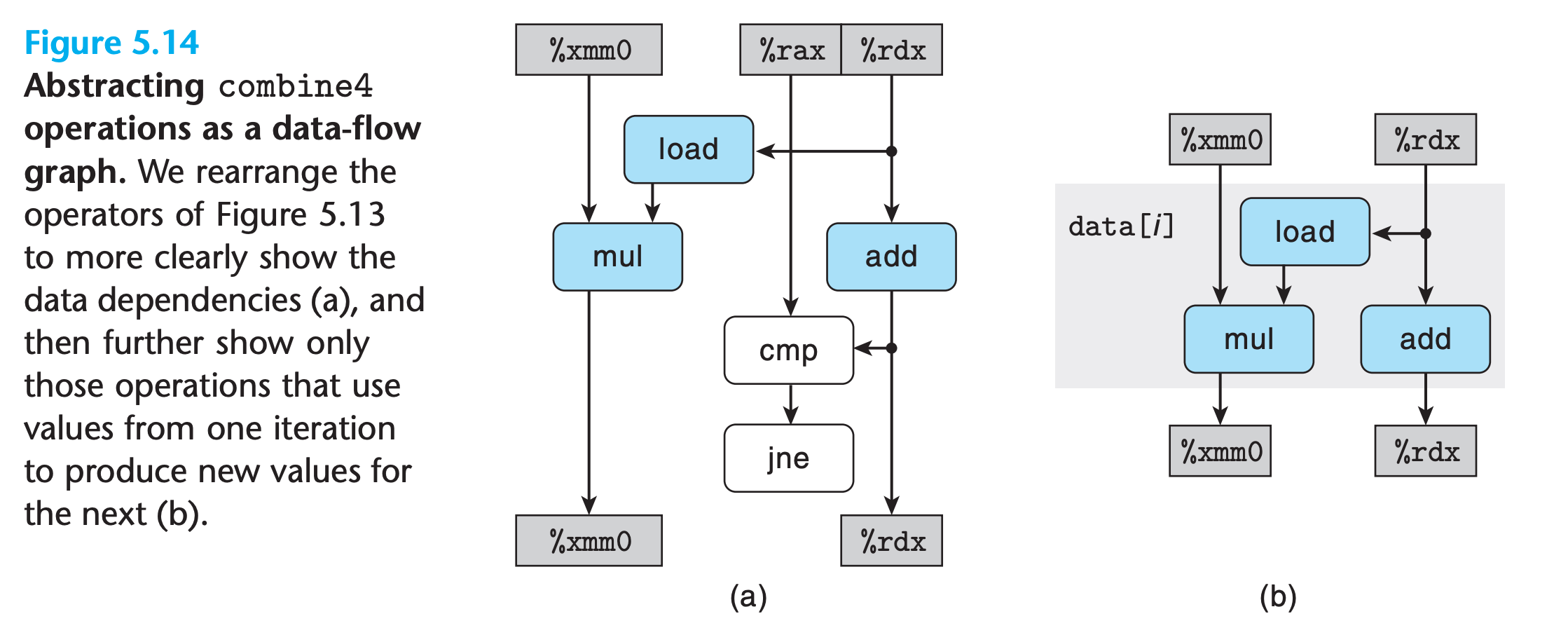
abstract graph

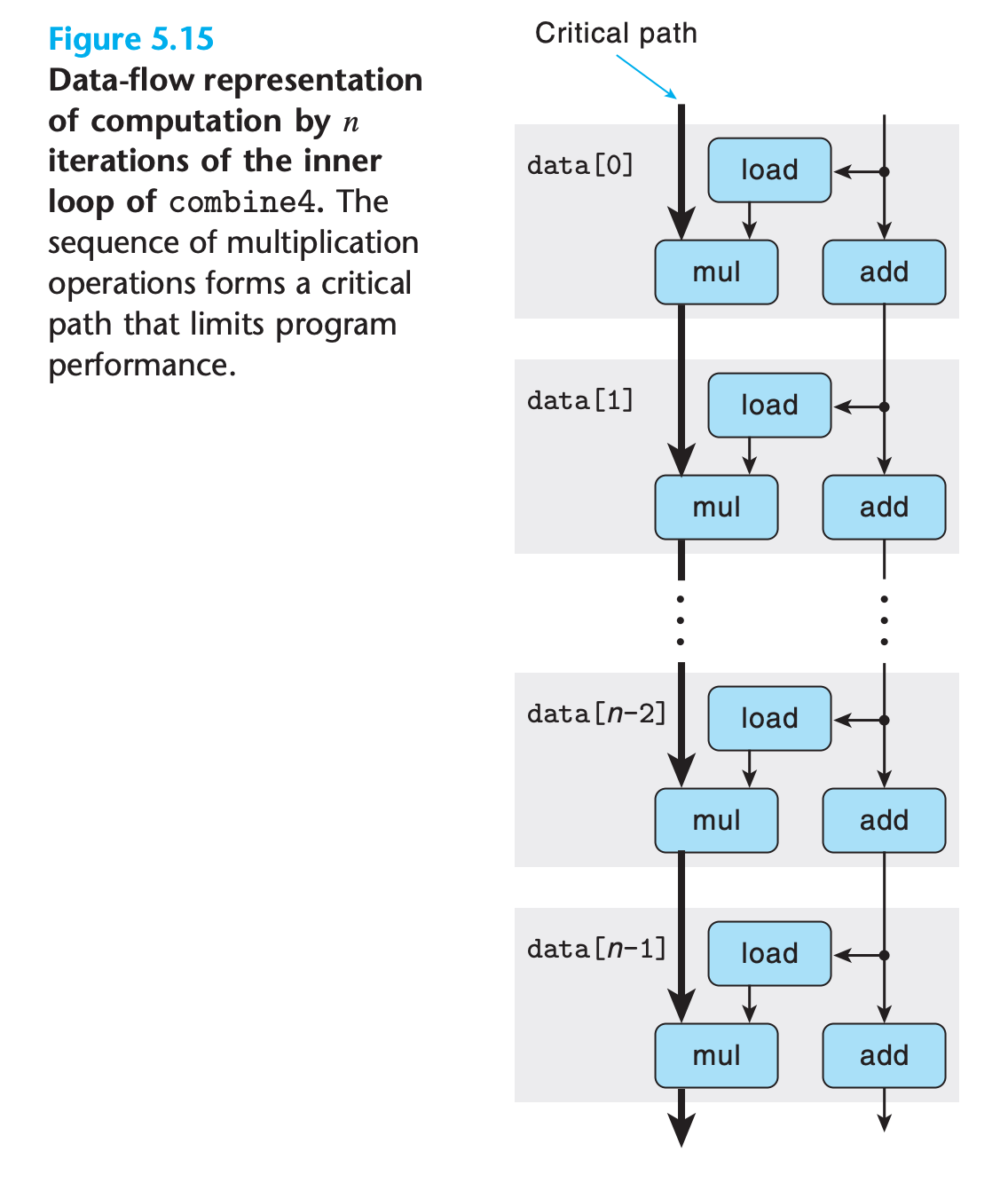
critical path

The left chain needs 5n clocks while the right chain needs only n clocks

So when executing the function, the floating-point multiplier becomes the limiting resource.

The other operations required during the loop—manipulating and testing pointer value data+i and reading data from memory—proceed in parallel with the multiplication. As each successive value of acc is computed, it is fed back around to compute the next value, but this will not occur until 5 cycles later

Other Performance Factors

Other factors can also limit performance, including the total number of functional units available and the number of data values that can be passed among the functional units on any given step.

Our next task will be to restructure the operations to enhance instruction-level parallelism. We want to transform the program in such a way that our only limitation becomes the throughput bound, yielding CPEs below or close to 1.00.

Practice Problem 5.5

Suppose we wish to write a function to evaluate a polynomial, where a polynomial of degree n is defined to have a set of coefficients $a_0, a_1, a_2,…,a_n$. For a value x, we evaluate the polynomial by computing
$$
a_0 + a_1x + a_2x_2 + … + a_nx_n
$$
This evaluation can be implemented by the following function, having as arguments an array of coefficients a, a value x, and the polynomial degree degree (the value n in Equation 5.2). In this function, we compute both the successive terms of the equation and the successive powers of x within a single loop:

1
2
3
4
5
6
7
8
9
10
11
double poly(double a[], double x, long degree)
{
long i;
double result = a[0];
double xpwr = x; /* Equals x^i at start of loop */
for (i = 1; i <= degree; i++) {
result += a[i] * xpwr;
xpwr = x * xpwr;
}
 return result;
 }

A. For degree n, how many additions and how many multiplications does this code perform?

B. On our reference machine, with arithmetic operations having the latencies shown in Figure 5.12, we measure the CPE for this function to be 5.00. Explain how this CPE arises based on the data dependencies formed between iterations due to the operations implementing lines 7–8 of the function.

My solution :

A : n addition and 2n multiplication

B : the two multiplication can run in parallel

Solution on the book:

B. We can see that the performance-limiting computation here is the repeated computation of the expression xpwr = x * xpwr. This requires a floatingpoint multiplication (5 clock cycles), and the computation for one iteration cannot begin until the one for the previous iteration has completed. The updating of result only requires a floating-point addition (3 clock cycles) between successive iterations.

Practice Problem 5.6

$$
a_0 + x(a_1 + x(a_2 + … + x(a_{n−1} + xa_n) …))
$$

Using Horner’s method, we can implement polynomial evaluation using the following code:

1
2
3
4
5
6
7
8
9
/* Apply Horner’s method */
double polyh(double a[], double x, long degree)
{
    long i;
    double result = a[degree];
    for (i = degree-1; i >= 0; i--)
    result = a[i] + x*result;
    return result;
}

A. For degree n, how many additions and how many multiplications does this code perform?

B. On our reference machine, with the arithmetic operations having the latencies shown in Figure 5.12, we measure the CPE for this function to be 8.00. Explain how this CPE arises based on the data dependencies formed between iterations due to the operations implementing line 7 of the function.

C. Explain how the function shown in Practice Problem 5.5 can run faster, even though it requires more operations.

My solution :

A : n addition and n multiplication

B : addition must wait for multiplication to complete

C : in 5.5 the two multiplication can run in parallel

Solution on the book :

B. We can see that the performance-limiting computation here is the repeated computation of the expression result = a[i] + x*result. Starting from the value of result from the previous iteration, we must first multiply it by x (5 clock cycles) and then add it to a[i] (3 cycles) before we have the value for this iteration. Thus, each iteration imposes a minimum latency of 8 cycles, exactly our measured CPE.

C. Although each iteration in function poly requires two multiplications rather than one, only a single multiplication occurs along the critical path per iteration.

Verification :

“Better algorithm” does not guarantee a better performance !!!

Reduce data dependency really matters !!!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#define N 50000
union data {
    double d;
    int i[2];
};
typedef union data Data;
Data array [N];
double poly(Data a[], double x, long degree)
{
long i;
double result = a[0].d;

double xpwr = x; /* Equals x^i at start of loop */
for (i = 1; i <= degree; i++) {
result += a[i].d * xpwr;
xpwr = x * xpwr;
}
 return result;
 }

/* Apply Horner’s method */
double polyh(Data a[], double x, long degree)
{
    long i;
    double result = a[degree].d;
    for (i = degree-1; i >= 0; i--)
    result = a[i].d + x*result;
    return result;
}

#include <stdio.h>
#include <time.h>
#include <stdlib.h>
int main(){
    clock_t start , end ;
    for (int x = 0 ; x < N ; x++){
       array[x].i[0] = rand();
       array[x].i[1] = rand();
    }
    start = clock();
    poly(array, 3.14, N-1);
    end = clock();
    printf("Normal method cost : %f\n" , (double)(end - start) / CLOCKS_PER_SEC );

    start = clock();
    polyh(array, 3.14, N-1);
    end = clock();
    printf("Horner method cost : %f\n" , (double)(end - start) / CLOCKS_PER_SEC );

    printf("\n");
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
$ for ((i = 0 ; i < 10 ; i++)) ./test
Normal method cost : 0.000356
Horner method cost : 0.000468

Normal method cost : 0.000271
Horner method cost : 0.000363

Normal method cost : 0.000270
Horner method cost : 0.000363

Normal method cost : 0.000272
Horner method cost : 0.000363

Normal method cost : 0.000274
Horner method cost : 0.000364

Normal method cost : 0.000271
Horner method cost : 0.000377

Normal method cost : 0.000271
Horner method cost : 0.000363

Normal method cost : 0.000270
Horner method cost : 0.000421

Normal method cost : 0.000271
Horner method cost : 0.000363

Normal method cost : 0.000270
Horner method cost : 0.000371

(I once thought that it is the data cache resulted in the improvement, but reverse the order of function call gives the same result)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
Horner method cost : 0.002377
Normal method cost : 0.001744

Horner method cost : 0.002086
Normal method cost : 0.001518

Horner method cost : 0.002103
Normal method cost : 0.001516

Horner method cost : 0.002077
Normal method cost : 0.001515

Horner method cost : 0.001997
Normal method cost : 0.001588

Horner method cost : 0.002050
Normal method cost : 0.001586

Horner method cost : 0.002063
Normal method cost : 0.001590

Horner method cost : 0.002004
Normal method cost : 0.001546

Horner method cost : 0.002153
Normal method cost : 0.001608

Horner method cost : 0.002253
Normal method cost : 0.001552

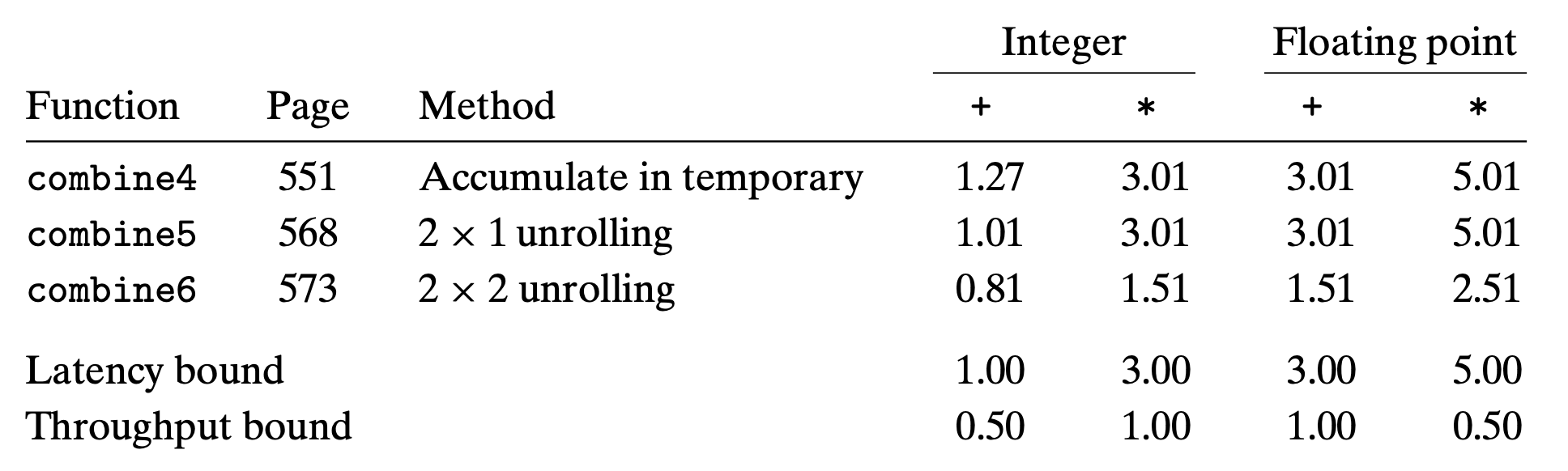
5.8 Loop Unrolling

Loop unrolling is a program transformation that reduces the number of iterations for a loop by increasing the number of elements computed on each iteration

Loop unrolling can improve performance in two ways

  • It reduces the number of operations that do not contribute directly to the program result, such as loop indexing and conditional branching.
  • We can further transform the code to reduce the number of operations in the critical paths of the overall computation.

k × 1 loop unrolling strategy

processing k elements in one loop

  • upper limit to be i < n − k + 1 to prevent out-of-bound reference(from i to i+k-1 in each iteration,i+k-1 < n )
  • Loop index i is incremented by k in each iteration
  • We include the second loop to step through the final few elements of the vector one at a time. The body of this loop will be executed between 0 and k − 1 times.
  • For example when k == 2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/* 2 x 1 loop unrolling */
void combine5(vec_ptr v, data_t *dest)
{
long i;
long length = vec_length(v);
long limit = length-1;
data_t *data = get_vec_start(v);
data_t acc = IDENT;

 /* Combine 2 elements at a time */
 for (i = 0; i < limit; i+=2) {
 acc = (acc OP data[i]) OP data[i+1];
 }

 /* Finish any remaining elements */
 for (; i < length; i++) {
 acc = acc OP data[i];
 }
 *dest = acc;
 }
//Applying 2 × 1 loop unrolling. This transformation can reduce the effect of loop overhead.

Practice Problem 5.7 :white_check_mark:

Modify the code for combine5 to unroll the loop by a factor k = 5.

My solution :

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/* 5 x 1 loop unrolling */
void mycombine5(vec_ptr v, data_t *dest)
{
long i;
long length = vec_length(v);
long limit = length-4;  // i + 5 - 1 < len
data_t *data = get_vec_start(v);
data_t acc = IDENT;

 /* Combine 2 elements at a time */
 for (i = 0; i < limit; i+=5) {
 acc = ((((acc OP data[i]) OP data[i+1]) OP data[i+2]) OP data[i+3]) OP data[i+4];
 //data dependency here, but in case of OP be float point number operation, we can not compute (data[i+2] OP data[i+3]) first. Beware of the rounding, float point is not associative !!!
 }

 /* Finish any remaining elements */
 for (; i < length; i++) {
 acc = acc OP data[i];
 }

 *dest = acc;
 }

Verification:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
time consumed by combine5 : 0.000861
time consumed by mycombine5: 0.000692

time consumed by combine5 : 0.000839
time consumed by mycombine5: 0.000688

time consumed by combine5 : 0.000894
time consumed by mycombine5: 0.000754

time consumed by combine5 : 0.000899
time consumed by mycombine5: 0.000760

time consumed by combine5 : 0.000942
time consumed by mycombine5: 0.000828

time consumed by combine5 : 0.000903
time consumed by mycombine5: 0.000796

time consumed by combine5 : 0.000911
time consumed by mycombine5: 0.000768

time consumed by combine5 : 0.000959
time consumed by mycombine5: 0.000701

time consumed by combine5 : 0.000837
time consumed by mycombine5: 0.000695

time consumed by combine5 : 0.000860
time consumed by mycombine5: 0.000705

(reverse function call order is done to ensure the improvement is not caused by cache)

Solution on the book does not solve data dependency either.

==Loop unrolling can easily be performed by a compiler==. Many compilers do this as part of their collection of optimizations. gcc will perform some forms of loop unrolling when invoked with optimization level 3 or higher

We see that the CPE for integer addition improves, achieving the latency bound of 1.00

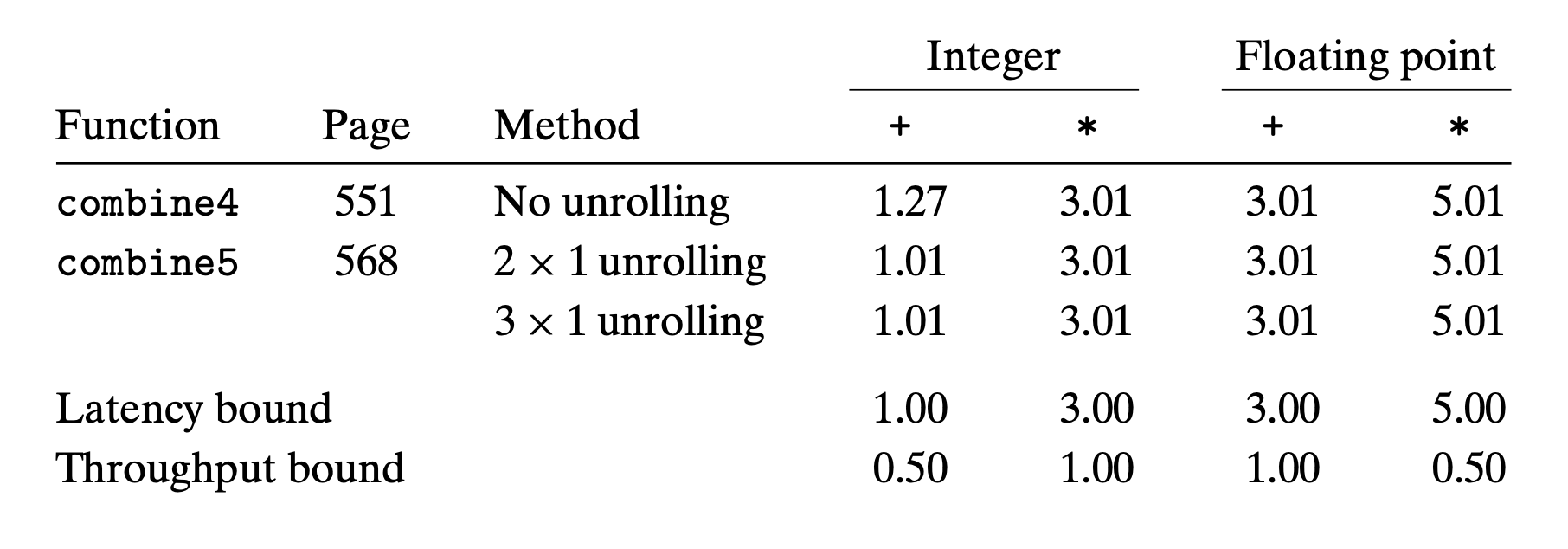
combine5 performance

By reducing the number of overhead operations relative to the number of additions required to compute the vector sum, we can reach the point where the 1-cycle latency of integer addition becomes the performancelimiting factor.

On the other hand, none of the other cases improve—they are already at their latency bounds

By examining the machine-level code, we can see that there is still a critical path of n multiplication operations —there are half as many iterations, but each iteration has two multiplication operations in sequence

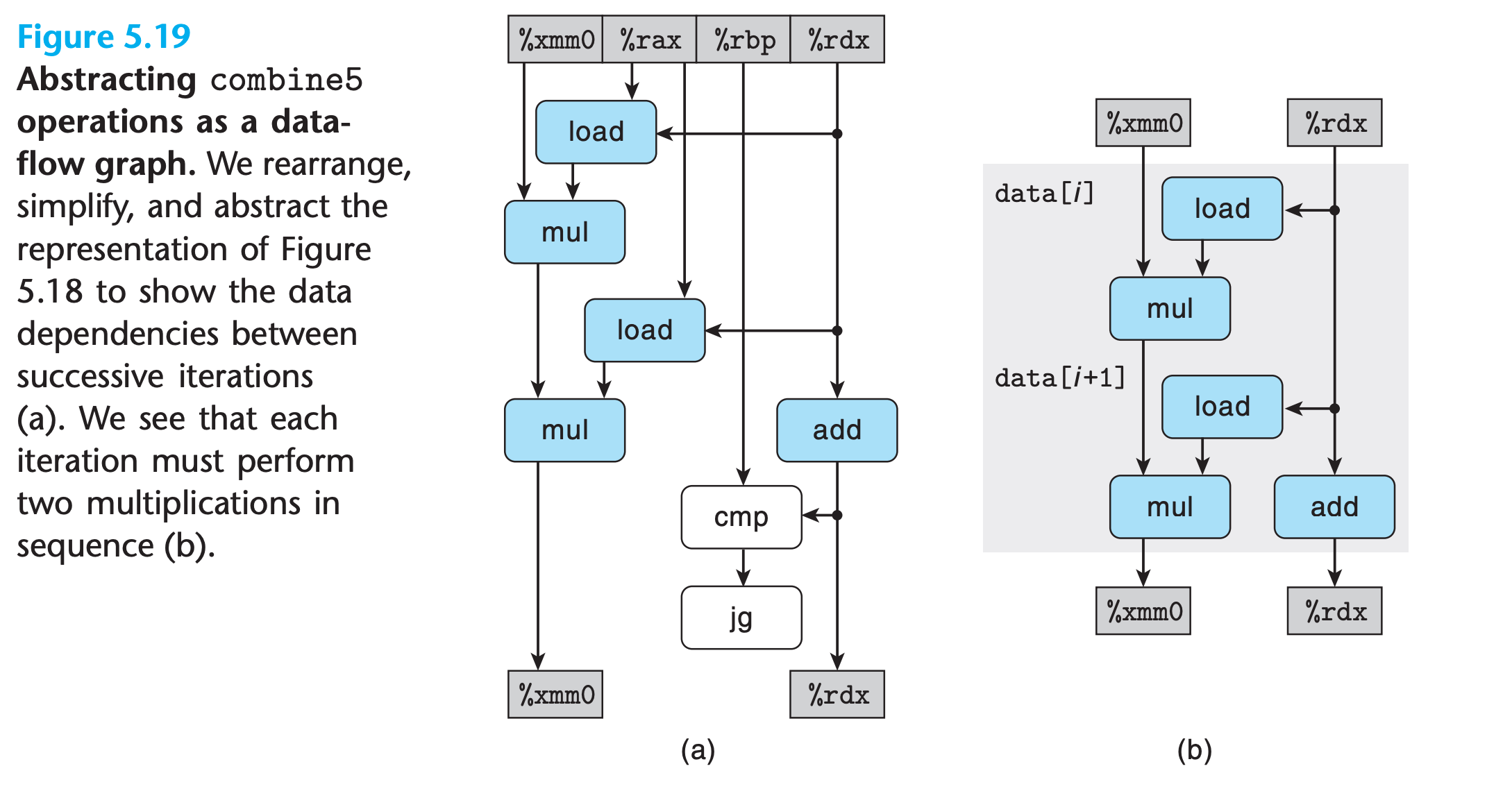
combine5 data dependancy graph

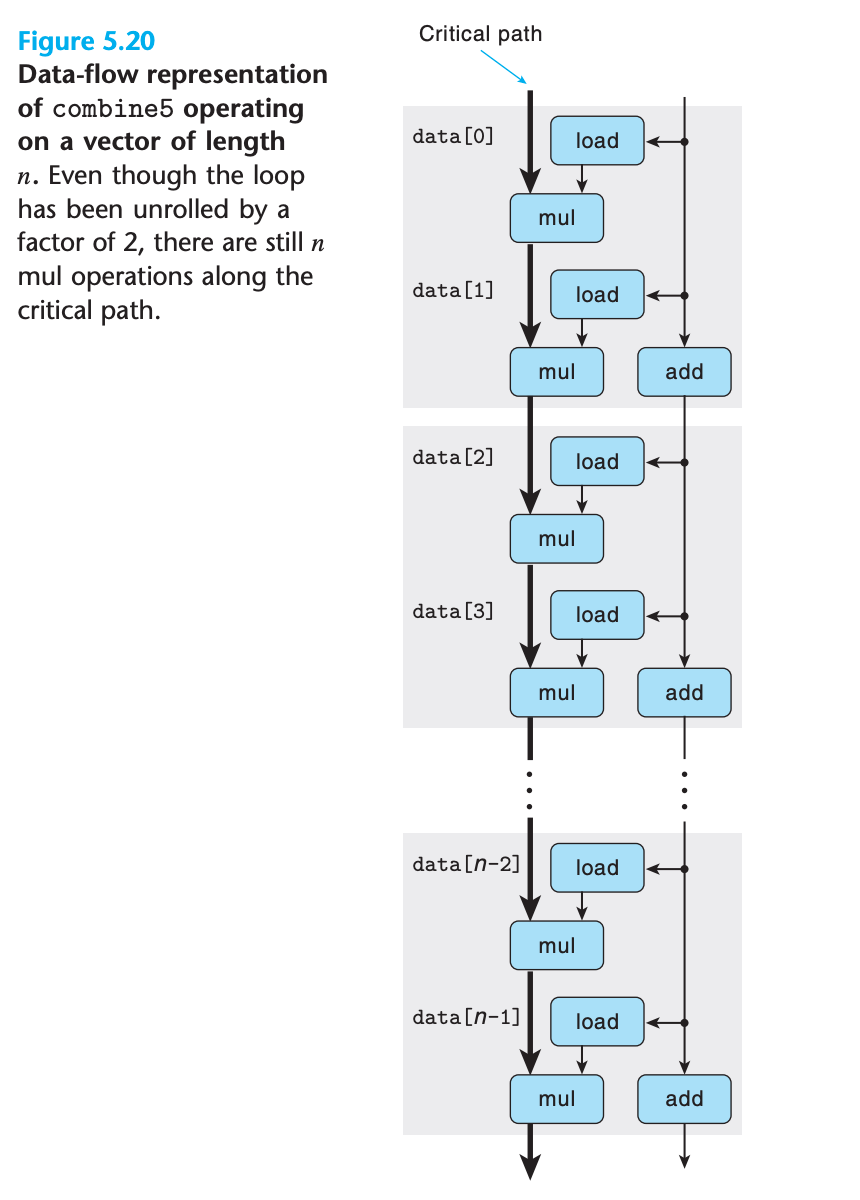
data flow of combine 5

5.9 Enhancing Parallelism

The functional units performing addition and multiplication are all fully pipelined, meaning that they can start new operations every clock cycle, and some of the operations can be performed by multiple functional units.

We will now investigate ways to break sequential dependency and get performance better than the latency bound.

5.9.1 Multiple Accumulators

For a combining operation that is ==associative and commutative==, such as integer addition or multiplication, we can improve performance by splitting the set of combining operations into two or more parts and combining the results at the end.

For example for n elements:

1
2
3
4
5
result = n1 * n2 * n3 ... * n;

result = n_even * n_odd;
n_even = n2 * n4 * n6 ...;
n_odd = n1 * n3 * n5 ...;

We call this $2 \times 2 $ loop unrolling, 2 elements per iteration and 2 elements operate parallelly.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/* 2 x 2 loop unrolling */
void combine6(vec_ptr v, data_t *dest)
{
long i;
long length = vec_length(v);
long limit = length-1;
data_t *data = get_vec_start(v);
data_t acc0 = IDENT;
data_t acc1 = IDENT;

 /* Combine 2 elements at a time */
 for (i = 0; i < limit; i+=2) {
 acc0 = acc0 OP data[i];
 acc1 = acc1 OP data[i+1];
 }

 /* Finish any remaining elements */
 for (; i < length; i++) {
 acc0 = acc0 OP data[i];
 }
 *dest = acc0 OP acc1;
 }

combine6 performance

(I suppose the arithmetic result of floating point is not correct here)

The processor no longer needs to delay the start of one sum or product operation until the previous one has completed.

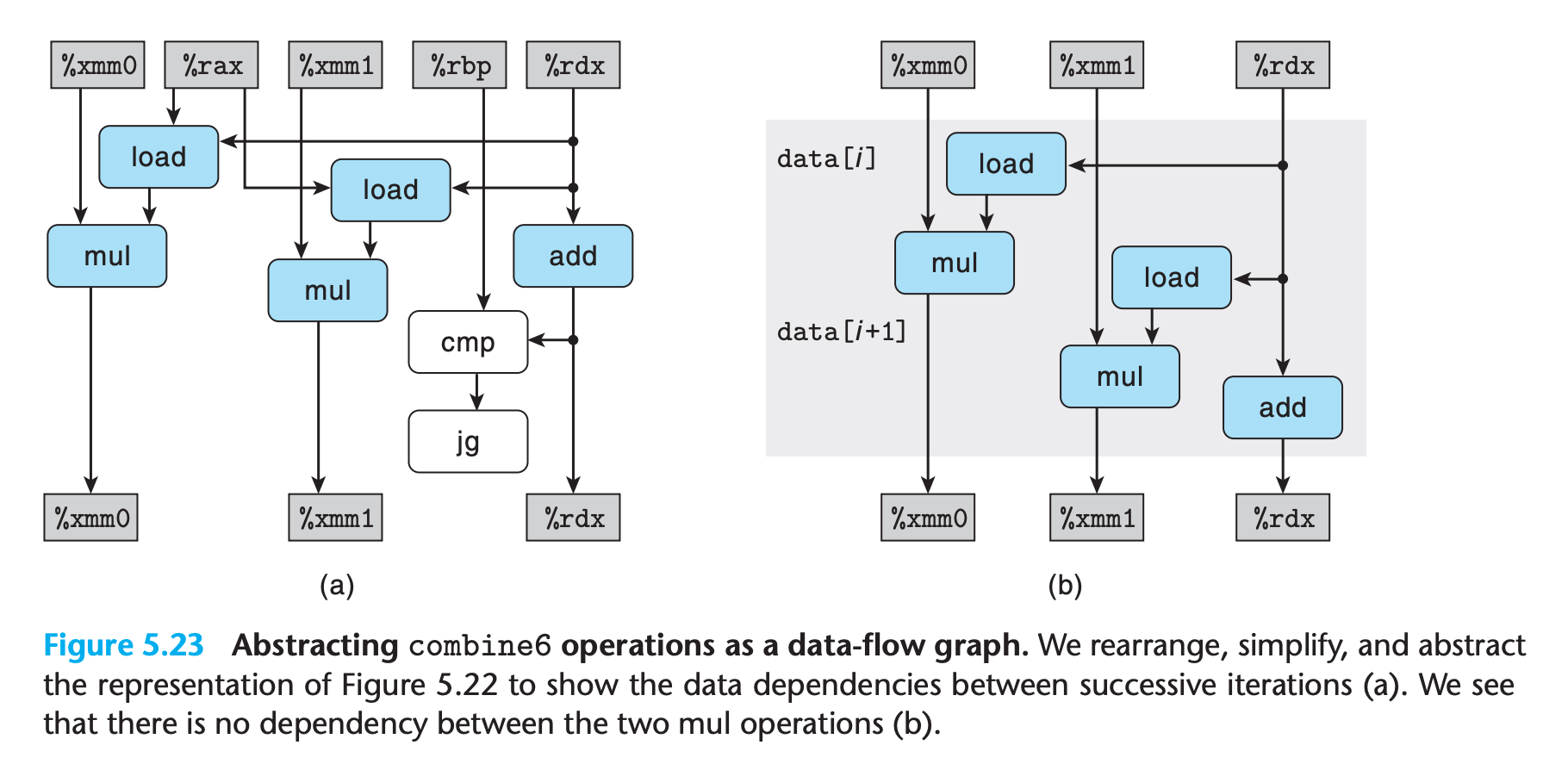
data flow of combine6

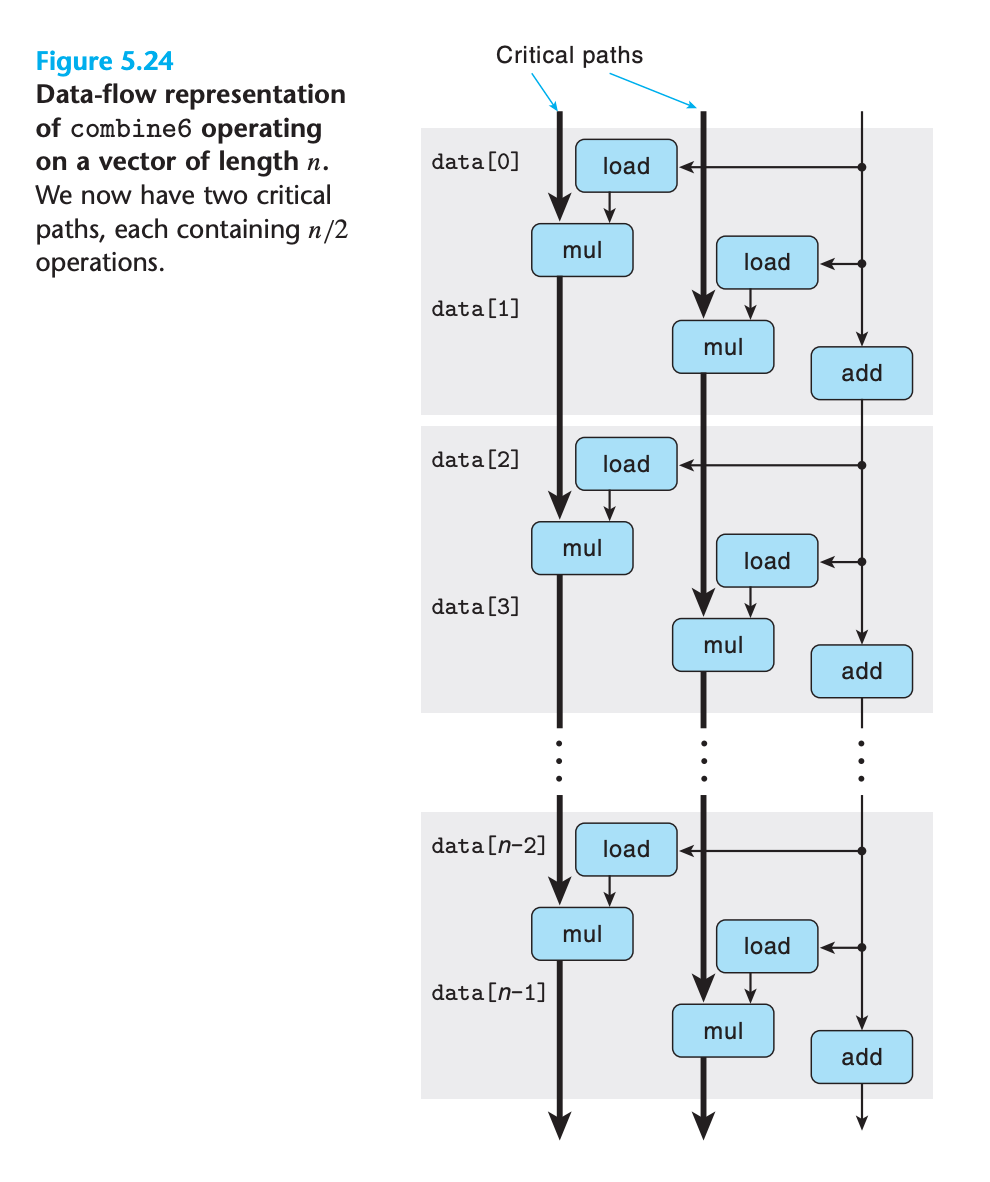
critical path length reduced by factor of 2

We see that we now have two critical paths run in parallel, so data dependency is reduced.

We can generalize the multiple accumulator transformation to unroll the loop by a factor of k and accumulate k values in parallel, yielding k × k loop unrolling.

We can see that, for sufficiently large values of k, the program can achieve nearly the throughput bounds for all cases.

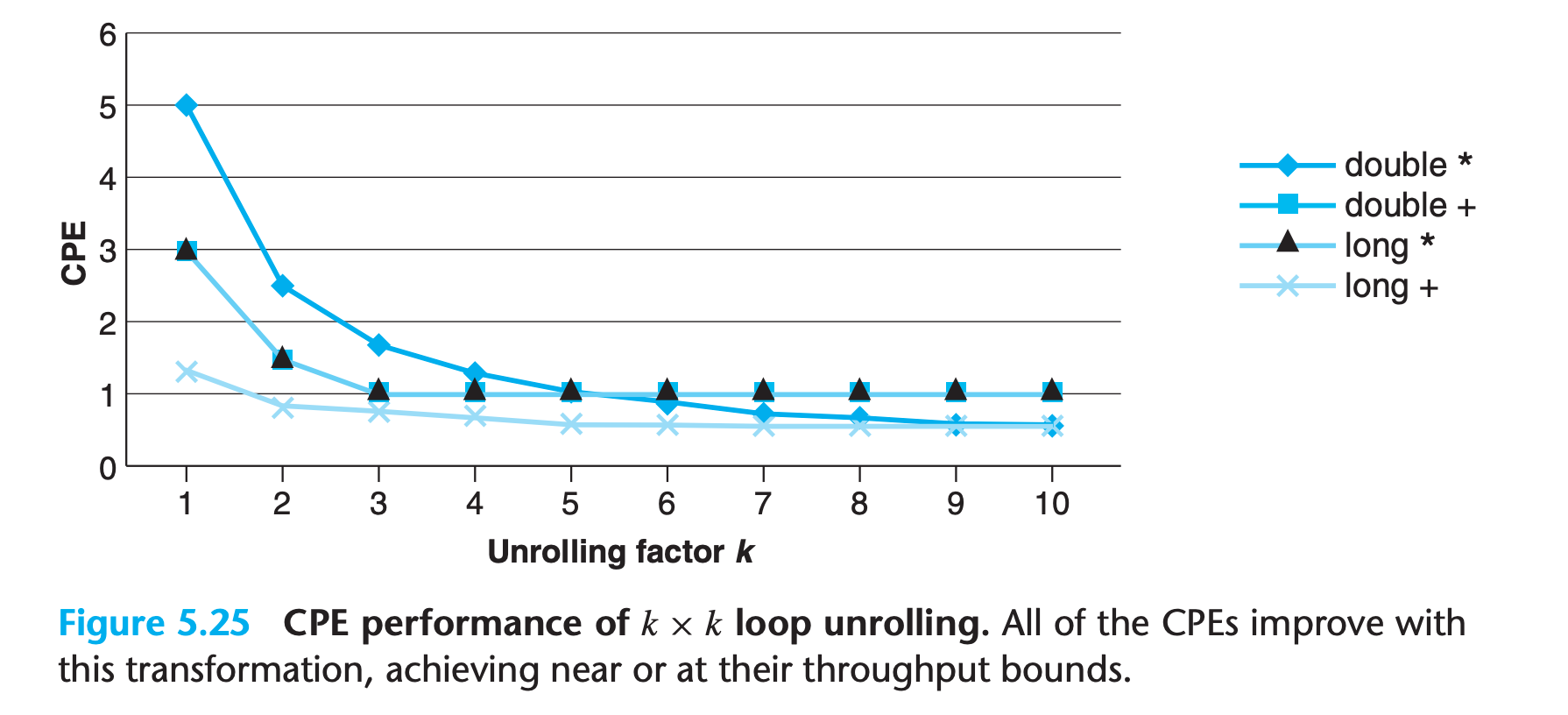
achieve throughput

In performing the k × k unrolling transformation, we must consider whether it preserves the functionality of the original function

  • We have seen in Chapter 2 that two’s-complement arithmetic is commutative and associative, even when overflow occurs.

    Hence the compiler may apply this optimization strategy to the code

  • On the other hand, floating-point multiplication and addition are not associative. Thus, combine5 and combine6 could produce different results due to rounding or overflow.

    So compilers won’t do this kind of transformation.

    (In most real-life applications, however, such patterns are unlikely. Since most physical phenomena are continuous, numerical data tend to be reasonably smooth and well behaved)

    ( It is unlikely that multiplying the elements in strict order gives fundamentally better accuracy than does multiplying two groups independently and then multiplying those products together)

    The programmer should decide whether they should make the trade-off or not.

5.9.2 Reassociation Transformation

We now explore another way to break the sequential dependencies and thereby improve performance beyond the latency bound

1
2
3
acc = (acc OP data[i]) OP data[i+1];
↓
acc = acc OP (data[i] OP data[i+1]);

combine7 performance

You may wondering how such a subtle change can make performance improvement since it still need 2 arithmetic which cannot be run in parallel.

The data flow graph give a clear view

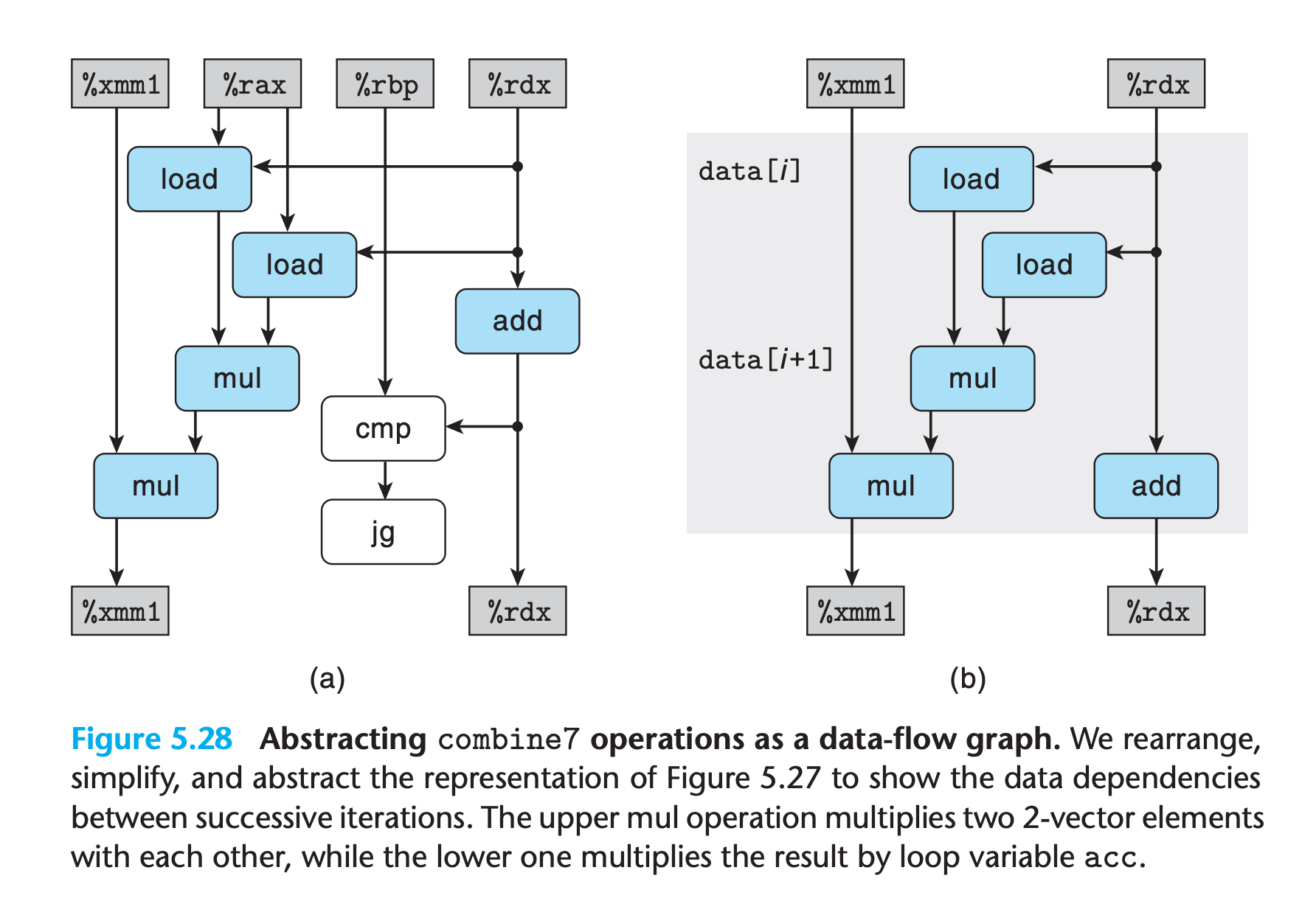
combine 7 graph

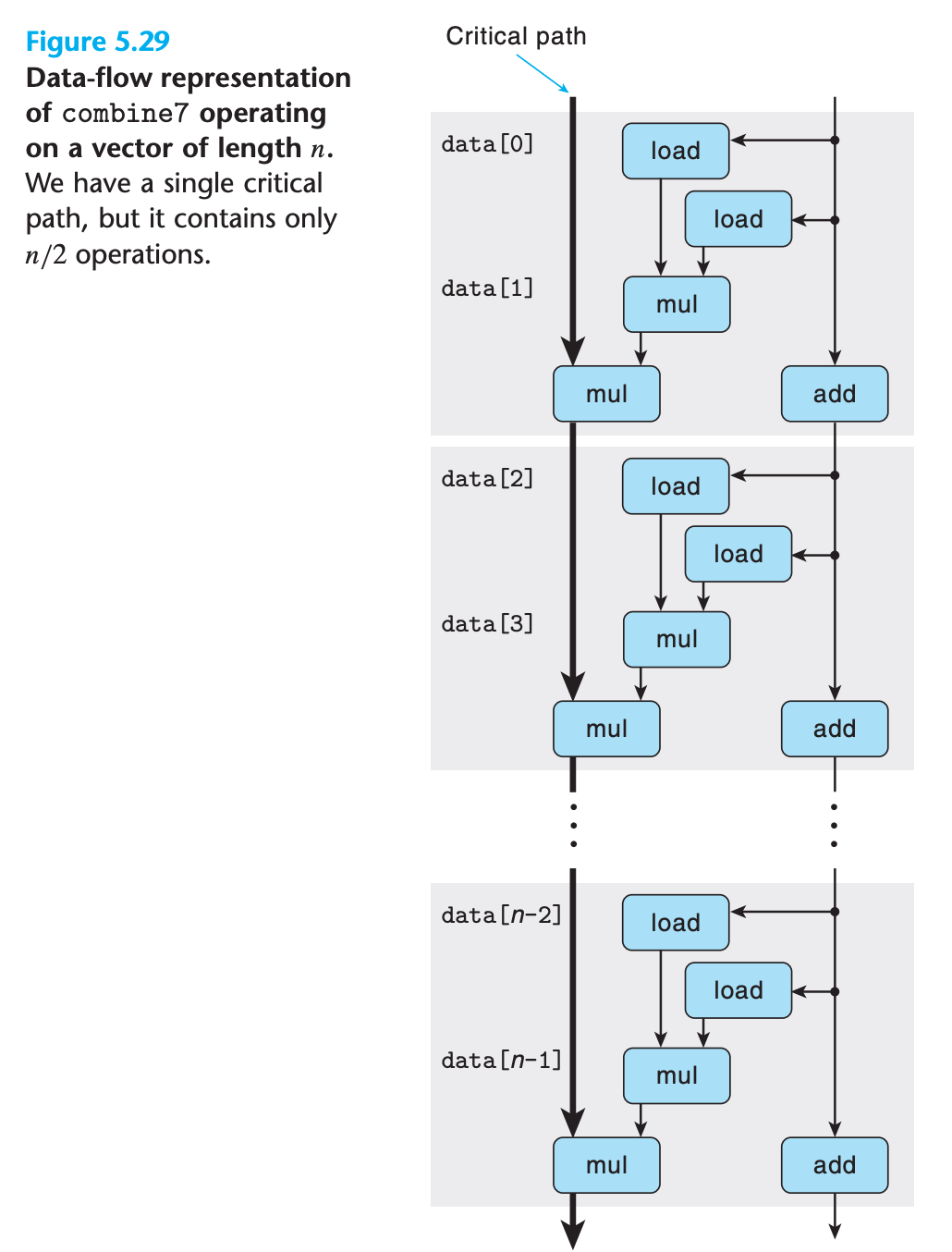
combine7 data flow

  • the operation data[i] OP data[i+1] do not need to wait for the previous iteration result, it can be done independently
  • As with the templates for combine5 and combine7, we have two load and two mul operations, but only one of the mul operations forms a data-dependency chain between loop registers
  • we only have n/2 operations along the critical path.

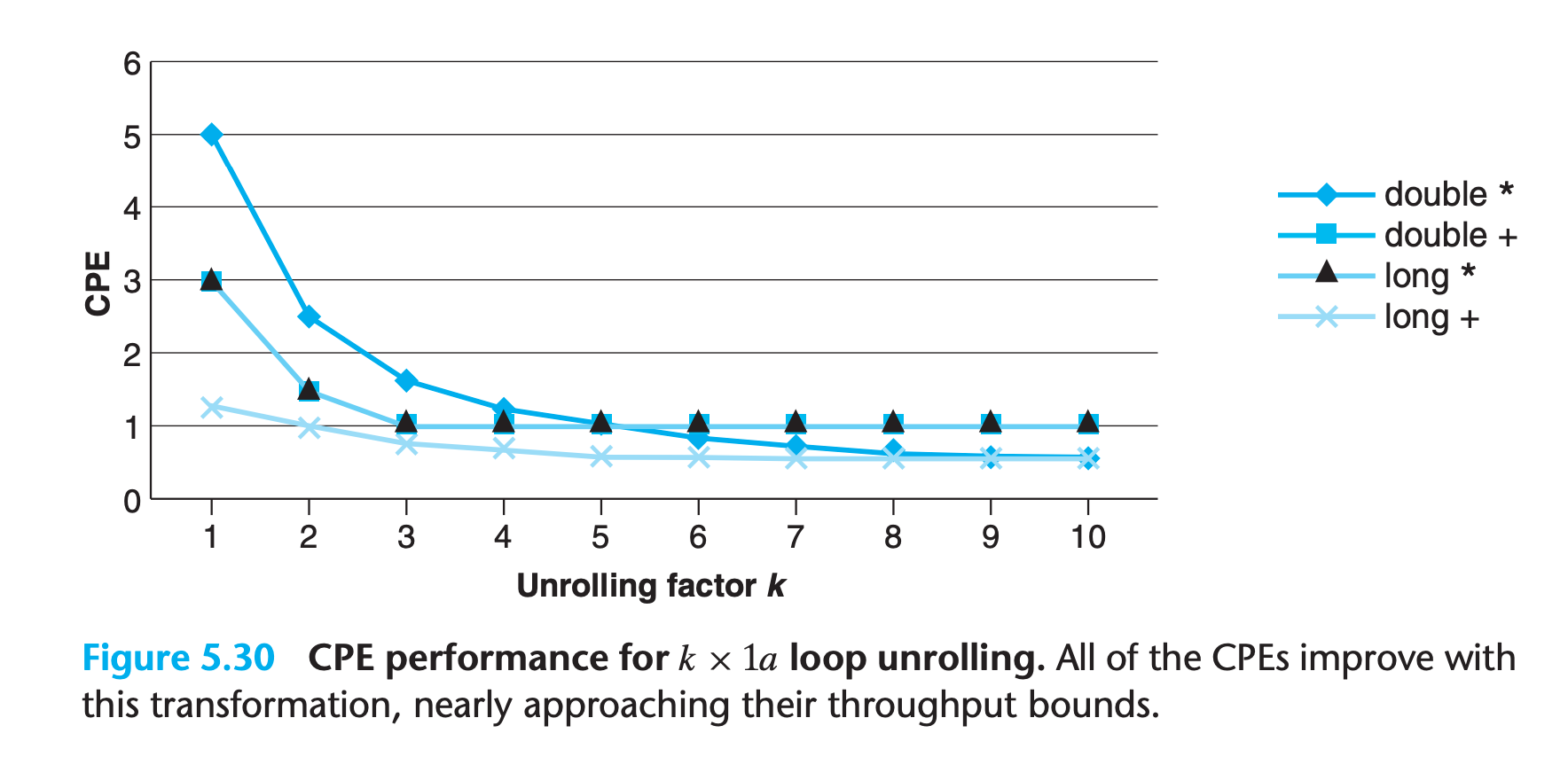
combine7 CPE

We can see that this transformation yields performance results similar to what is achieved by maintaining k separate accumulators with k × k unrolling

In performing the reassociation transformation, we once again change the order in which the vector elements will be combined together.

The assessment is just like the one in k × k unrolling.

Practice Problem 5.8

Consider the following function for computing the product of an array of n double precision numbers. We have unrolled the loop by a factor of 3.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
double aprod(double a[], long n)
{
long i;
double x, y, z;
double r = 1;
for (i = 0; i < n-2; i+= 3) {
x = a[i]; 
y = a[i+1];
z = a[i+2];
r = r * x * y * z; /* Product computation */
}
for (; i < n; i++)
r *= a[i];
return r;
}

For the line labeled “Product computation,” we can use parentheses to create five different associations of the computation, as follows:

1
2
3
4
5
r = ((r * x) * y) * z; /* A1 */
r = (r * (x * y)) * z; /* A2 */
r = r * ((x * y) * z); /* A3 */
r = r * (x * (y * z)); /* A4 */
r = (r * x) * (y * z); /* A5 */

Assume we run these functions on a machine where floating-point multiplication has a latency of 5 clock cycles. Determine the lower bound on the CPE set by the data dependencies of the multiplication. (Hint: It helps to draw a data-flow representation of how r is computed on every iteration.)

My solution : (:x: for A3 and A4)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/* A1 */
r*x;
(r*x)*y;
((r*x)*y)*z;
//5 + 5 + 5 = 15
/* A2 */
x0*y0       x1*y1     x2*y2       ...
(r*(x0*y0))
(r*(x0*y0))*z
           previous0*(x1*y1)
           previous0*(x1*y1)*z1
                        .....
//5 + 5 = 10
/* A3 and A4 */
x0*y0             x1*y1               x2*y2
(x0*y0)*z0        (x1*y1)*z1          (x2*y2)*z2
r*((x0*y0)*z0)
              previous0*(x1*y1)*z1
                               previous1*(x2*y2)*z2
                                                 .....
//critical path become the right side
//5 + 5 = 10
/* A5 */
r0*x0 y0*z0            y1*z1      y2*z2
    (r0*x0)*(y0*z0)
                 previous0*(x1)
                 previous0*x1*(y1*z1)
                               previous1*(x2)
                               previous1*(x2)*(y2*z2)
//5+5=10

Solution on the book :

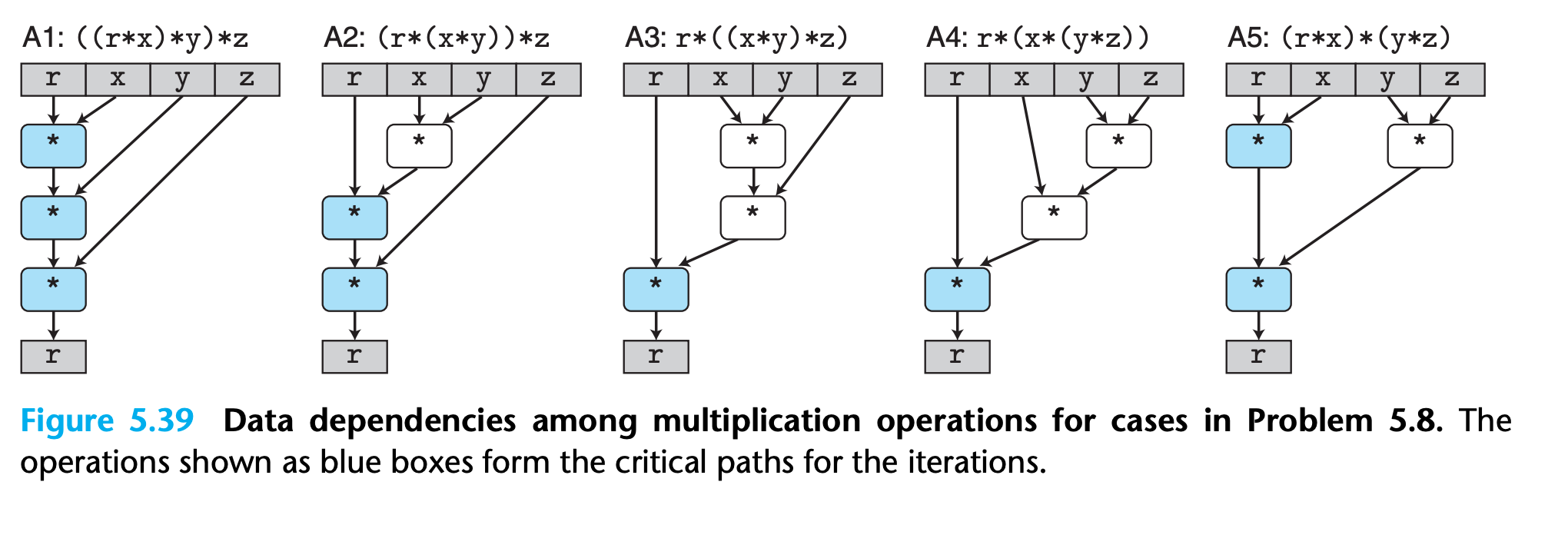
Solution

Note that only operation with a data dependency can form a critical path !!!

Hence the critical path of A3 and A4 is still the left side.

Intel introduced the SSE instructions in 1999, where SSE is the acronym for “streaming SIMD extensions”

The SSE capability has gone through multiple generations, with more recent versions being named advanced vector extensions, or AVX.

AVX instructions can perform vector operations on registers(%ymm0 ~ %ymm15), such as adding or multiplying eight or four sets of values in parallel

1
vmulps (%rcs), %ymm0, %ymm1

gcc supports extensions to the C language that let programmers express a program in terms of vector operations that can be compiled into the vector instructions of AVX

This coding style is preferable to writing code directly in assembly language.

This will also faciliate improve our performance.

Using a combination of gcc instructions, loop unrolling, and multiple accumulators, we are able to achieve the following performance for our combining functions

5.10 Summary of Results for Optimizing Combining Code

Our example demonstrates that modern processors have considerable amounts of computing power, but we may need to coax this power out of them by writing our programs in very stylized ways.

5.11 Some Limiting Factors

In this section, we will consider some other factors that limit the performance of programs on actual machines.

5.11.1 Register Spilling

If a program has a degree of parallelism P that exceeds the number of available registers, then the compiler will resort to spilling, storing some of the temporary values in memory, typically by allocating space on the run-time stack.

For example

1
2
3
4
5
6
7
8
9
#acc0 *= data[i]

#Updating of accumulator acc0 in 10 x 10 urolling
vmulsd (%rdx), %xmm0, %xmm0 

#Updating of accumulator acc0 in 20 x 20 unrolling
vmovsd 40(%rsp), %xmm0
vmulsd (%rdx), %xmm0, %xmm0
vmovsd %xmm0, 40(%rsp)

When register spilling happens the performance of our program may get worse rather than better.

5.11.2 Branch Prediction and Misprediction Penalties

A conditional branch can incur a significant misprediction penalty when the branch prediction logic does not correctly anticipate whether or not a branch will be taken

In a processor that employs speculative execution, the processor begins executing the instructions at the predicted branch target.

It does this in a way that avoids modifying any actual register or memory locations until the actual outcome has been determined.

  • If the predication is correct, the results will be “committed”
  • If the predication is wrong, the results will be discard

The misprediction penalty is incurred in doing this, because the instruction pipeline must be refilled before useful results are generated.

So how can we avoid this ?

There is no simple answer to this question, but the following general principles apply.

  • Do Not Be Overly Concerned about Predictable Branches

    • the branch prediction logic found in modern processors is very good at discerning regular patterns and long-term trends for the different branch instructions(with almost 90% accuracy)

  • Write Code Suitable for Implementation with Conditional Moves

    • This cannot be controlled directly by the C programmer, but some ways of expressing conditional behavior can be more directly translated into conditional moves than others.

    • We have found that gcc is able to generate conditional moves for code written in a more “functional” style, where we use conditional operations to compute values and then update the program state with these values(use ? : !!!), as opposed to a more “imperative” style, where we use conditionals to selectively update program state.

    • For example

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      /* Rearrange two vectors so that for each i, b[i] >= a[i] */
      void minmax1(long a[], long b[], long n) {
      long i;
      for (i = 0; i < n; i++) {
      if (a[i] > b[i]) {
      long t = a[i];
      a[i] = b[i];
      b[i] = t;
      }
       }
       }

      /* Rearrange two vectors so that for each i, b[i] >= a[i] */
      void minmax2(long a[], long b[], long n) {
      long i;
      for (i = 0; i < n; i++) {
      long min = a[i] < b[i] ? a[i] : b[i];
      long max = a[i] < b[i] ? b[i] : a[i];
      a[i] = min;
      b[i] = max;
      }
      }

    • Examing the assembly code or even embed assembly code directly is always the most realiable way.

5.12 Understanding Memory Performance

All modern processors contain one or more cache memories to provide fast access to small amounts of memory

5.12.1 Load Performance

In most of the cases, memory won’t be a bottleneck, whereas sometimes data dependency happens in loading will be a optimization blocker.

For example count the length of a linked list

1
2
3
4
5
6
7
8
9
10
11
12
typedef struct node {
    data_t data;
    struct node * next;
}Node;
int list_len(Node * ls){
    int cot = 0;
    while(ls){
        cot++;
        ls = ls->next;
    }
    return cot;
}
1
2
3
4
5
.L3
	addl $1,%rax;
	movq (%rdi),%rdi;  # the next pointer is depend on the previous one loaded from memory
	testq %rdi,%rdi;
	jne .L3

5.12.2 Store Performance

A series of store operations cannot create a data dependency since they don’t change register value in their very nature

Only a load operation is affected by the result of a store operation, since only a load can read back the memory value that has been written by the store.

For example

1
2
3
4
5
6
7
/* Set elements of array to 0 */
 void clear_array(long *dest, long n) {
 long i;
 for (i = 0; i < n; i++)
 dest[i] = 0;
}
//achieve best performance since not store operation need to wait

However combine load and store together we can have complex dependency

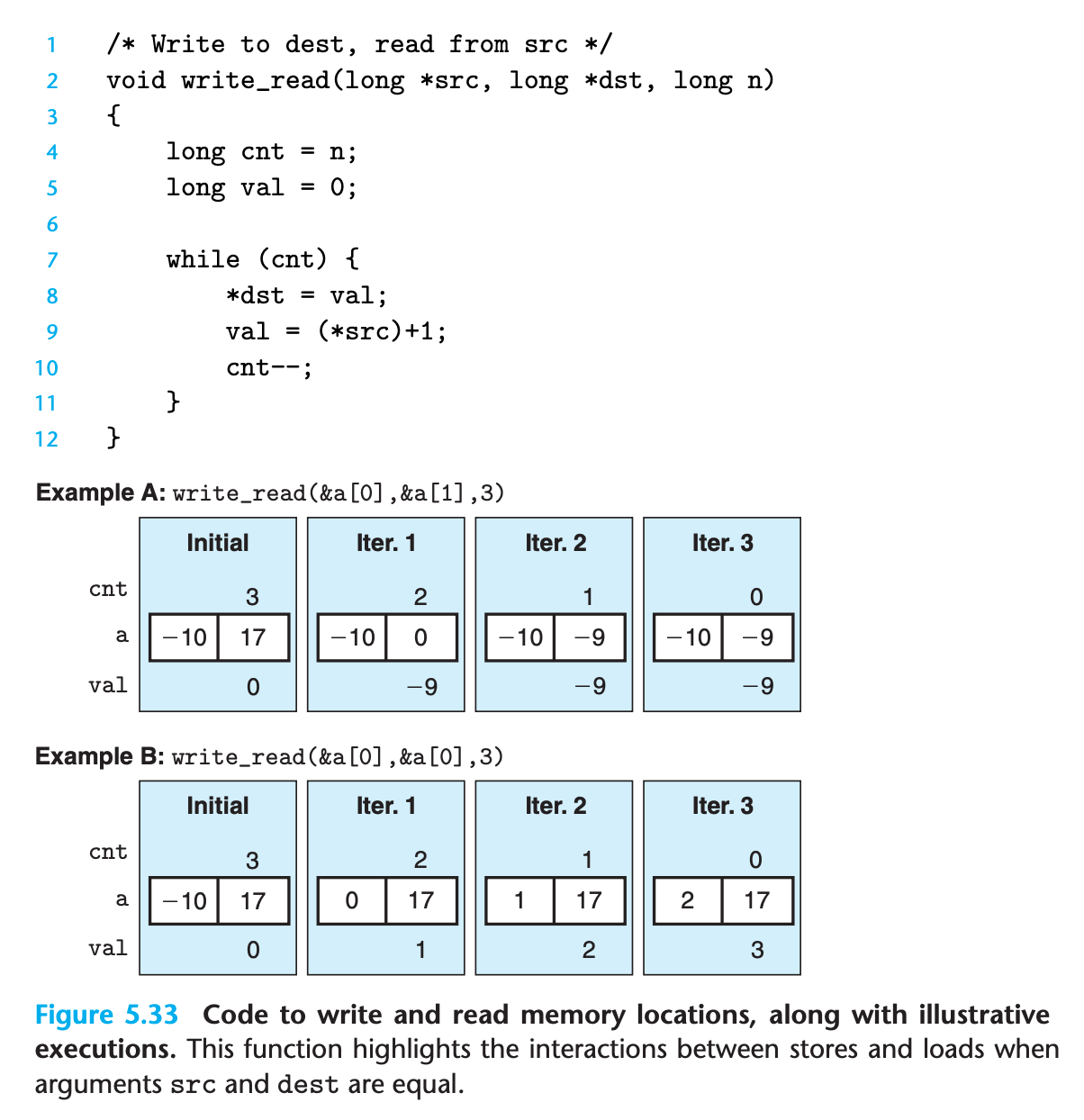
load and store

  • Measuring example A over a larger number of iterations gives a CPE of 1.3 since the read operation is not affected by write operation
  • Example B has a CPE of 7.3, the write/read dependency causes a slowdown in the processing of around 6 clock cycles.(it must wait for data to be written into the memory and then read it out)

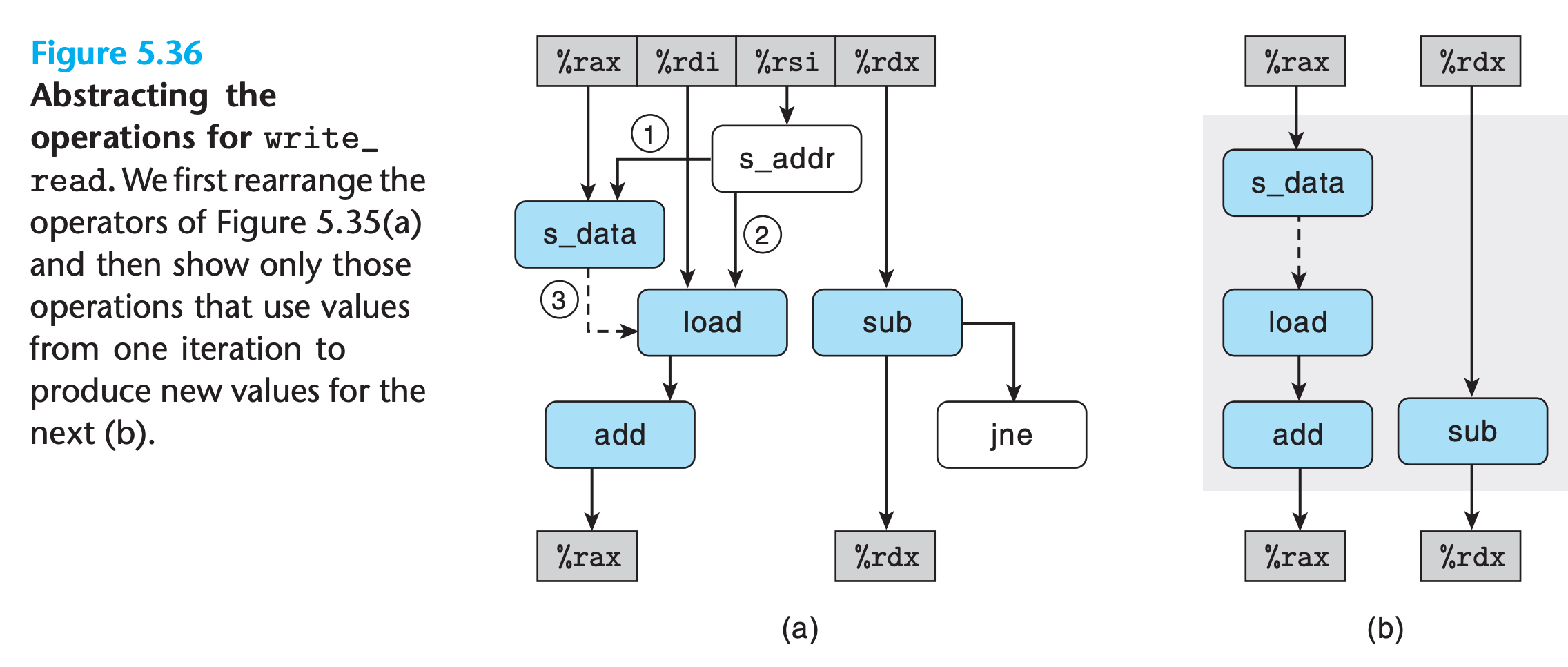
write and read graph

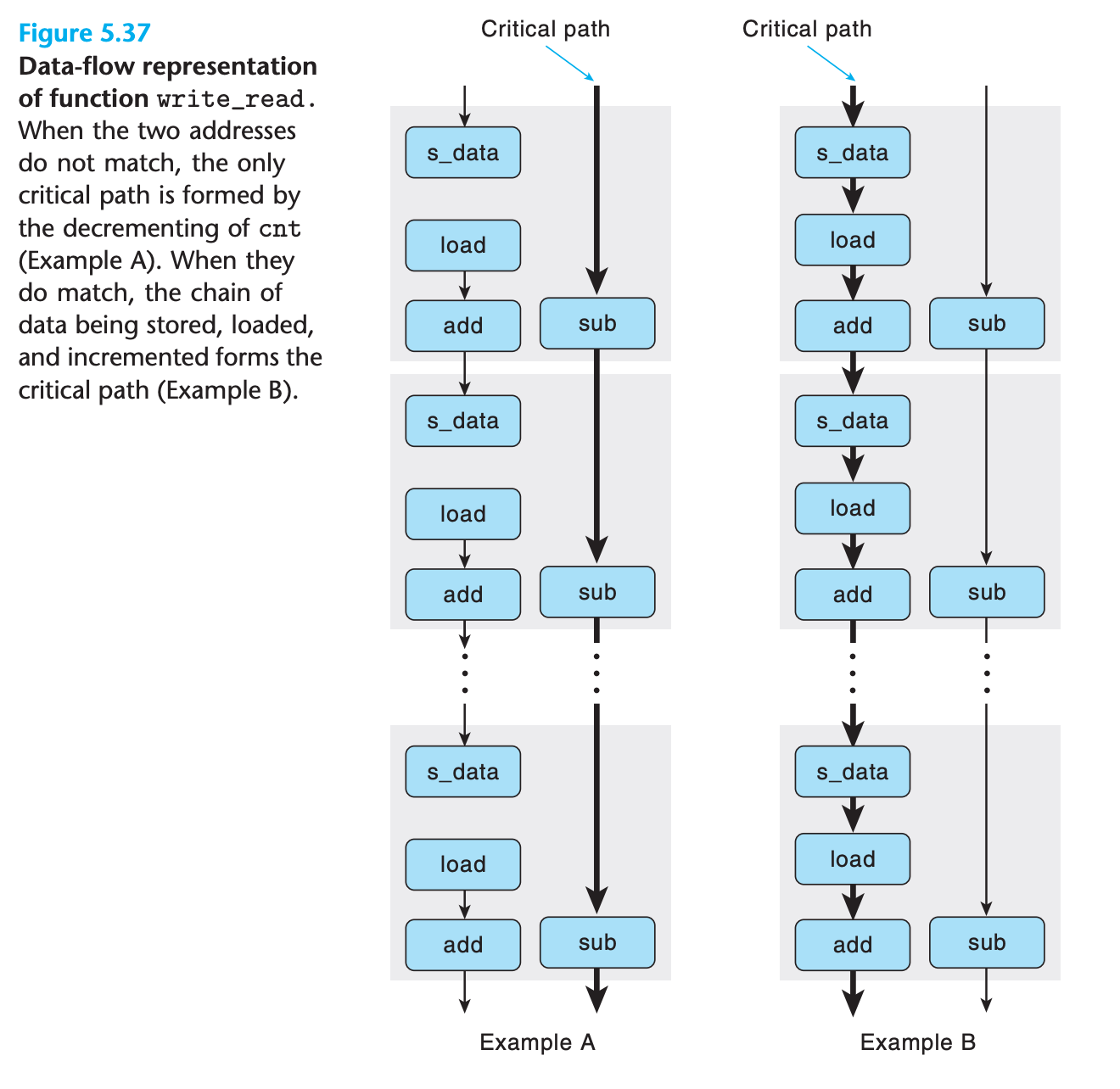
data flow

Practice Problem 5.10

As another example of code with potential load-store interactions, consider the following function to copy the contents of one array to another:

1
2
3
4
5
6
void copy_array(long *src, long *dest, long n)
{
 long i;
 for (i = 0; i < n; i++)
 dest[i] = src[i];
}

Suppose a is an array of length 1,000 initialized so that each element a[i] equals i.

A. What would be the effect of the call copy_array(a+1,a,999)?

B. What would be the effect of the call copy_array(a,a+1,999)?

C. Our performance measurements indicate that the call of part A has a CPE of 1.2 (which drops to 1.0 when the loop is unrolled by a factor of 4), while the call of part B has a CPE of 5.0. To what factor do you attribute this performance difference?

D. What performance would you expect for the call copy_array(a,a,999)?

My solution : :white_check_mark:

A: move a[1~999] to a[0~998]

B: move a[0~998] to a[1~999]

C: because A doesn’t form data dependency, the value to be read is not connected with the previous operation while B is exactly the opposite

D: same performance with A

5.13 Life in the Real World: Performance Improvement Techniques

We have described a number of basic strategies for optimizing program performance

  • High-level design
    • Choose appropriate algorithms and data structures for the problem at hand
  • Basic coding principles(use local variables)
    • Eliminate excessive function calls
    • Eliminate unnecessary memory references
  • Low-level optimizations
    • Unroll loops to reduce overhead and to enable further optimizations.
    • Find ways to increase instruction-level parallelism by techniques such as multiple accumulators and reassociation
    • Rewrite conditional operations in a functional style to enable compilation via conditional data transfers.(use cmov)

It is very easy to make mistakes when introducing new variables, changing loop bounds, and making the code more complex overall, please test them extensively!

5.14 Identifying and Eliminating Performance Bottlenecks

When working with large programs, even knowing where to focus our optimization efforts can be difficult.

5.14.1 Program Profiling

Program profiling involves running a version of a program in which instrumentation code has been incorporated to determine how much time the different parts of the program require

Unix systems provide the profiling program gprof

  • It determines how much CPU time was spent for each of the functions in the program
  • It computes a count of how many times each function gets called, categorized by which function performs the call.
Steps to use gprof
  1. The program must be compiled and linked for profiling. 
1
2
$ gcc -Og -pg prog.c -o prog
# -Og here to ensure gcc doesn't optimize function call into inline code
  1. Run the program as usual
1
$ ./prog

It will generate a gmon.out file

  1. gprof is invoked to analyze the data
1
$ gprof prog
Some properties of gprof are worth noting
  • The timing is not very precise due to OS interruption mechanism
  • . The calling information is quite reliable, assuming no inline substitutions have been performed.
  • By default, the timings for library functions are not shown