misc

markovChain

I happened to run into the Google foobar invitation when browsing the web. It is the doomsday-fuel problem led me here.

This artical is just note for patrickJMT markov Chain videos

Introduction example

Say we have two company sell a same kind of product. A shares 20% of the market, B shares 80% of the market.

A decide to launch an advertising campaign which will make

  • Those who use A, 90% will still use A
  • Those who use B, 70% will start to use A

This change will happen once a week as the campaign goes on.

Transition Graph

trans graph

Probability Matrix and State Matrix

1
2
3
4
5
6
7
8
9
10
11
12
13
>>> import numpy as np
>>> S0 = np.array([0.2 , 0.8]) # S0 is the initial state, denoting the market sharing
#  A    B
# [0.2 0.8]
>>> P = np.array( [ [0.9,0.1], [0.7,0.3] ])
# P is the probability matrix, indicating the transition
'''
	A      B
A  [0.9    0.1]
B  [0.7    0.3]
column stand for current state
row stand for next state
'''

Obtain the next state

Intuitive method

intuitive
$$
A=(0.2 \times 0.9)+(0.8 \times 0.7) = 0.74
$$

$$
B = (0.8 \times 0.3) + (0.2 \times 0.1) = 0.26
$$

Matrix Calculation

1
2
3
>>> S1 = np.matmul(S0,P)
>>> S1
array([0.74, 0.26])
1
2
3
>>> S2 = np.matmul(S1,P)
>>> S2
array([0.848, 0.152])
1
2
3
>>> S3 = np.matmul(S2,P)
>>> S3
array([0.8696, 0.1304])

==If the campaign goes on, will A’s market share converge???==

1
2
3
4
5
>>> for i in range(20):
...     S0 = np.matmul(S0,P)
...
>>> S0
array([0.875, 0.125])

It converges.
$$
0.875 \times 0.9 + 0.125 \times 0.7 = 0.875
$$

$$
0.875\times 0.1 + 0.125\times 0.7 = 0.125
$$

We call this final S matrix a stationary matrix and the final state a steady state of the system.

Question

  • Does every markov Chain has a unique stationary matrix ?
  • If a markov Chain has a stationary matrix will the successive matrix always approach it ?

Both answer is NO! Only a regular markov chain has these properties

Regular markov Chain

A transition matrix P is regular if some power of P has only positive entries.(NO zeros) A Markov chain is a regular Markov chain if its transition matrix is regular.

Find the stationary matrix

We only need to solve the equation below for any given P
$$
S \times P = S
$$

It alwasy converge

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
>>> S0
array([0.9, 0.1])
>>> _
array([0.9, 0.1])
>>> np.matmul(_,P)
array([0.88, 0.12])
>>> np.matmul(_,P)
array([0.876, 0.124])
>>> np.matmul(_,P)
array([0.8752, 0.1248])
>>> np.matmul(_,P)
array([0.87504, 0.12496])
>>> np.matmul(_,P)
array([0.875008, 0.124992])
>>> np.matmul(_,P)
array([0.8750016, 0.1249984])
>>> np.matmul(_,P)
array([0.87500032, 0.12499968])
>>> np.matmul(_,P)
array([0.87500006, 0.12499994])
>>> np.matmul(_,P)
array([0.87500001, 0.12499999])
>>> np.matmul(_,P)
array([0.875, 0.125])

Abosrbing Markov Chain

An abosorbing state is a state where has no way to leave that state.

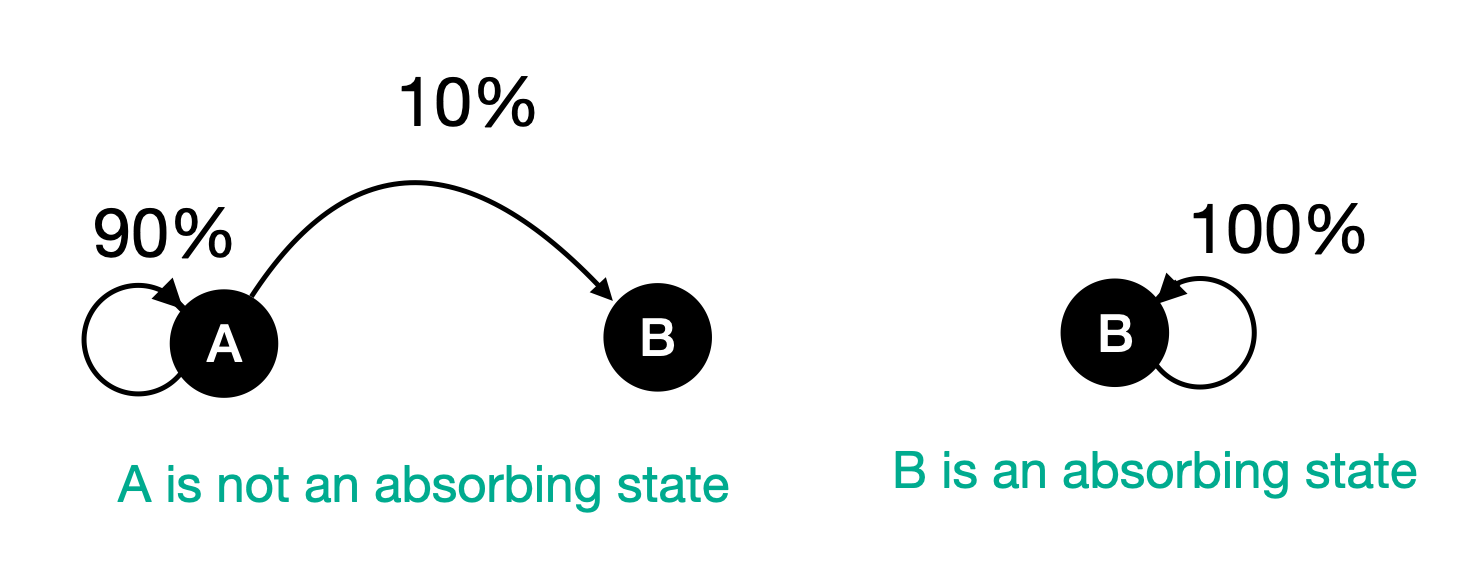
examples

We can easily determine if a matrix has absorbing state if we have labels in order.

1
2
3
4
5
6
7
"""
  A B C
A[x x x]
B[x x x]
C[x x x]
"""
# if we have any 1 in the diagonal, that state is an abosrbing state

Definition

A Markov chain is an absorbing chain if:

A) there is at least one absorbing state.

B) It is possible to go from each non-absorbing state to at least one absorbing state in a finite number of steps.

Standard form of absorbing Markov Chain

In a transition matrix, if all the absorbing states precede all the nonabsorbing states, the matrix is said to be in standard form. Standard forms are very useful in determining limiting matrices for absorbing Markov chains.

A standard form transition matrix can be partitioned into 4 submatrix
$$
P = \begin{bmatrix} I & 0\
R&Q
\end{bmatrix}
$$
I is an identity matrix and O is the zero matrix

Limiting Matrix

powers of P approach a limiting matrix P* where each row of P* is equal to the stationary matrix S if S exists

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
>>> np.matmul(P,P)
array([[0.88, 0.12],
       [0.84, 0.16]])
>>> np.matmul(_,P)
array([[0.876, 0.124],
       [0.868, 0.132]])
>>> np.matmul(_,P)
array([[0.8752, 0.1248],
       [0.8736, 0.1264]])
>>> np.matmul(_,P)
array([[0.87504, 0.12496],
       [0.87472, 0.12528]])
>>> np.matmul(_,P)
array([[0.875008, 0.124992],
       [0.874944, 0.125056]])
>>> np.matmul(_,P)
array([[0.8750016, 0.1249984],
       [0.8749888, 0.1250112]])
>>> np.matmul(_,P)
array([[0.87500032, 0.12499968],
       [0.87499776, 0.12500224]])
>>> np.matmul(_,P)
array([[0.87500006, 0.12499994],
       [0.87499955, 0.12500045]])
>>> np.matmul(_,P)
array([[0.87500001, 0.12499999],
       [0.87499991, 0.12500009]])
>>> np.matmul(_,P)
array([[0.875     , 0.125     ],
       [0.87499998, 0.12500002]])
>>> np.matmul(_,P)
array([[0.875, 0.125],
       [0.875, 0.125]])

We have a formula for P*
$$
P* = \begin{bmatrix}
I & 0\
FR&0
\end{bmatrix}, F = (I-Q)^{-1}
$$
$F$ is called the fundamental matrix for $P$

Properties of P*

  • P*[i][j] gives the long-run probability from state i to state j
  • sum of that row in $F$ is the average number of trials it will take to go from that non-absorbing state to a arbitrary absorbing state

The problem

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Doomsday Fuel
=============

Making fuel for the LAMBCHOP's reactor core is a tricky process because of the exotic matter involved. It starts as raw ore, then during processing, begins randomly changing between forms, eventually reaching a stable form. There may be multiple stable forms that a sample could ultimately reach, not all of which are useful as fuel. 

Commander Lambda has tasked you to help the scientists increase fuel creation efficiency by predicting the end state of a given ore sample. You have carefully studied the different structures that the ore can take and which transitions it undergoes. It appears that, while random, the probability of each structure transforming is fixed. That is, each time the ore is in 1 state, it has the same probabilities of entering the next state (which might be the same state).  You have recorded the observed transitions in a matrix. The others in the lab have hypothesized more exotic forms that the ore can become, but you haven't seen all of them.

Write a function solution(m) that takes an array of array of nonnegative ints representing how many times that state has gone to the next state and return an array of ints for each terminal state giving the exact probabilities of each terminal state, represented as the numerator for each state, then the denominator for all of them at the end and in simplest form. The matrix is at most 10 by 10. It is guaranteed that no matter which state the ore is in, there is a path from that state to a terminal state. That is, the processing will always eventually end in a stable state. The ore starts in state 0. The denominator will fit within a signed 32-bit integer during the calculation, as long as the fraction is simplified regularly. 

For example, consider the matrix m:
[
  [0,1,0,0,0,1],  # s0, the initial state, goes to s1 and s5 with equal probability
  [4,0,0,3,2,0],  # s1 can become s0, s3, or s4, but with different probabilities
  [0,0,0,0,0,0],  # s2 is terminal, and unreachable (never observed in practice)
  [0,0,0,0,0,0],  # s3 is terminal
  [0,0,0,0,0,0],  # s4 is terminal
  [0,0,0,0,0,0],  # s5 is terminal
]
So, we can consider different paths to terminal states, such as:
s0 -> s1 -> s3
s0 -> s1 -> s0 -> s1 -> s0 -> s1 -> s4
s0 -> s1 -> s0 -> s5
Tracing the probabilities of each, we find that
s2 has probability 0
s3 has probability 3/14
s4 has probability 1/7
s5 has probability 9/14
So, putting that together, and making a common denominator, gives an answer in the form of
[s2.numerator, s3.numerator, s4.numerator, s5.numerator, denominator] which is
[0, 3, 2, 9, 14].
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
from fractions import gcd
def lcm(a):
    lcm = 1
    for i in a:
        lcm = lcm*i//gcd(lcm, i)
    return lcm

class Fraction():
    def __init__(self , n, d):
        self.numerator =  n
        self.denominator = d

    def __add__(self , other):
        d , n = self.denominator * other.denominator , (self.numerator * other.denominator) + (other.numerator * self.denominator)
        return Fraction(n,d).reduced()

    def __sub__(self, other):
        other.numerator = - other.numerator
        return self + other

    def __mul__(self, other):
        return Fraction( self.numerator * other.numerator, self.denominator * other.denominator ).reduced()

    def reduced(self):
        divisor = gcd(self.numerator , self.denominator)
        if divisor == 0:
            return Fraction(0,1)
        else:
            return Fraction ( self.numerator // divisor,self.denominator // divisor )

    def __str__(self):
        return str(self.numerator)+ '/' + str(self.denominator)

    def __repr__(self):
        return self.__str__()

    def __float__(self):
        return float(self.numerator/self.denominator)

    def flipped(self):
        if self.numerator != 0:
            return Fraction(self.denominator , self.numerator)
        else:
            return self

    def __div__(self , other ):
        return  self * other.flipped()

    def getNumeratorOfdenominator(self , d):
        try:
            times = d // self.denominator
            return self.numerator * times 
        except:
            raise Exception("Unable")


# ======================================================= tool kit ======================================================= 
def transposeMatrix(m):
    return map(list,zip(*m))

def getMatrixMinor(m,i,j):
    return [row[:j] + row[j+1:] for row in (m[:i]+m[i+1:])]

def getMatrixDeternminant(m):
    #base case for 2x2 matrix
    if len(m) == 2:
        return m[0][0]*m[1][1]-m[0][1]*m[1][0]

    determinant = Fraction(0,1)
    for c in range(len(m)):
        determinant += Fraction((-1)**c,1) *m[0][c]*getMatrixDeternminant(getMatrixMinor(m,0,c))
    return determinant

def getMatrixInverse(m):
    determinant = getMatrixDeternminant(m)
    #special case for 2x2 matrix:
    if len(m) == 2:
        return [[m[1][1]/determinant, Fraction(-1,1)*m[0][1]/determinant],
                [Fraction(-1,1)*m[1][0]/determinant, m[0][0]/determinant]]

    #find matrix of cofactors
    cofactors = []
    for r in range(len(m)):
        cofactorRow = []
        for c in range(len(m)):
            minor = getMatrixMinor(m,r,c)
            cofactorRow.append( Fraction( ((-1)**(r+c)) , 1) * getMatrixDeternminant(minor))
        cofactors.append(cofactorRow)
    cofactors = transposeMatrix(cofactors)
    for r in range(len(cofactors)):
        for c in range(len(cofactors)):
            cofactors[r][c] = cofactors[r][c]/determinant
    return cofactors


def MM(a,b):
    c = []
    for i in range(0,len(a)):
        temp=[]
        for j in range(0,len(b[0])):
            s = Fraction(0,1)
            for k in range(0,len(a[0])):
                s += a[i][k]*b[k][j]
            temp.append(s)
        c.append(temp)
    return c


# ======================================================= tool kit ======================================================= 



def rearrange(info):
    absorb = []
    nonabs = []
    for name , v in info.items():
        if v[1] :
            absorb.append((name , v[0]))
        else:
            nonabs.append((name , v[0]))
    absorb = sorted(absorb , key=lambda x : x[0])
    nonabs = sorted(nonabs , key=lambda x : x[0])
    ls = absorb + nonabs
    names = [x[0] for x in ls]
    P = [] # Probability Matrix
    for i in ls:
        row = []
        paths = i[1]
        ks = sorted(paths , key=lambda x : names.index(x))
        for k in ks:
            row.append(paths[k])
        P.append(row)
    return P,len(absorb)

        
def showinfo(m):
    for k , v in m.items():
        print(k, ":", "abosrbing ? " , v[1])
        for x,y in v[0].items():
            print("\t" , x, "->" , y)


def getinfo(m):
    res  = {}
    for index, row in enumerate(m):
        name = "S" + str(index)
        paths = {}
        denominator = sum(row)
        for i , n in enumerate(row):
            path = "S" + str(i)
            if denominator != 0:
                paths[path] = Fraction(n , denominator)
            else:
                # absorbing state
                if index == i:
                    paths[path] = Fraction(1, 1)
                else:
                    paths[path] = Fraction(0 , 1)
        res[name] = ( paths , denominator == 0 )
    return res


def submatrix(P , indice):
    R = []
    Q = []
    for row in P[indice:]:
        R.append(row[:indice])
        Q.append(row[indice:])
    return R,Q


def Fundamental(Q):
    length  = len(Q)
    I = [[Fraction(1,1) if r==i else Fraction(0,1) for i in range(length)] for r in range(length)]
    Finv = []
    for Ir , Qr in zip(I,Q):
        row = [i-q for i,q in zip(Ir ,Qr)]
        Finv.append(row)
    F = getMatrixInverse(Finv)
    return F





# =================== MAIN ====================


def solution(m):
    if len(m) == 1 and len(m[0]) == 1 and m[0][0] == 0 : return [1,1]
    info = getinfo(m)
    P , indice = rearrange(info)
    R , Q = submatrix(P , indice)
    F = Fundamental(Q)
    res = MM(F,R)[0]
    denominator = lcm([f.denominator for f in res])
    ans =  [f.getNumeratorOfdenominator(denominator) for f in res] + [denominator]
    return ans
  • A view from linear algebra perspective is also heuristic MIT 18.06 (using the Eigen values and Eigen vectors)