Introduction

MIT 18.06

MIT 18.06

L1 : The geometry of linear algebra

The fundamental of linear algebra is to represent the linear equation system

Three big picture

• Row picture
• Column picture
• Matrix picture

Example

$$
\begin{cases}
2x-y=0\
-x+2y=3
\end{cases}
$$

Can be represented in the form of matrix

$$
\begin{bmatrix}
2 & -1 \
-1 & 2
\end{bmatrix}
\begin{bmatrix}
x\
y
\end{bmatrix}
=
\begin{bmatrix}
0\
3
\end{bmatrix}
$$

$$
AX=B
$$

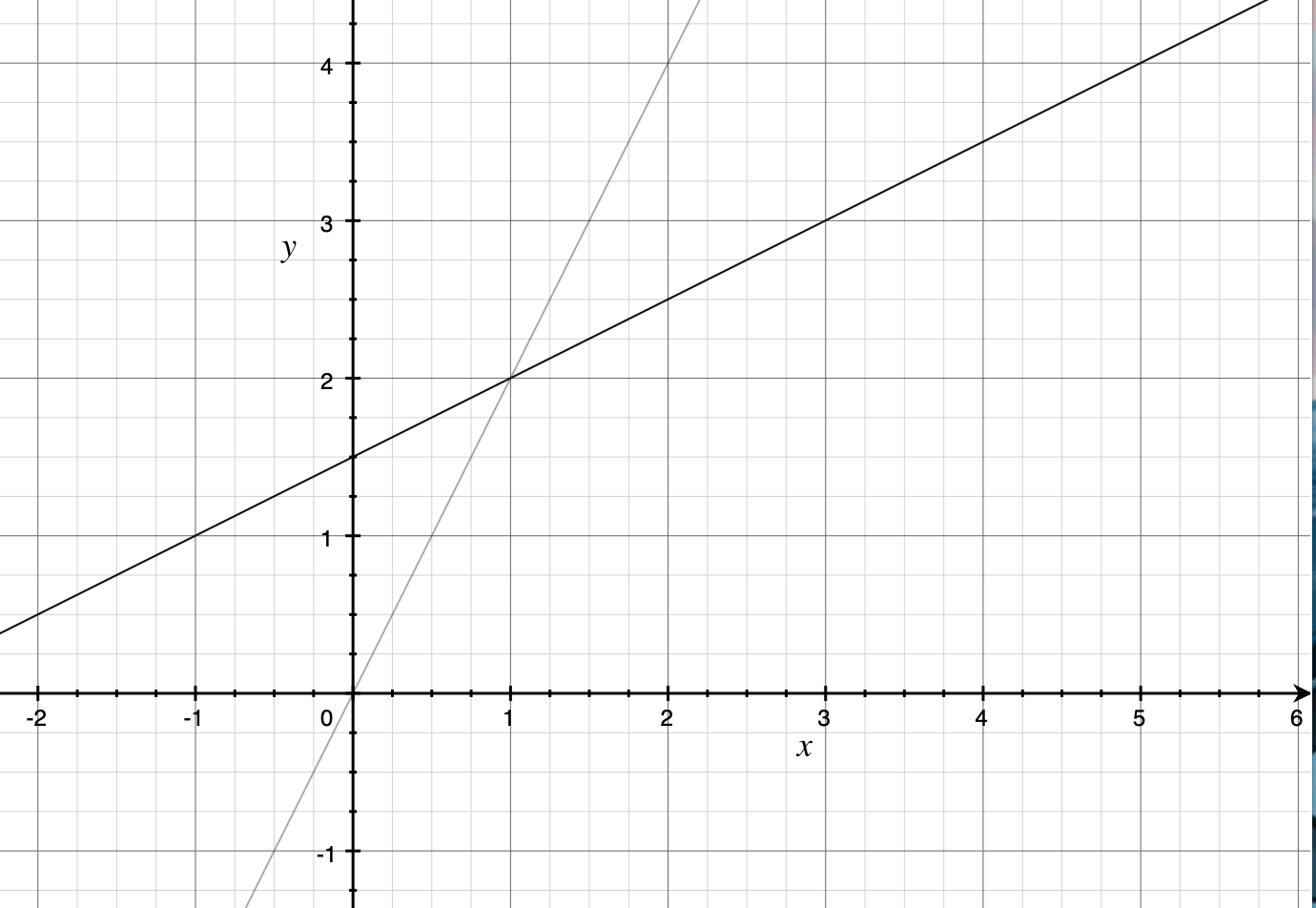
Row picture

view the equations in order of row

• $2x-y=0$ gives a line composed with all points satisfy the equation
• $-x+2y=3$ does the same
• We can have the intersect point as the answer

Column picture

find linear combination of the coefficients

important perspective !

Linear combination !

$$
x\begin{bmatrix}
2 \ -1
\end{bmatrix}
+y\begin{bmatrix}
-1 \ 2
\end{bmatrix}
=
\begin{bmatrix}
0\3
\end{bmatrix}
$$

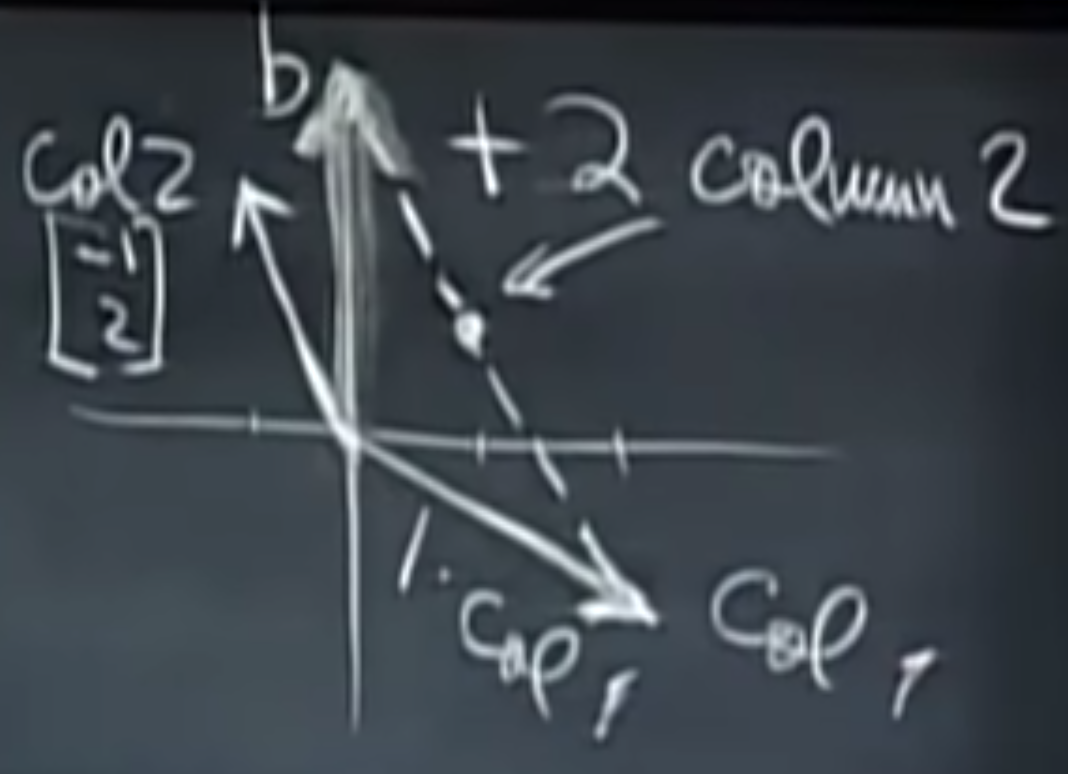
• The combination of vectors
• In fact, using the given two bases, we can get to any point in the 2-D space. We say that the two bases forms a space.
• However, not all bases can form a space, for example $2x+y = 0$ and $4x+2y=0$
  • Since $(2,4)$ and $(1,2)$ align in a same line, they can not go other direction. They have somewhat dependency
  • We have a dimension loss ! (result from dependency)
  • This is the same for 3D,4D,… (3 vectors align in the same plain, dimension loss!)

Matrix Multiplication

$$
\begin{bmatrix}
2 & 5 \
1 & 3
\end{bmatrix}
\begin{bmatrix}
1\2
\end{bmatrix}
$$

Column view (recommended !)

start from the right matrix and linear combination

$$
AX=B
$$

$X$ is a combination of $A$ which gives $B$

$$
1 \begin{bmatrix}
2 \ 1
\end{bmatrix}
+
2\begin{bmatrix}
5 \ 3
\end{bmatrix}
=\begin{bmatrix}
2+10 \ 1+6
\end{bmatrix}
=
\begin{bmatrix}
12 \ 7
\end{bmatrix}
$$

Row view

row by row

$$
\begin{bmatrix}
2 & 5 \
1 & 3
\end{bmatrix}
\begin{bmatrix}
1\2
\end{bmatrix} =
\begin{bmatrix}
2 + 10 \
1 + 6
\end{bmatrix}
$$

L2 : Elimination with matrixes

This is the method how computer solve equations

Matrix is a language

Elimination : success

The Gaussian elimination : Canceling the variables one by one

Example

The equations

$$
\begin{cases}
x + 2y + z = 2 \
3x + 8y+z = 12 \
4y + z = 2
\end{cases}
$$

The matrix

$$
\begin{bmatrix}
1 & 2 & 1\
3 & 8 & 1\
0 & 4 & 1
\end{bmatrix}
\begin{bmatrix}
x\ y \z
\end{bmatrix}
= \begin{bmatrix}
2\ 12 \2
\end{bmatrix}
$$

We just cancel out variables via normal math

Cancel pivot [0][0]

line2 = line2 - 3 * line1

$$
\begin{bmatrix}
1 & 2 & 1\
0 & 2 & -2\
0 & 4 & 1
\end{bmatrix}

= \begin{bmatrix}
2\ 6 \2
\end{bmatrix}
$$

Cancel pivot [1][1]

line3 -= 2*line2

$$
\begin{bmatrix}
1 & 2 & 1\
0 & 2 & -2\
0 & 0 & 5
\end{bmatrix}

= \begin{bmatrix}
2\ 6 \-10
\end{bmatrix}
$$

Elimination : failure

• We do not allow pivot to be $0$, so if it is, we just change the order of rows, that is to say, choose another equation to cancel with.
• Fatal failure : when canceling the pivot, the next pivot is also cancelled. In other word, the “actual” given equations do not provide enough constraints to solve the problem.

Back substitution

Just substitute the pivots with their value in backwards order

The equations after transformation

$$
\begin{cases}
x + 2y + z = 2\
2y-2z = 6 \
5z = -10
\end{cases}
$$

$$
\begin{cases}
x = 2\
y =1 \
z = -2
\end{cases}
$$

The Matrix Language

The operations performed on matrixes can also be expressed in form of matrixes!

Multiply by left : row selector

The result is a linear combination of rows

x # select row 1
y # select row 2
z # select row 3

$$
\begin{bmatrix}
x & y & z
\end{bmatrix}
\begin{bmatrix}
a_1 & b_1 & c_1\
a_2 & b_2 & c_2\
a_3 & b_3 & c_3
\end{bmatrix}

= \begin{bmatrix}
x’ & y’ & z’
\end{bmatrix}
$$

$$
\begin{cases}
x’ = a_1x+a_2y+a_3z\
y’ = b_1x+b_2y+b_3z\
z’ = c_1x + c_2y+c_3z
\end{cases}
$$

$$
\begin{bmatrix}
x’ & y’ & z’
\end{bmatrix}
=\begin{bmatrix}
a_1x& b_1x & c_1x
\end{bmatrix}+\begin{bmatrix}
a_1y& b_1y & c_1y
\end{bmatrix}+\begin{bmatrix}
a_1z& b_1z & c_1z
\end{bmatrix}
$$

$$
\begin{bmatrix}
x’ & y’ & z’
\end{bmatrix}
= x \begin{bmatrix}
a_1& b_1 & c_1
\end{bmatrix}+y\begin{bmatrix}
a_1& b_1 & c_1
\end{bmatrix}+z\begin{bmatrix}
a_1& b_1 & c_1
\end{bmatrix}
$$

Multiply by right : column selector

the linear combination

$$
\begin{bmatrix}
a_1 & b_1 & c_1\
a_2 & b_2 & c_2\
a_3 & b_3 & c_3
\end{bmatrix}
\begin{bmatrix}
x \ y \ z
\end{bmatrix}
= \begin{bmatrix}
x’ \ y’ \ z’
\end{bmatrix}
$$

$$
\begin{bmatrix}
x’ \ y’ \ z’
\end{bmatrix} = x\begin{bmatrix}
a_1 \ a_2 \ a_3
\end{bmatrix}
+y\begin{bmatrix}
b_1 \ b_2 \ b_3
\end{bmatrix}
+z\begin{bmatrix}
c_1 \ c_2 \ c_3
\end{bmatrix}
$$

Express the Elimination in Matrix language

line2 = line2 - 3 * line1

$$
\begin{bmatrix}
1 & 0 & 0\
-3 & 1 & 0\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
1 & 2 & 1\
3 & 8 & 1\
0 & 4 & 1
\end{bmatrix} = \begin{bmatrix}
1 & 2 & 1\
0 & 2 & -2\
0 & 4 & 1
\end{bmatrix}
$$

• Select 3 rows from the old matrix
• The first row will be 1*old_first_row + 0*old_second_row+0*old_third_row
• The second row will be -3*old_first_row + 1*old_second_row+0*old_third_row
• …
• And this is why the identity matrix is “identity”, it only select the original ones and do nothing

Associativity

$$
E_1(E_2A) = U
$$

$$
(E_1E_2)A = U
$$

---

Multiplication of Matrixes

Column View

$$
m \Biggl{ \underbrace{
\begin{bmatrix}
a_{11} & a_{12} & … &a_{1n}\
a_{21}&a_{22}&…&a_{2n}\
…&…&…&…\
a_{m1}&a_{m2}&…&a_{mn}
\end{bmatrix}
}n
\times
n \Biggl{ \underbrace{
\begin{bmatrix}
b{11} & b_{12} & … &b_{1p}\
b_{21}&b_{22}&…&a_{2p}\
…&…&…&…\
a_{n1}&a_{n2}&…&a_{np}
\end{bmatrix}
}_p
$$

$$
\stackrel{\text{concatenation of }}{=}

\begin{bmatrix}
a_{11} & a_{12} & … &a_{1n}\
a_{21}&a_{22}&…&a_{2n}\
…&…&…&…\
a_{m1}&a_{m2}&…&a_{mn}
\end{bmatrix}
\times
\begin{bmatrix}
b_{11}\
b_{21}\
…\
b_{n1}
\end{bmatrix}
$$

The result is concatenation of linear combination of matrix A, Columns of result are combination of columns of A

Since there are $n$ vectors in A, so B must have $n$ rows, $p$ can be whatever

Row View

$$
\stackrel{ \text{vertically concatenation}}{=}
\begin{bmatrix}
a_{11}&a_{12}&…&a_{1n}
\end{bmatrix}
\times
\begin{bmatrix}
b_{11} & b_{12} & … &b_{1p}\
b_{21}&b_{22}&…&a_{2p}\
…&…&…&…\
a_{n1}&a_{n2}&…&a_{np}
\end{bmatrix}

$$

Since there are $n$ rows in B, so A must have $n$ columns, $m$ can be whatever

Rows of result are combination of rows of B

The forth way

What if we do column * row instead of regular row * column ?

$$
m \Biggl{ \underbrace{
\begin{bmatrix}
a_{11} \
a_{21}\
…&\
a_{m1}
\end{bmatrix}
}1
\times
1 { \underbrace{
\begin{bmatrix}
b{11} & b_{12} & … &b_{1p}
\end{bmatrix}
}_p
$$

We get a full matrix !

$$
AB= \sum(\text{columns of A)} \times (\text{rows of B})
$$

Example

$$
\begin{bmatrix}
2 & 7 \
3 & 8 \
4 & 9
\end{bmatrix}
\times
\begin{bmatrix}
1&6\
0 & 0
\end{bmatrix}
$$

$$

\begin{bmatrix} 2 \ 3 \ 4 \end{bmatrix} \times \begin{bmatrix}1 & 6\end{bmatrix}
+\begin{bmatrix} 7 \ 8 \ 9 \end{bmatrix} \times \begin{bmatrix}0 & 0\end{bmatrix}

$$

$$

\begin{bmatrix}
2 & 12 \
3 & 18 \
4 & 24
\end{bmatrix}
+
\begin{bmatrix}
0 & 0 \
0 & 0 \
0 & 0
\end{bmatrix}
$$

>>> A = array( [ [2,7],[3,8],[4,9] ] )
>>> B = array( [ [1,6] , [0,0] ] )
>>> matmul(A,B)
array([[ 2, 12],
       [ 3, 18],
       [ 4, 24]])

Block View

We can split matrix into sub matrix and treat them as elements.

$$
AB = \left[
\begin{array}{c|c} A_{11} & A_{12} \\hline A_{21} & A_{22} \end{array} \right]\cdot
\left[
\begin{array}{c|c} B_{11} & B_{12} \\hline B_{21} & B_{22} \end{array} \right]
=
\left[
\begin{array}{c|c} A_{11}B_{11}+A_{12}B_{21} & A_{11}B_{12}+A_{12}B_{22} \\hline A_{21}B_{11}+A_{22}B_{21} & A_{22}B_{12}+A_{22}B_{22} \end{array} \right]
$$

Recollect the strategy for faster matrix multiplication by exploiting the cache

Inverse

only square is invertible

Singular/non-invertible matrix

$$
\text{You can find a non zero}\ \vec{x},\text{gives }A \vec{x} = 0
$$

$$
\because \text{if} \exist A ^{-1}
$$

$$
\therefore A^{-1}A=I
$$

$$
\therefore A^{-1}A \vec{x} = 0
$$

$$
\therefore \vec{x} = 0 , \text{confliction}
$$

$A$ transform $\vec{x}$ into $0$ and there is no way to get back $\vec{x}$, so $A$ is non-invertible

Gaussian Jorden Elimination

How can we find the inverse matrix ?

$$
A^{-1} \cdot [\begin{array}{c|c} A & I \end{array}] = [\begin{array}{c|c} I & A^{-1} \end{array}]
$$

So we only need to transform $A$ into $A^{-1}$ along with $I$

Example

$$
A= \begin{bmatrix} 1 & 3 \ 2 & 7 \end{bmatrix} , A^{-1}?
$$

First we come with Gaussian

$$
[A|I] =
\Big[\begin{array}{cc|cc}
1 & 3 & 1 & 0\
2 & 7 & 0 &1
\end{array}\Big]
$$

$$
\stackrel{\text{row2 += row1 * -2 }}{=}
\Big[\begin{array}{cc|cc}
1 & 3 & 1 & 0\
0 & 1 & -2 & 1
\end{array}\Big]
$$

Then Jorden say we cancel upwards

$$
\stackrel{\text{row1 += -3 * row2}}{=}
\Big[\begin{array}{cc|cc}
1 & 0 & 7 & -3\
0 & 1 & -2 & 1
\end{array}\Big]
$$

$$
A^{-1} = \begin{bmatrix} 7 & -3 \ -2 & 1 \end{bmatrix}
$$

More about the example

row2 += row1 * -2

$$
\begin{bmatrix}
1 & 0 \
-2 & 1
\end{bmatrix}
\cdot
\Big[\begin{array}{cc|cc}
1 & 3 & 1 & 0\
2 & 7 & 0 & 1
\end{array}\Big]
$$

$$

\Bigg[
\begin{array}{c|cc}
\begin{bmatrix}
1 & 0 \
-2 & 1
\end{bmatrix}
\begin{bmatrix}
1 & 3 \
2 & 7
\end{bmatrix}
&
\begin{bmatrix}
1 & 0 \
-2 & 1
\end{bmatrix}
\begin{bmatrix}
1 & 0 \
0 & 1
\end{bmatrix}
\end{array}

\Bigg]
$$

$$
= \Big[\begin{array}{cc|cc}
1 & 3 & 1 & 0\
0 & 1 & -2 & 1
\end{array}\Big]
$$

row1 += -3 * row2

$$
\begin{bmatrix}
1 & -3\
0 & 1
\end{bmatrix}
\cdot
\Big[\begin{array}{cc|cc}
1 & 3 & 1 & 0\
0 & 1 & -2 & 1
\end{array}\Big]
$$

$$
= \Big[\begin{array}{cc|cc}
1 & 0 & 7 & -3\
0 & 1 & -2 & 1
\end{array}\Big]
$$

$$
= \begin{bmatrix}
1 & -3\
0 & 1
\end{bmatrix}
\cdot
\begin{bmatrix}
1 & 0 \
-2 & 1
\end{bmatrix}
\cdot
\Big[\begin{array}{cc|cc}
1 & 3 & 1 & 0\
2 & 7 & 0 & 1
\end{array}\Big]
$$

So the inverse can also be obtained by

$$
\begin{bmatrix}
1 & -3\
0 & 1
\end{bmatrix}
\cdot
\begin{bmatrix}
1 & 0 \
-2 & 1
\end{bmatrix}
=
\begin{bmatrix}
7 & -3 \
-2 & 1
\end{bmatrix}
= A^{-1}
$$

Homework

problem set

• pset1
• pset2
• pset3
  skipped pset4
• pset5
• pset6
• pset7
• pset8
• pset9

psets on Github(Jupyter Notebook version)