Application of Linear Algebra in real world – Graph
Representation : Incidence Matrix
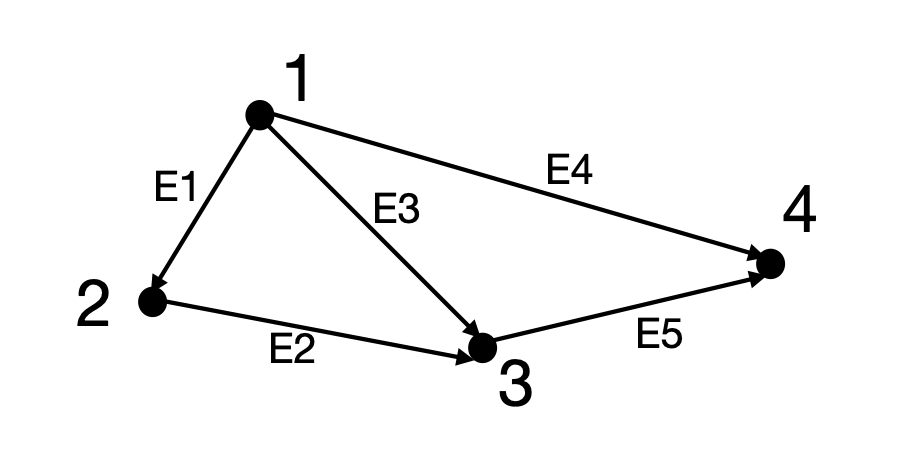
Row represent edges
Column represent nodes
Positive if the end point, negative if start point
$$
A = \begin{bmatrix}
-1 & 1 & 0 & 0\
0 & -1 & 1 & 0\
-1 & 0 & 1 & 0\
-1 & 0 & 0 & 1\
0 & 0 & -1 & 1
\end{bmatrix}
$$
Apply matrix methods to it
By reducing the matrix to echelon form, we can see the rank is 3
$$
R = \begin{bmatrix}
1 & 0 & 0 & -1\
0 & 1 & 0 & -1\
0 & 0 & 1 & -1\
0 & 0 & 0 & 0\
0 & 0 & 0 & 0
\end{bmatrix}
$$
$$
N(A) = \begin{bmatrix} -F \ I \end{bmatrix} = C\begin{bmatrix}
1\1 \1 \ 1
\end{bmatrix}
$$
$$
\begin{bmatrix}
1 & 0 & 0 & -1\
\end{bmatrix} \text{gives, } \text{node}_1 - \text{node}_2 = 0
$$
This gives us the [voltage, electronic potential differences](Voltage - Wikipedia)
If all voltages are equal $C=C=C$, no current will flow in the network
KCL
How about the rows ? Let’s see how $A^TY=0$
The equation gives Kirchhoff’s current law(KCL)
For each node, income current should equals outcome current, that is, the node do not hold any current.
The $N(A^T)$ will gives us for what edges we can satisfy the law.
Loop
since rows represent edges
linear dependent rows gives a loop
a graph without loops is a tree
For any graph, the rank(number of non-loop edge) is always number of nodes - 1
This gives the linear algebra prove of Euler’s formula
$$
Dim(N(A^T)) = m - r
$$
1 | len(loops) == len(edges) - (len(nodes) - 1) |