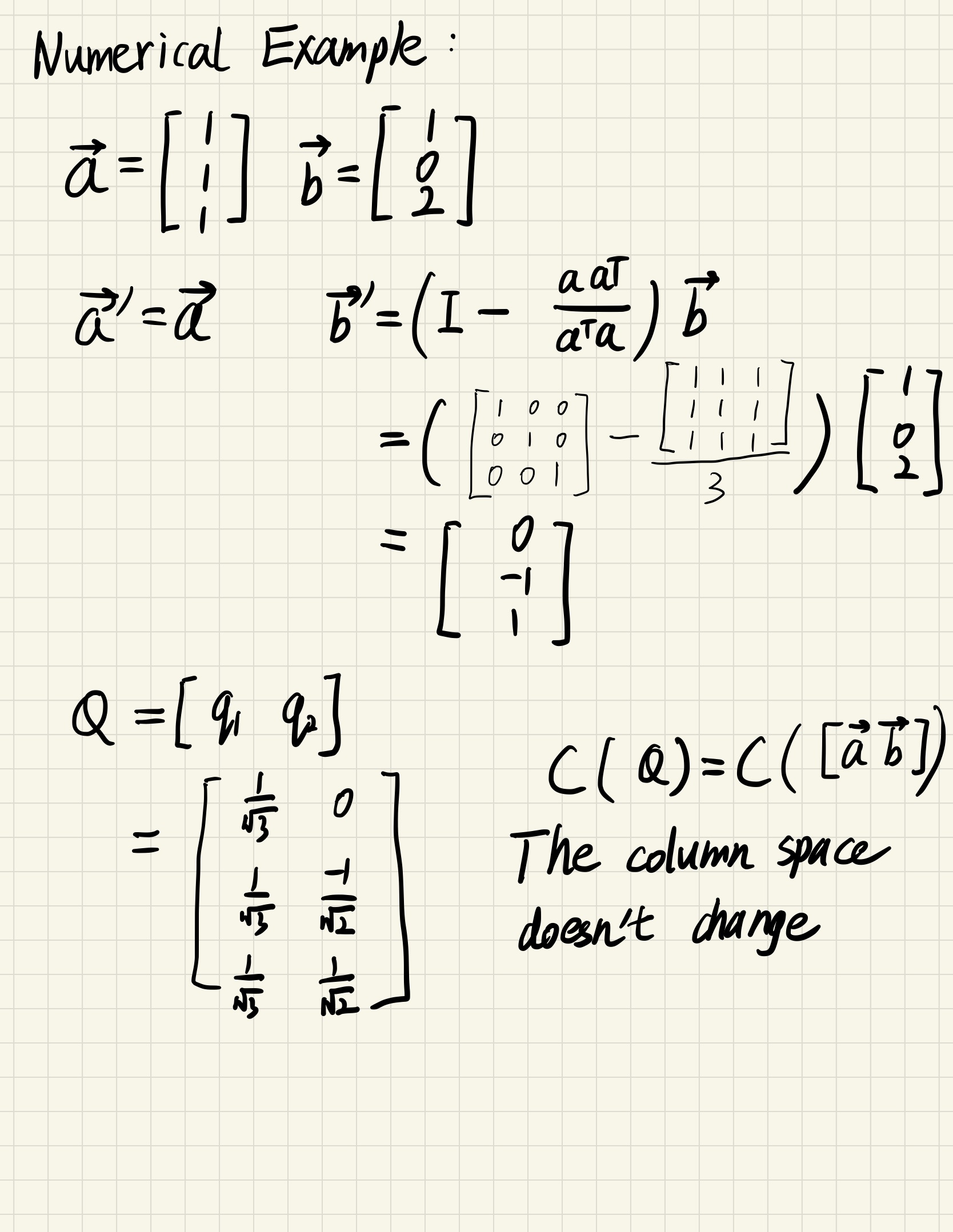Orthogonal : 正交
Orthogonal is just another word for perpendicular
We all know $\vec{x} \cdot \vec{y} = 0$ gives $\vec{x} \perp \vec{y}$, but why ?
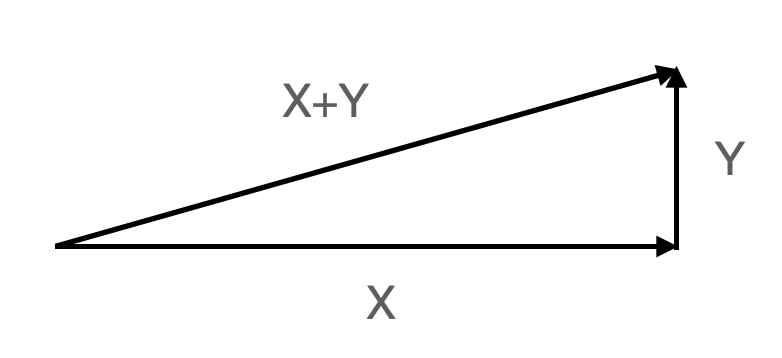
No matter which dimension we are in, we have this triangle if $x \perp y$
$$
\therefore |x|^2+|y|^2 = |x+y|^2
$$
$$
|x|^2 = x_1^2+x_2^n+…+x_n^2
$$
We can express this in matrix language
$$
|x|^2 = \vec{x}^T \vec{x}
$$
Example
$$
\vec{x} = \begin{bmatrix} x_1 \ x_2 \ … \ x_n \end{bmatrix}
$$
$$
|x|^2 = x_1^2+x_2^n+…+x_n^2
$$
$$
\vec{x}^T\vec{x} = \begin{bmatrix} x_1 & x_2 & … & x_n \end{bmatrix}
\begin{bmatrix} x_1 \ x_2 \ … \ x_n \end{bmatrix}
= x_1^2+x_2^n+…+x_n^2
$$
Deduction
$$
\because |x|^2+|y|^2 = |x+y|^2
$$
$$
\therefore \vec{x}^T\vec{x}+\vec{y}^T\vec{y} = (\vec{x}+\vec{y})^T(\vec{x}+\vec{y})
$$
$$
=(\vec{x}^T+\vec{y}^T)(\vec{x}+\vec{y})
$$
$$
= \vec{x}^T\vec{x}+\vec{y}^T\vec{y} + \vec{x}^T\vec{y} + \vec{y}^T\vec{x}
$$
$$
\therefore \vec{x}^T\vec{y} + \vec{y}^T\vec{x} = 0
$$
$$
\because \vec{x}^T\vec{y} = \vec{y}^T\vec{x} = x_1y_1 + x_2y_2+…+x_ny_n
$$
$$
\therefore \vec{x}^T\vec{y} = \vec{y}^T\vec{x} = x_1y_1 + x_2y_2+…+x_ny_n = \vec{x}\cdot \vec{y}=0
$$
So we can see that $\vec{0}$ is orthogonal to any vector
Orthogonal subspaces
If every vector in subspace X is orthogonal to every vector in subspace Y, then we say X is orthogonal to Y
With that definition, we can easily spot that $C(A^T) \perp N(A)$ and $C(A) \perp N(A^T)$
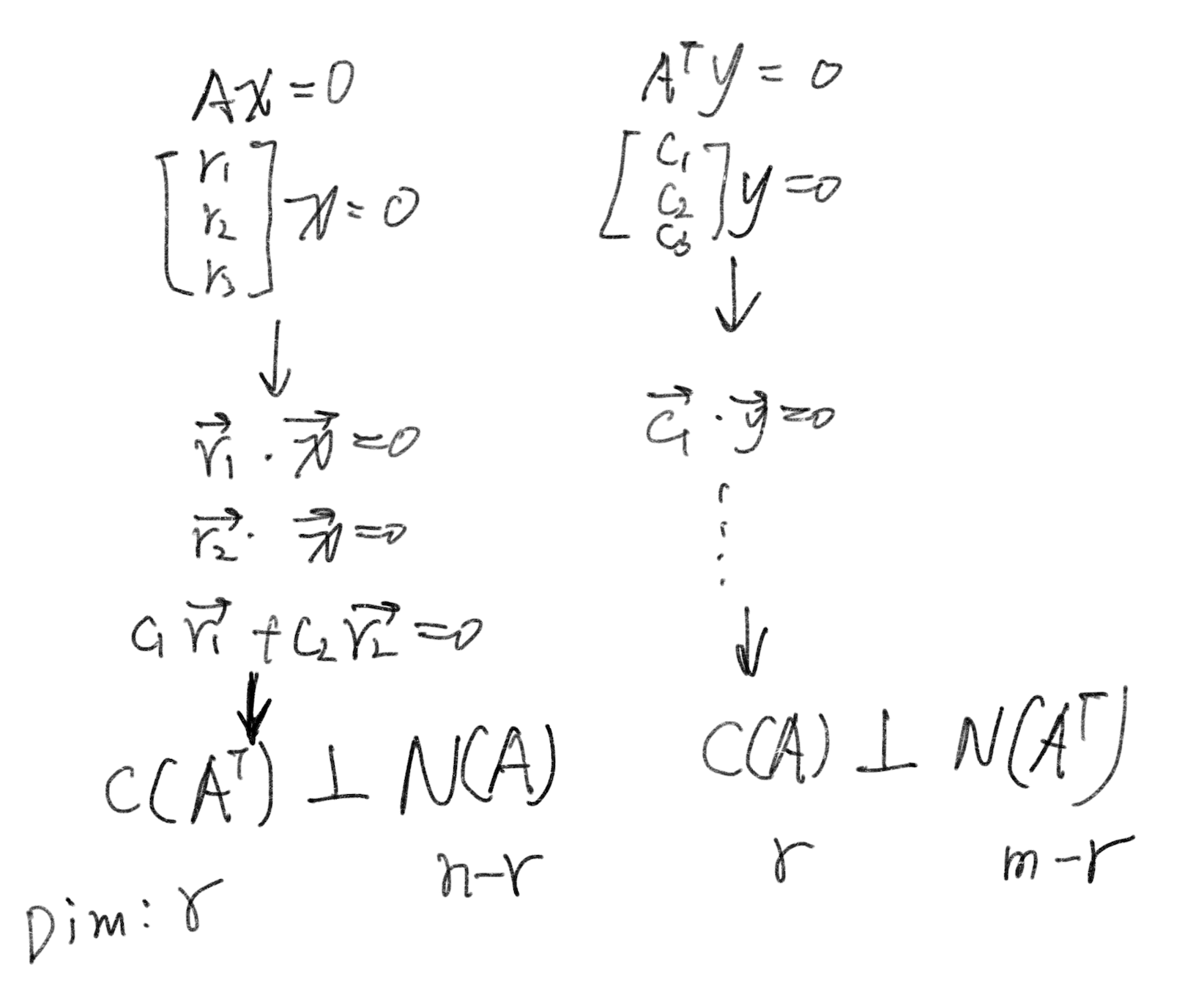
Projection

Now let’s express the projection operation in matrix language
The projection matrix
$$
P \vec{b} = \vec{p}
$$
$$
\therefore P\vec{b} = \frac{aa^T}{a^Ta}\vec{b}
$$
$$
\therefore P = \frac{aa^T}{a^Ta} ,a^Ta\text{ is a scalar}, aa^T \text{is a matrix}
$$
$$
\therefore P = \frac{1}{a^Ta} aa^T
$$
$P$ is symmetric($aa^T$),$P^T = P$
If we project $\vec{b}$ to $\vec{a}$ twice, we can see that the $\vec{p}$ doesn’t change, so $P^2=P$
$C(P)$ is a line through $\vec{a}$, we can see this from the graph, $P\vec{b}=\vec{p}$, so linear combination of $P$’s columns gives $\vec{p}$
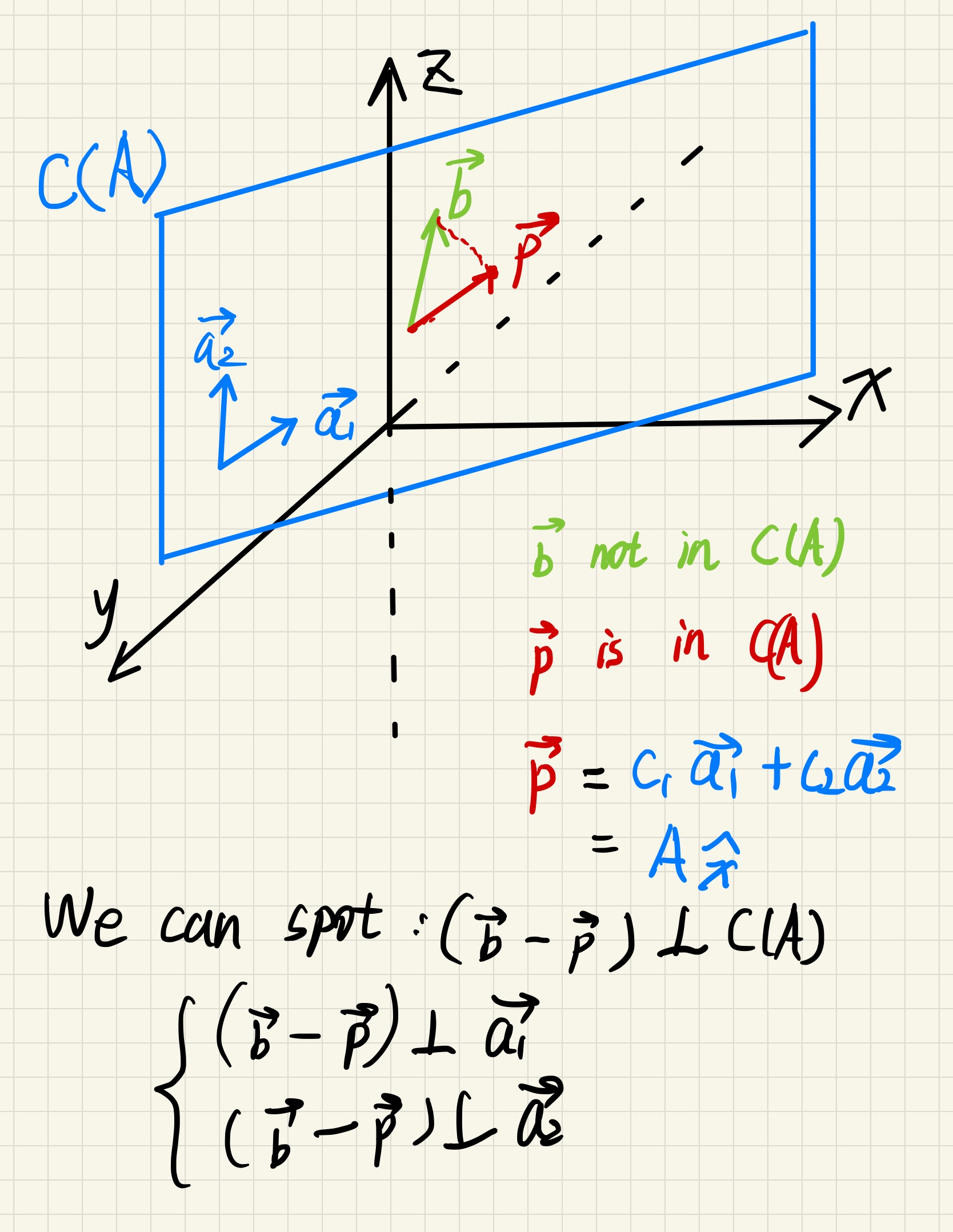
Why projection ?
Because when we cannot solve $Ax = \vec{b}$(some equations are “noise”, therefore $\vec{b}$ is not in $C(A)$) we need to find a close solution which $A^{x} = \vec{p}$, $\vec{p}$ is the projection of $\vec{b}$ onto $C(A)$
$^{x}$ is the way to combine $C(A)$’s basis that gives $\vec{b}$’s projection on $C(A)$
Two dimension example
$$
\therefore A^T(\vec{b}-A^{x})=0
$$
$$
\therefore A^TA^{x} = A^T\vec{b}
$$
We can also see that $\vec{b}-\vec{p}$ is in $N(A^T)$ which is perpendicular to $C(A)$
Solving
$$
^x = (A^TA)^{-1}A^T\vec{b}
$$
$$
\vec{p} = A^x= A(A^TA)^{-1}A^T\vec{b}
$$
If A is square and invertible matrix, projection of b to the whole space is b itself, so it’s ok for b=p, otherwise not
$$
P= A(A^TA)^{-1}A^T
$$
We can see $P^T = P$ and $P^2 = P$ are still hold
Application of projection
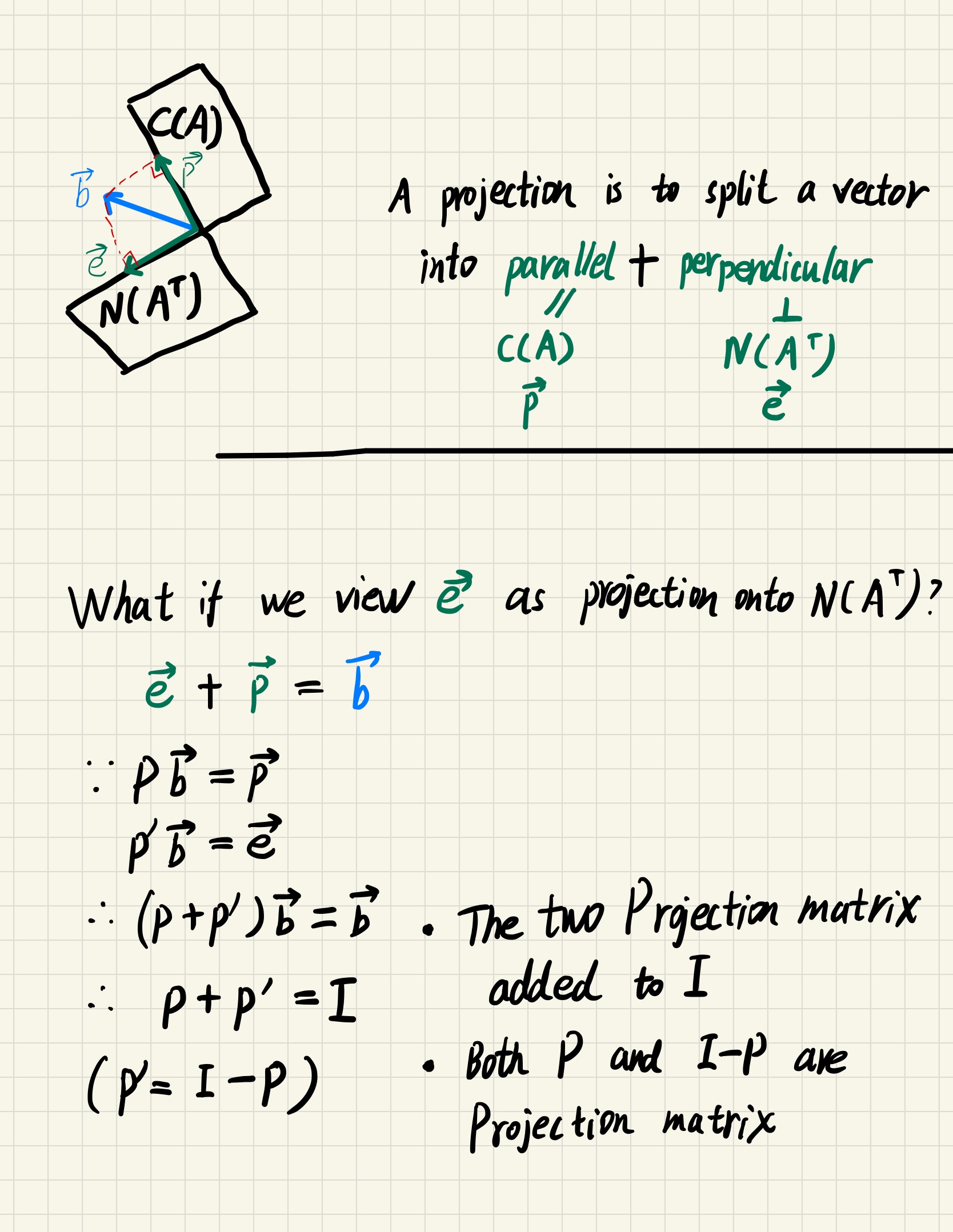
Try to find the line best fitting these points
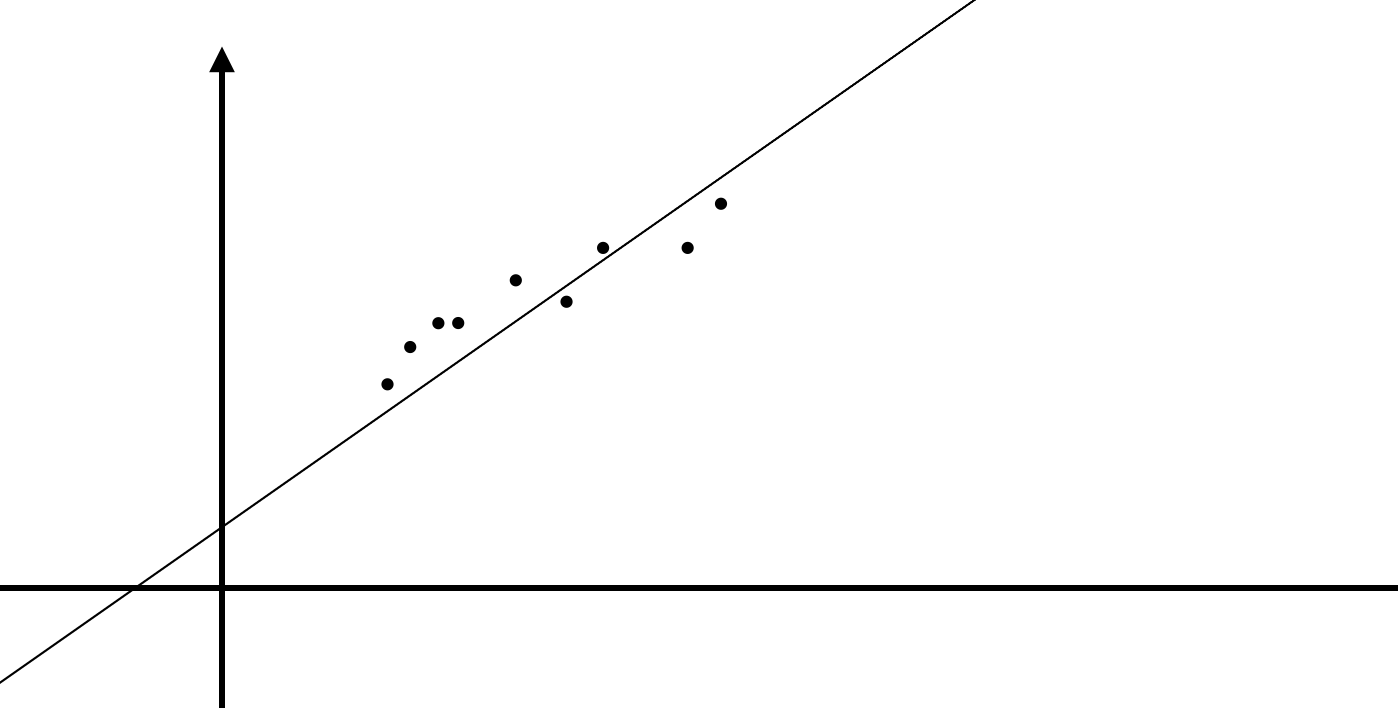
$$
assume , y = kx +t
$$
$$
\begin{bmatrix}
1& x_1 \
1 &x_2 \
…&…\
1 &x_n
\end{bmatrix}
\begin{bmatrix}
t \ k
\end{bmatrix} =
\begin{bmatrix}
y_1 \ y_2 \ … \ y_n
\end{bmatrix}
$$
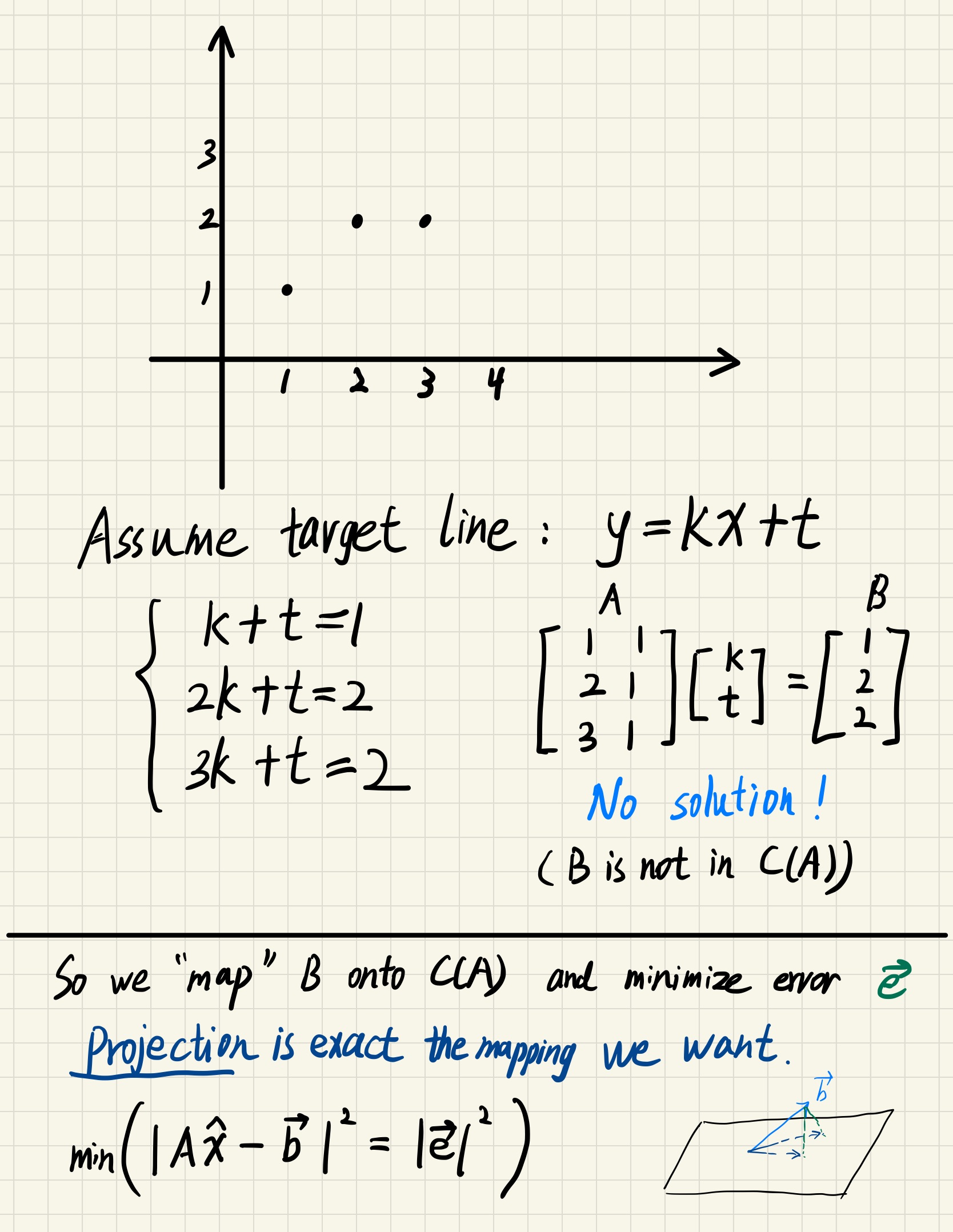
What is a best fit ?
Statistics call this linear regression
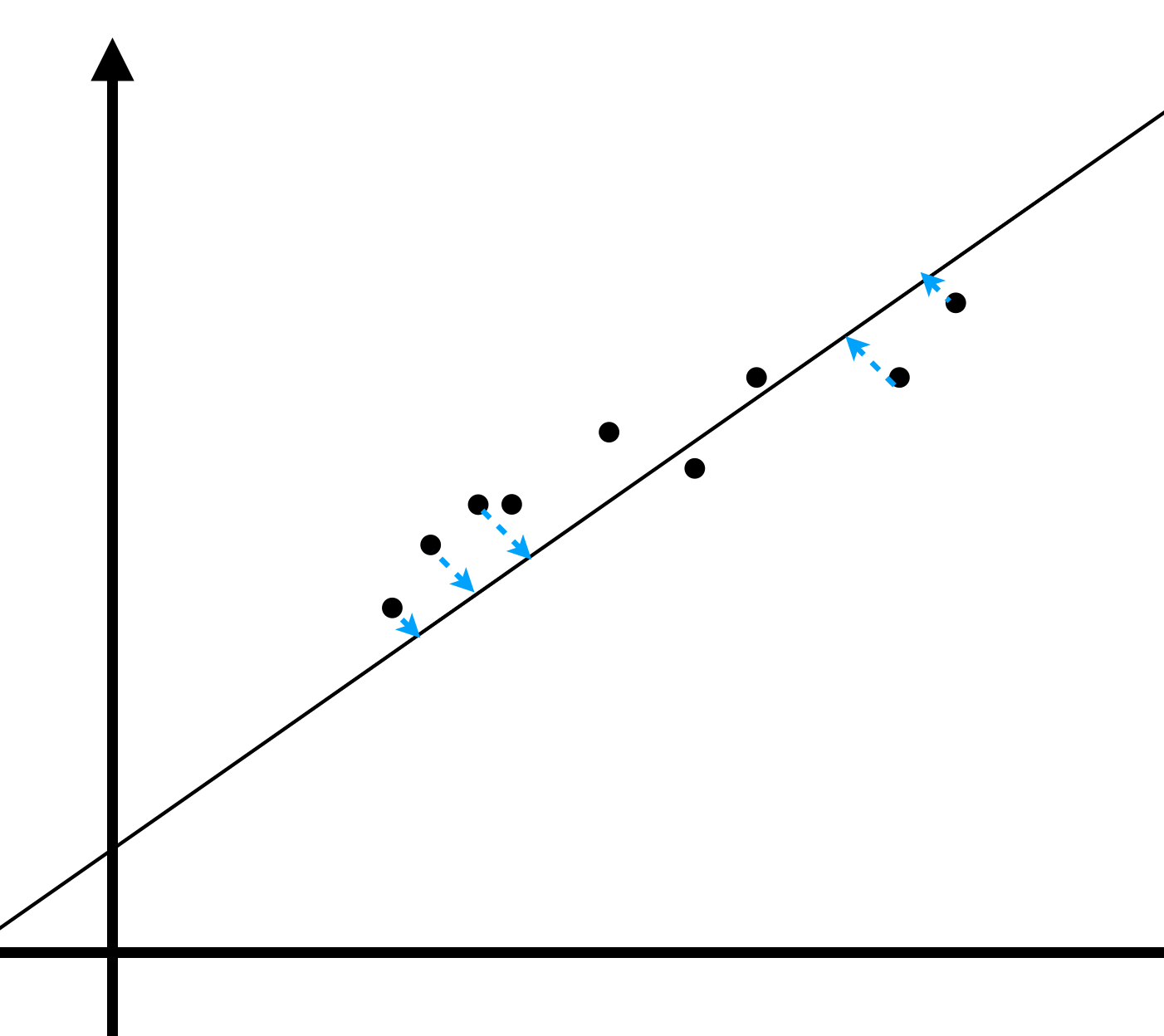
$$
Min(|e_1|^2 + |e_2|^2 + …+|e_n|^2)
$$
We can solve this from calculus perspective
$$
Min((k+t-1)^2 + (2k+t-2)^2+ (3k+t-2)^2) = Min(F)
$$
$$
\frac{\partial F}{\partial k} = 28k+12t-22=0
$$
$$
\frac{\partial F}{\partial t} = 12k+6t-10=0
$$
$$
\begin{cases}
k = \frac{1}{2}\
t = \frac{2}{3}
\end{cases}
$$
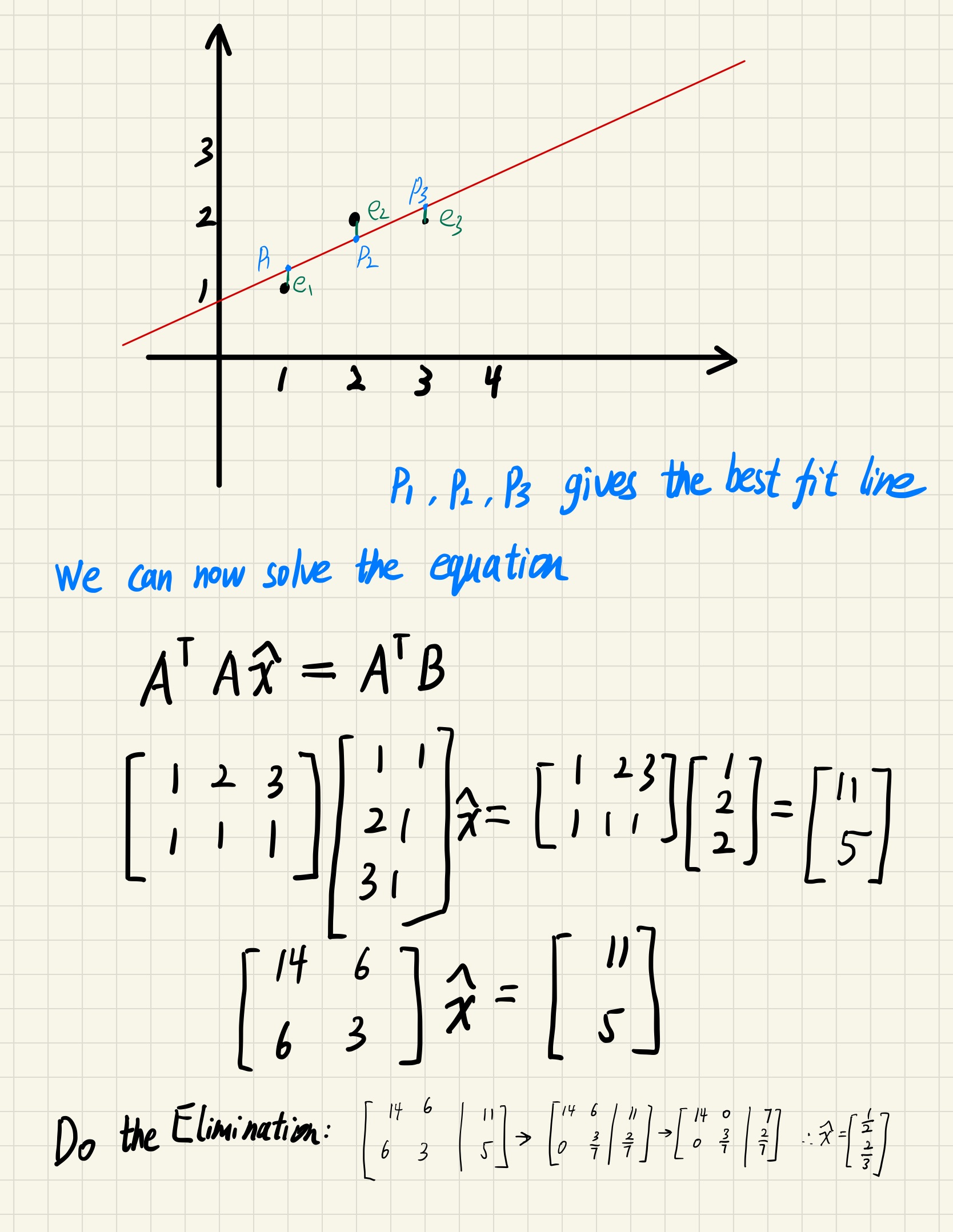
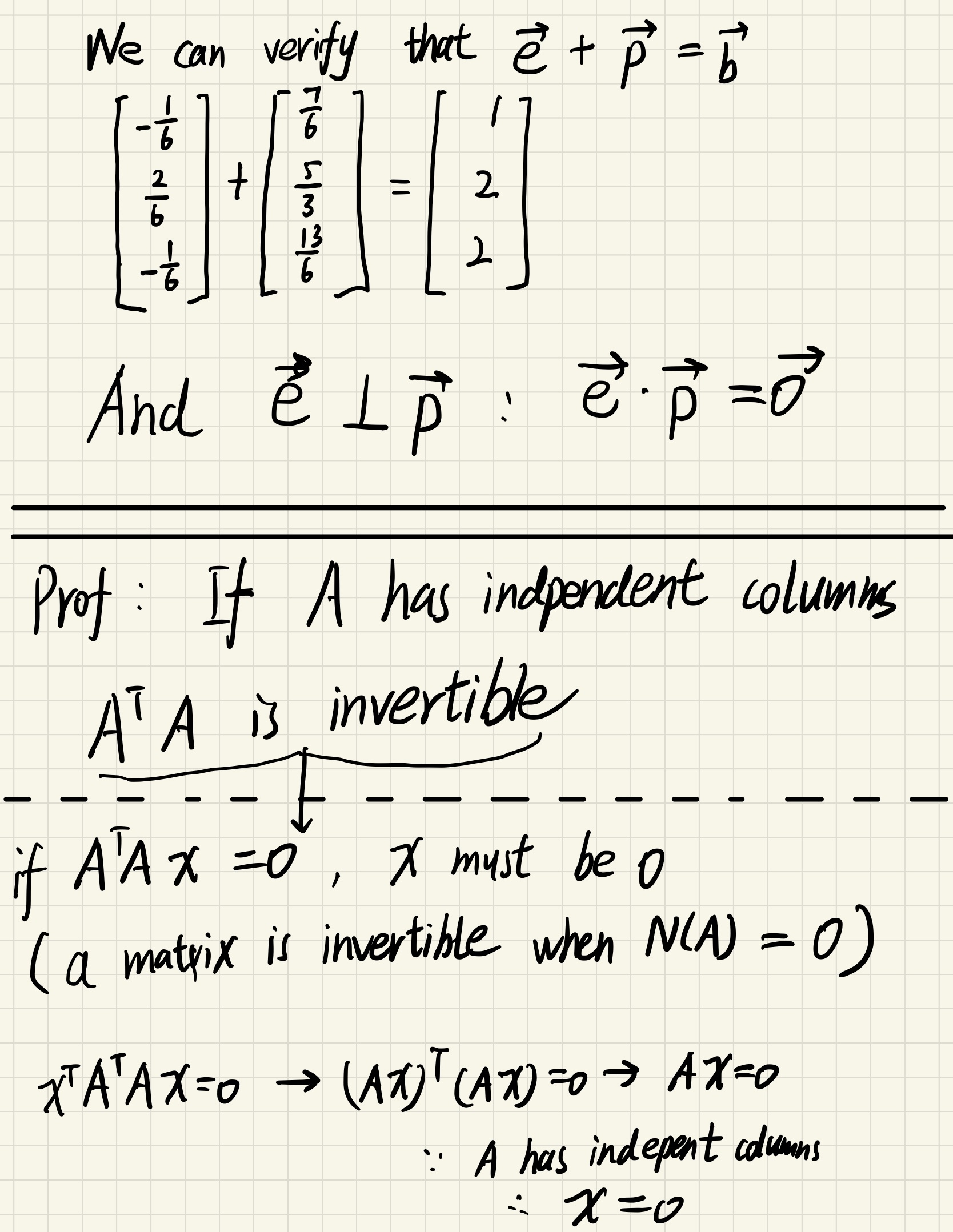
Ortho-normal vectors
linear algebra - In which cases is the inverse of a matrix equal to its transpose?
$$
\vec{i}^T \cdot \vec{j} = \begin{cases}
0 & , i \ne j\
1 & , i = j
\end{cases}
$$
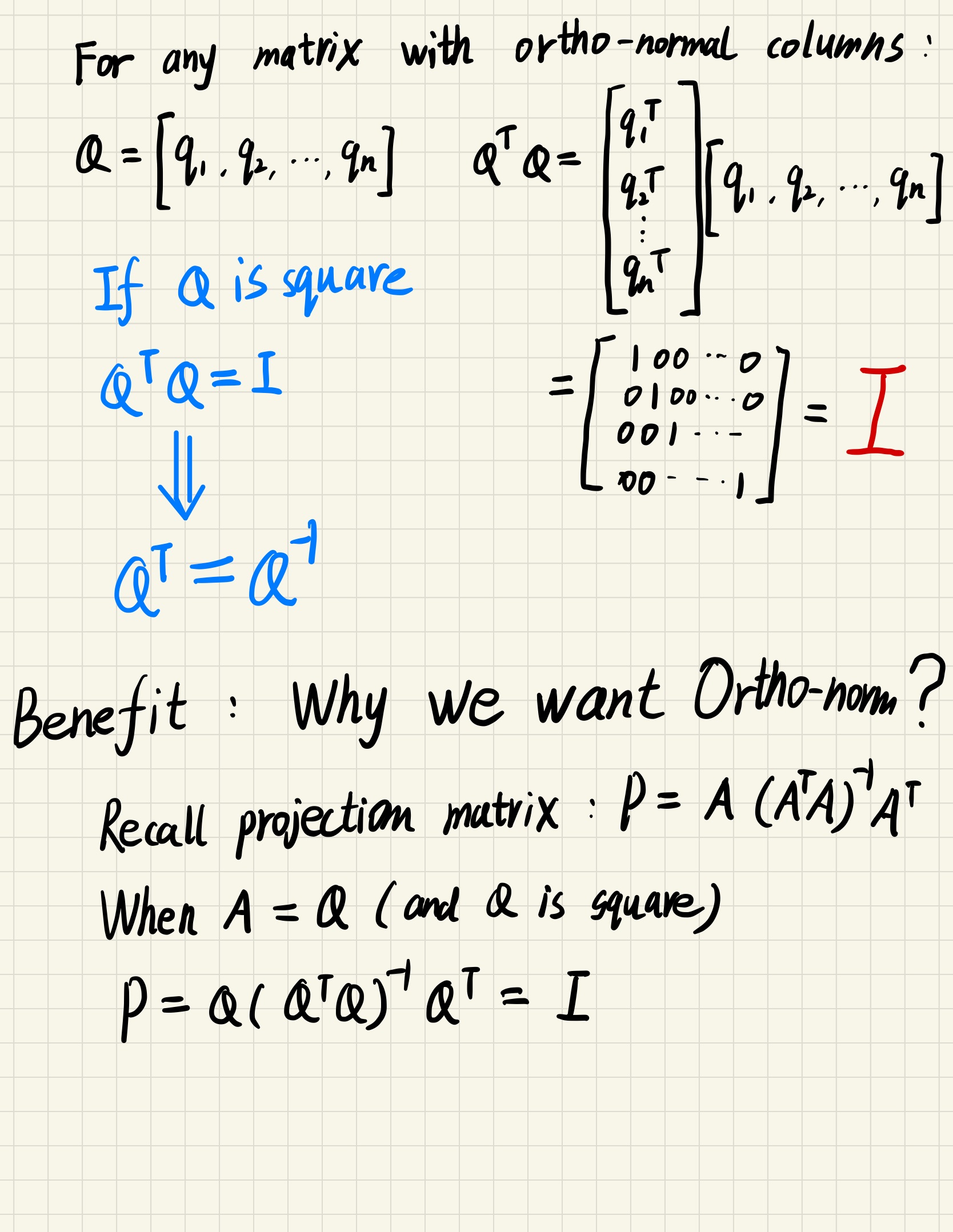
Gram-Schemit
turn independent vectors into ortho-normal vectors


Express in matrix language
$$
A = QR
$$
(since $Q$ is ortho-normal, when $Q$ is square, we can see $Q^{-1} = Q^T$)
$$
\therefore R = Q^TA
$$
1 | q,r = QRDecomposition( array([ [1,1],[1,0],[1,2]])) |