Square Matrix’s determinant
The value is called determinant since it packs lots of information of the matrix, nearly “determine” it
Only square matrix has determinant
A matrix is invertible if the determinant is non-0, noninvertible if is 0
$\det(I) = 1$
Exchange rows flip the sign of determinant
Determinants are “linear” only for each row
- $\forall A$, multiply one row by a scalar can be collected out
$$
\begin{vmatrix}
ta&tb\
c&d
\end{vmatrix}= t\begin{vmatrix}
a&b\
c&d
\end{vmatrix}
$$
- $\forall A$, add one row by another row can be done separately
$$
\begin{vmatrix} a+ a’ & b+b’\
c&d
\end{vmatrix} = \begin{vmatrix} a & b\
c&d
\end{vmatrix}+\begin{vmatrix} a’ &b’\
c&d
\end{vmatrix}
$$
- Two equal rows lead to $\det(A) = 0$
$$
Prof: \det(A) = -\det(A_{\text{swap row}} = A)
$$
$$
\therefore 2 \det(A)= 0
$$
- Gaussian Elimination will not change the value of determinant
$$
\begin{vmatrix} a + kc & b+kd\
c&d
\end{vmatrix} = \begin{vmatrix} a & b\
c&d
\end{vmatrix}+\begin{vmatrix} kc &kd\
c&d
\end{vmatrix} = \begin{vmatrix} a & b\
c&d
\end{vmatrix}+ k \cdot 0
$$
A row of 0s will give $\det(A) = 0$ (obvious)
Upper/Lower triangular matrixes’ determinant is product of diagonal
$$
\begin{vmatrix}
d_1 & * &…&*\
0& d_2 & …&*\
0&0&d_3…& *\
0&0&0…& d_n
\end{vmatrix} \stackrel{\text{back substitusion}}{=} \begin{vmatrix}
d_1 & 0 &…&0\
0& d_2 & …&0\
0&0&d_3…& 0\
0&0&0…& d_n
\end{vmatrix}
$$
$$
\stackrel{\text{extrac coefficients}}{=} \begin{vmatrix}
d_1 & 0 &…&0\
0& d_2 & …&0\
0&0&d_3…& 0\
0&0&0…& d_n
\end{vmatrix} = d_1 d_2 …d_n I = d_1d_2…d_n
$$
- $\det(AB) = \det(A)\det(B)$
$$
\text{usage}: \det(I = A^{-1}A) = \det(A^{-1})\det(A) = 1
$$
$$
\therefore \det(A^{-1}) = \frac{1}{\det(A)}
$$
- $\det(A^T) = \det(A)$
(Now all rules for rows hold for columns)
$$
\text{Prof}: \forall A , \text{if A is invertible}
$$
$$
A = LU
$$
$$
\therefore |A^T| = |U^T||L^T| = (d_1d_2…d_n)^2\
|A| = |L||U| = (d_1d_2…d_n)^2
$$
Formula for determinant
The Big formula
$$
\det(A) = \sum_\text{all permuation of n} \det(P) \cdot a_{1\alpha}a_{2\beta}…a_{n\gamma} , (\alpha,\beta,…,\gamma \text{are all permuation of n})
$$
$$
\det(P) = 1 \text{or} -1
$$
Three dimension example

Cofactors
Before using cofactor formula, you can do elimination or exchange first to simplify

Application of determinant
Inverse matrix
$$
A^{-1} = \frac{1}{|A|} C^T
$$
$$
Prof \because AA^{-1} = I
$$
$$
\therefore A \frac{1}{|A|} C^T = I
$$
$$
\therefore AC^T = |A|I
$$
$$
\because C = \begin{bmatrix}
c_{11} & c_{12} & … & c_{1n} \
c_{21} & … & … &…\
… & … & … &…\
c_{n1} … &…& … & c_{nn}
\end{bmatrix}
$$
$$
\therefore AC^T = \begin{bmatrix}
|A| & 0 & … & 0 \
0 & |A| & … &…\
… & … & … &…\
0 … & … & …& |A|
\end{bmatrix} = |A|I
$$
Cramer’s Rule
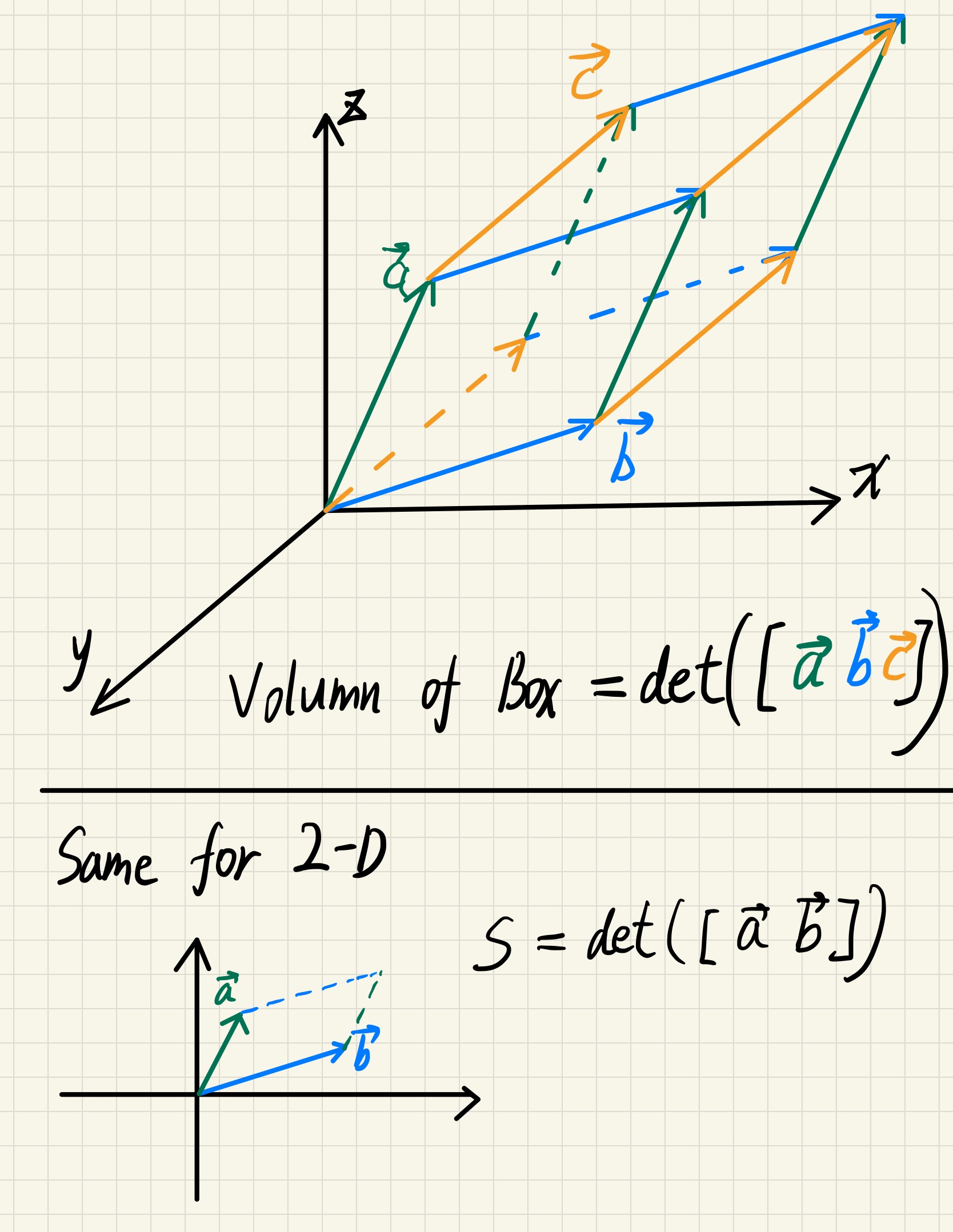
Geometry Application