Eigen Vector and Eigen Value
Let’s view matrix like function in calculus
$y = f(x)$, x goes in , $f(x)$ comes out
$y = A\vec{x}$ , $\vec{x}$ goes in, $A\vec{x}$ comes out
Eigen vectors are where $A\vec{x} \parallel \vec{x}$
$$
A\vec{x} = \lambda \vec{x}
$$
Eigen vectors for a matrix $A$ do not change direction after $A$ applied on it
Eigen value is the $\lambda$
How to find Eigen vectors and Eigen value
sum of trace = sum of eigenvalues
product of eigenvalues = determinant
the rank of a matrix can be defined as being the num- ber of non-zero eigenvalues of the matrix
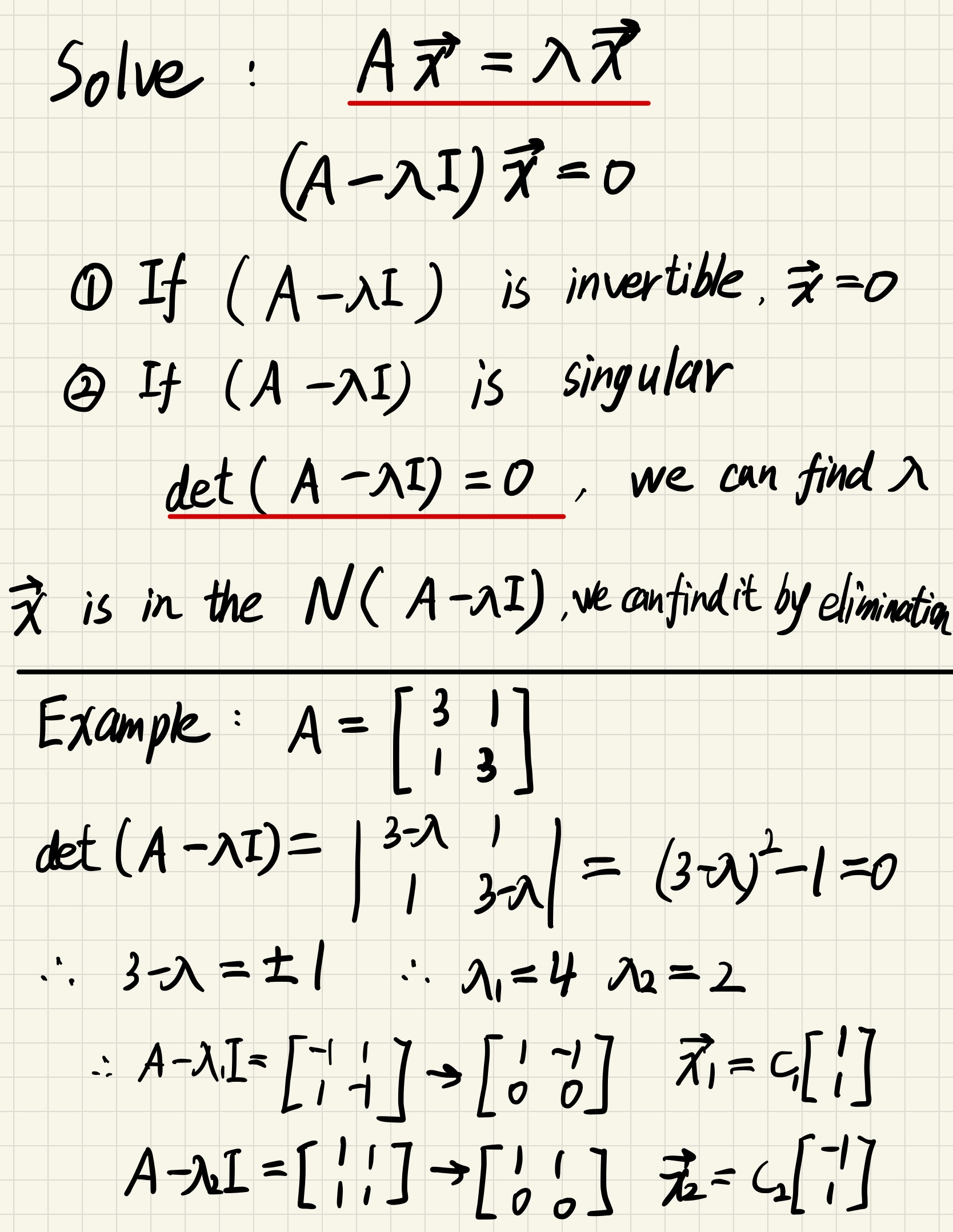

Application of Eigen values and Eigen vectors
Replace a matrix $A$ with a Eigen value $\lambda$
$$
S^{-1}AS=\Lambda
$$

We can also obtain rule for power n
$$
A^n = S \Lambda^n S^{-1}
$$
This is the best way to investigate $A^n$
However, if we want to use this formula, we see that the Eigen vectors must be independent
Theorem : If all Eigen values are different, then the Eigen vectors are independent
Solving recursion

The Eigen value represent the growing speed of $A$ in each direction given by the Eigen vector !