They are definitely positive
More about symmetric matrixes

Positive Definite Matrixes
Bring the whole course together
They are symmetric
All Eigen values are positive
All pivots are positive
All sub-determinants are positive
Test : How can I tell if a matrix is positive definite or not ?
2 by 2 case :
$$
A = \begin{bmatrix} a & b \ b & d \end{bmatrix}
$$
Eigen values : $\lambda_1 > 0 \land \lambda_2 > 0 ?$
Pivots : $a > 0 \land \frac{ac-b^2}{a} > 0$
Sub-determinants : $|a|>0 \land \begin{vmatrix} a & b \ b & d \end{vmatrix}>0$
$\vec{x}^T A \vec{x} > 0 $ , $\vec{x}$ should be any vectors(except $\vec{0}$)
Example:

Positive definite
Non-positive definite

But it is not easy for us to tell how the graph look like
We see that all quadratic form goes through $(0,0,0)$.
So we only need to see when they go out of the origin, it grows “upwards” in all directions or “downwards” in some directions (The partial derivatives).
And it finally turn out that we only need to look at the directions that Eigen vectors point to.
Connection with calculus
$(0,0,0)$ should be the minimum value for $z=f(x_1,x_2,…,x_n)$
In calculus:
all first order partial derivative = 0
second order partial derivative > 0
In linear algebra
all first order partial derivative = 0
Matrix of second order partial derivate is positive definite
$$
\begin{bmatrix}
f_{xx}& f_{xy} \
f_{yx} & f_{yy}
\end{bmatrix}
$$
Recall that $f_{xy} = f_{yx}$ (so we have 二元无条件极值$\Delta$法)
3 by 3 example
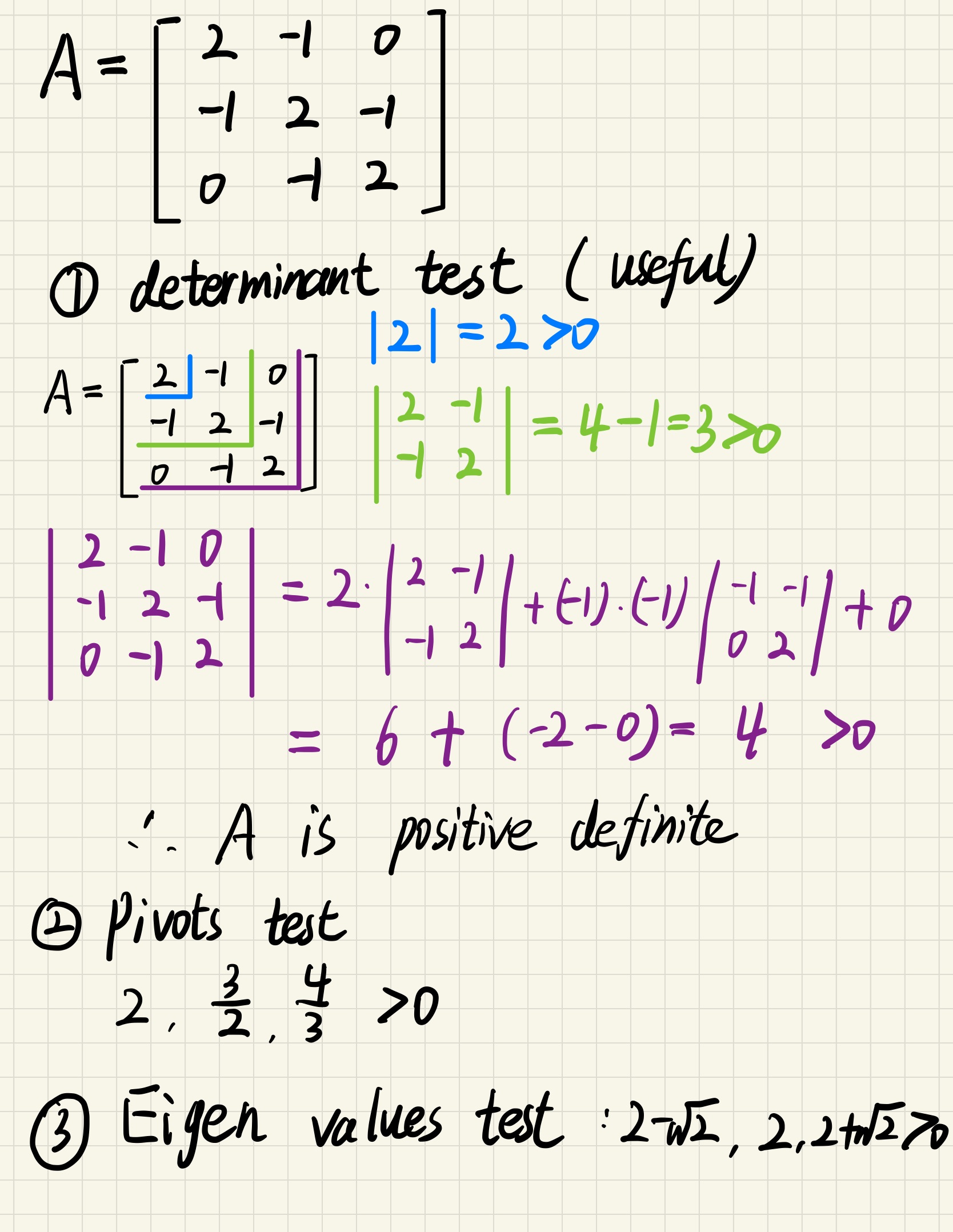


Similar matrixes
$A$ and $B$ are both *n * n matrixes* and they are similar when
$$
\exist M , B = M^{-1} A M
$$
So recall $A = S^{-1} \Lambda S$, so $A$ is similar to $\Lambda$
Why they are “similar”
Similar matrixes all have the same Eigen values
$$
Prof \ \because A\vec{x} = \lambda \vec{x}
$$
$$
\therefore AMM^{-1} \vec{x} = \lambda \vec{x}
$$
$$
\therefore M^{-1}AMM^{-1} \vec{x} = \lambda M^{-1}\vec{x}
$$
$$
\therefore B M^{-1} \vec{x} = \lambda M^{-1}\vec{x}
$$
$$
\therefore let M^{-1}\vec{x} = \vec{x’} ,\text{Eigen vectors for B}
$$
$$
\therefore B\vec{x’} = \lambda \vec{x’}
$$
A and B have the same Eigen value but different Eigen vectors