Math►Statistics

Introduction

MIT RES.6-012

introduction-to-probability

course link

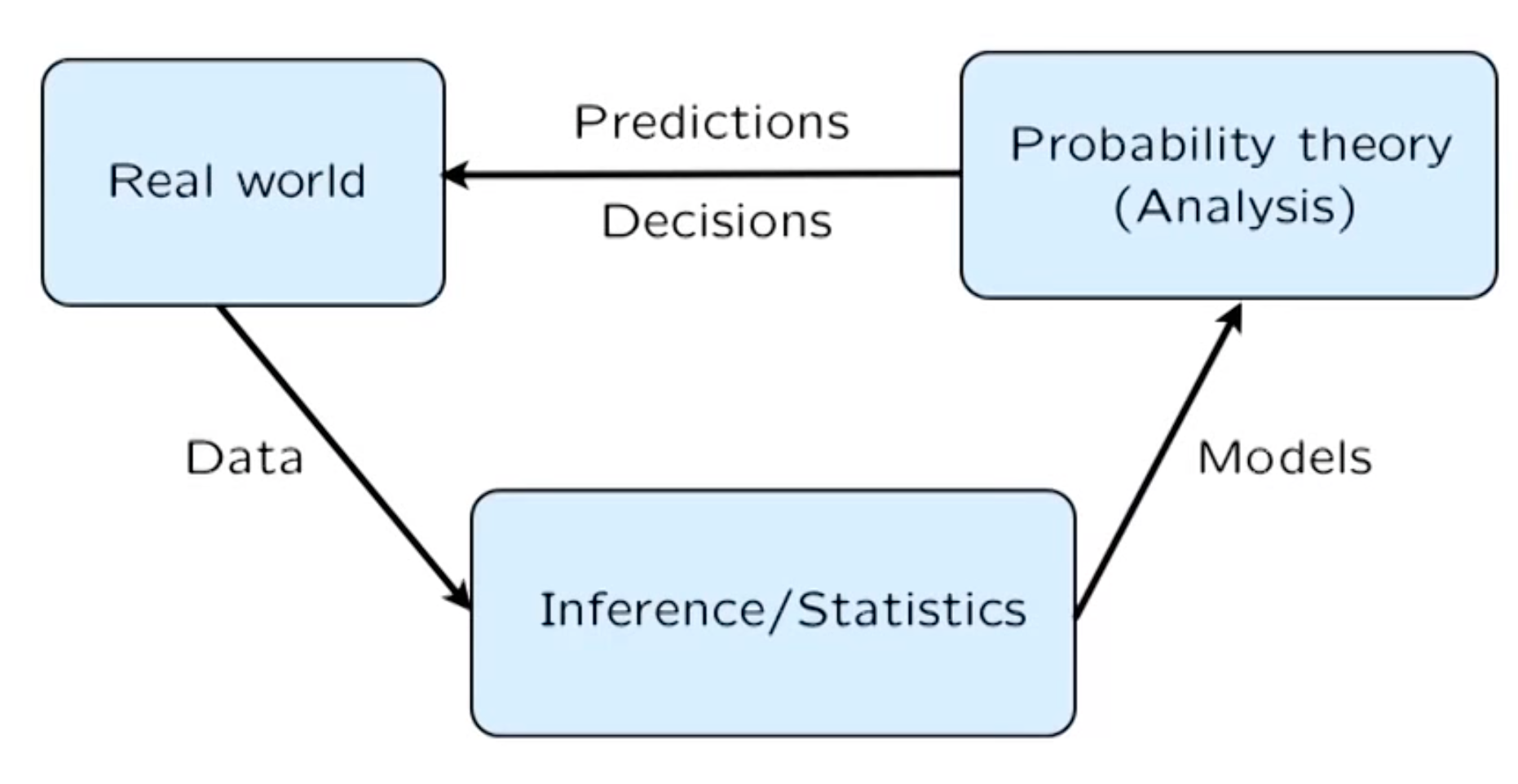
Overview of all element of the probability model

  • Sample space

  • probability laws

  • interpretation of probability

Sample space

All possible outcome of an activity/experiment, represented as a set.

Example

$$
\Omega(\text{flip a coin}) = {\text{heads},\text{tails}}
$$

$$
\Omega{(\text{roll a die})} = { 1,2,3,4,5,6 }
$$

Property

  • mutual exclusive (exact one outcome could happen at one experiment)

  • collectively exhaustive (the set include all possible outcomes)

  • At right granularity (do not include irrelevant details and mix experiment)

Look at the coin flipping example again, we can also have a sample space of

$$
\Omega(\text{flip a coin})={ \text{heads and rainy outside},\
\text{heads and no rain} , \text{tails and rainy} , \text{tails and no rain} }
$$

If we are investigating the connection of weather and coin, this space space could be right, but otherwise we would better choose a “simple” one and removing all weather information.

More examples
Sequential outcome

if the result of a experiment happen in “stage”/“phase” we can describe it by a tree

Say we roll a die twice

1
2
3
>>> SampleSpace = [(k,v) for k in range(1,7) for v in range(1,7)]
>>> SampleSpace
[(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)]

What is the chance of predicting the outcome of a die roll? : r/askscience

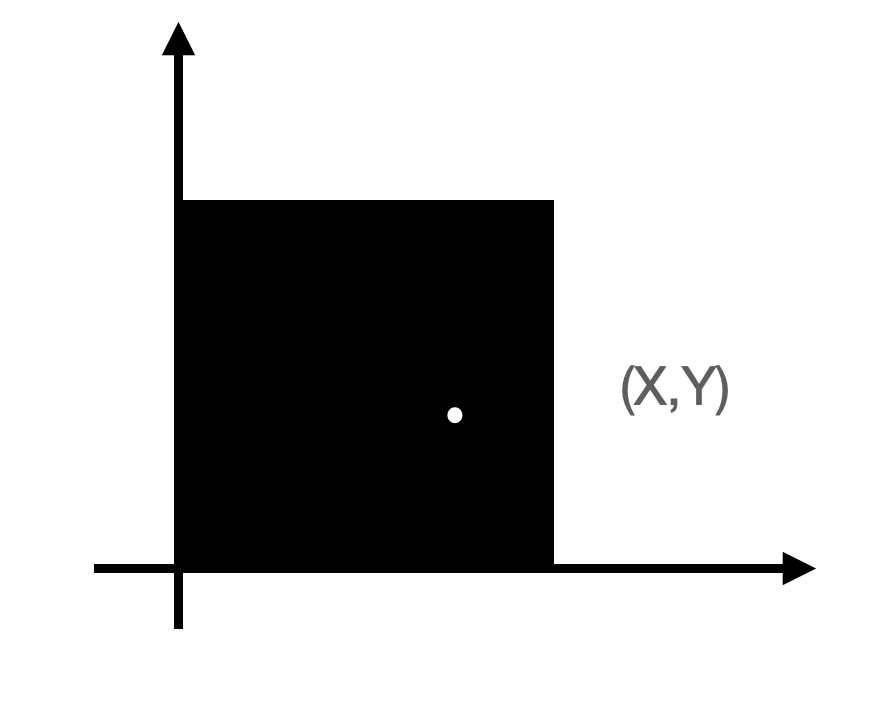
Continuous example

the sample space can be continuous and contain infinite outcomes

Say we throwing a dart to the unit square in a 2 by 2 plane

continuous

$$
\Omega = { (x,y) | 0 \le x \le 1 \land 0 \le y \le 1}
$$

Probability axioms

We only need 3 axioms to construction out models

probability is the likelihood of a/some specified outcome will occur in one experiment

Trouble

In the following case, what is the probability of the dart hit exactly the white point ?

continuous

Since there are infinite points in this area, the precision will always be 0

$$
P(\text{hit white point}) = 0
$$

Solution

Instead of assigning probability to each individual outcome we assign probability to a subset of the whole set, that is, a subset of outcomes.

$$
P(\text{hit upper half}) = \frac{1}{2}
$$

We call this subset an event. In an experiment if the outcome is in the subset, we say that the event happened, otherwise event not happened.

Axioms

  • Nonnegative : $P(A) \ge 0$

  • Normalization : $P(\Omega) = 1$

  • Additivity : $if A \cap B = \emptyset, then P(A \cup B) = P(A) + P(B)$

Deduction

Draw the graph before your proving !!!

  • $P(A) + P(\bar{A}) = 1$

$$
\because A \cap \bar{A} = \emptyset , A\cup \bar{A} = \Omega
$$

$$
\therefore P(\Omega) = P(A\cup \bar{A} ) = P(A) + P(\bar{A}) = 1
$$

  • $P(A) \le 1$

$$
\because P(A)=1 - P(\bar{A}), P(\bar{A}) \ge 0
$$

$$
\therefore P(A) \le 1
$$

  • $P(\emptyset) = 0$

$$
\because 1 = P(\Omega) + P(\bar{\Omega}) = 1 + P(\emptyset)
$$

$$
\therefore P(\emptyset) = 0
$$

  • for disjoint A,B,C,… $P(A\cup B\cup C …) = P(A)+P(B)+P(C)+…$

So we have the way to compute the probability of an event A

$$
P(A) = P({a_1}) + P({a_2}) + … + P({a_n}) = P(a_1) + P(a_2) + … + P(a_n)
$$

prof

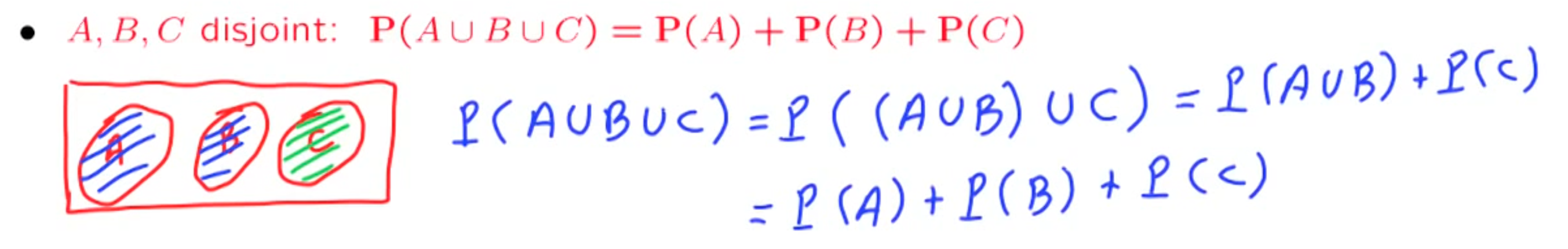
  • $if A \subseteq B , then P(A) \le P(B)$

$$
\because P(B)= P( A \cup (B-A)) , A \cap (B-A) = \emptyset
$$

$$
\therefore P(B)=P(A)+P(B-A) \ge P(A)
$$

  • For non-disjoint set A,B, $P(A\cup B) = P(A)+P(B) - P(A\cap B)$

prof

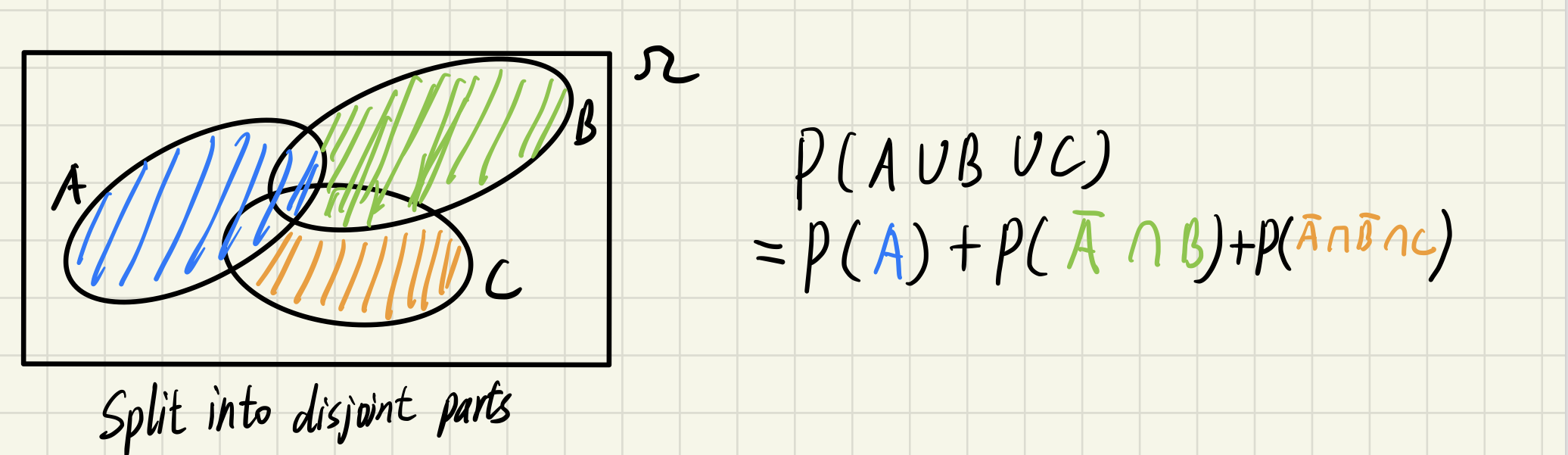
three

  • For infinite discrete disjoin subsets, if all events/subsets can be written as a sequence then the additivity law will still hold

$$
P(A_1 \cup A_2 \cup … ) = P(A_1) + P(A_2) + …
$$

Examples

Suppose we flip a coin, record the number of flipping before heads first appear

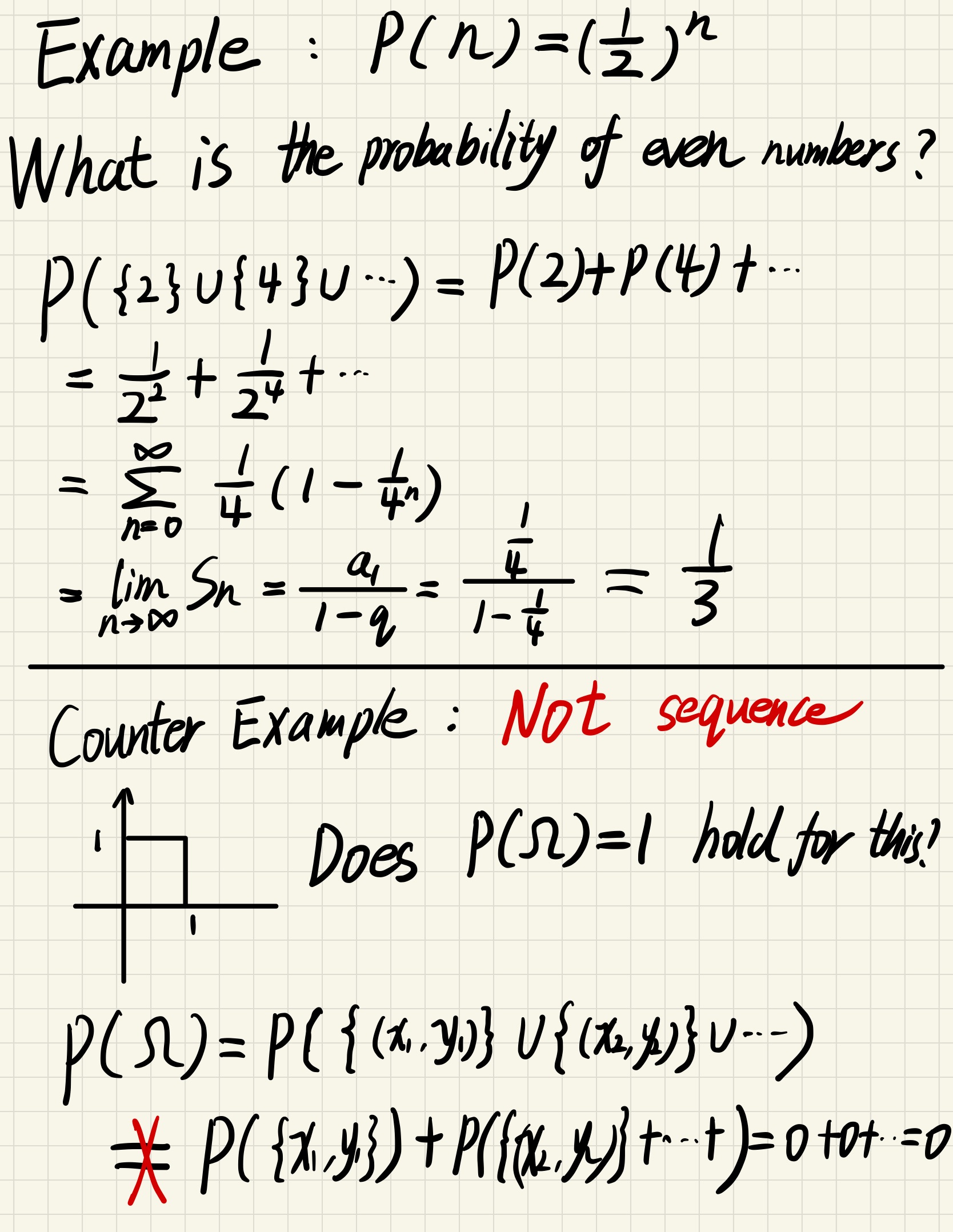
examples

Summary

What is probability

  • a bunch of mathematics (meaningless)

  • the frequency of the event( how often will it happen in infinite times of experiments?)

  • Probability does not tell us exactly what will happen, it is just a guide (Probability says that heads have a 1/2 chance, so we can expect 50 Heads. But when we actually try it we might get 48 heads, or 55 heads … or anything really, but in most cases it will be a number near 50.)

  • a framework of analyzing uncertain outcomes

summary