Conditioning and Bayes’s rule
we have some basic probability first and then use more information about the experiment/outcome to make the probability more reliable
Three important tools
Multiplication rules
Total probability theorem
Bayes’ rule (This is how we do inference)
Conditioning
using new information to revise the model
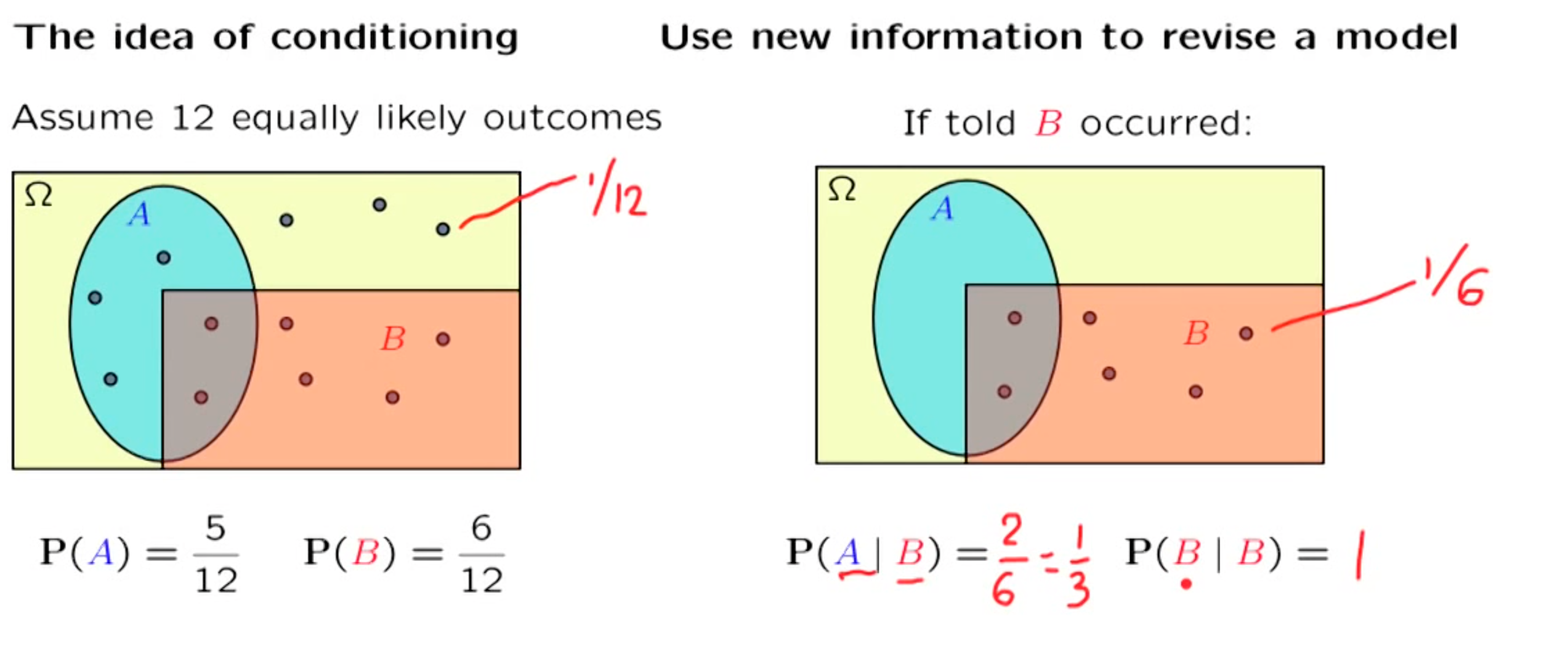
Definition
This is just a definition, we define things to be like this
$$
P(A|B) : \text{probability of A given that B has occurred}
$$
$$
P(A|B) = \frac{P(A\cap B)}{P(B)}
$$
Probability axioms still hold for conditional situation
The theorems in normal probability will all hold for conditional probability
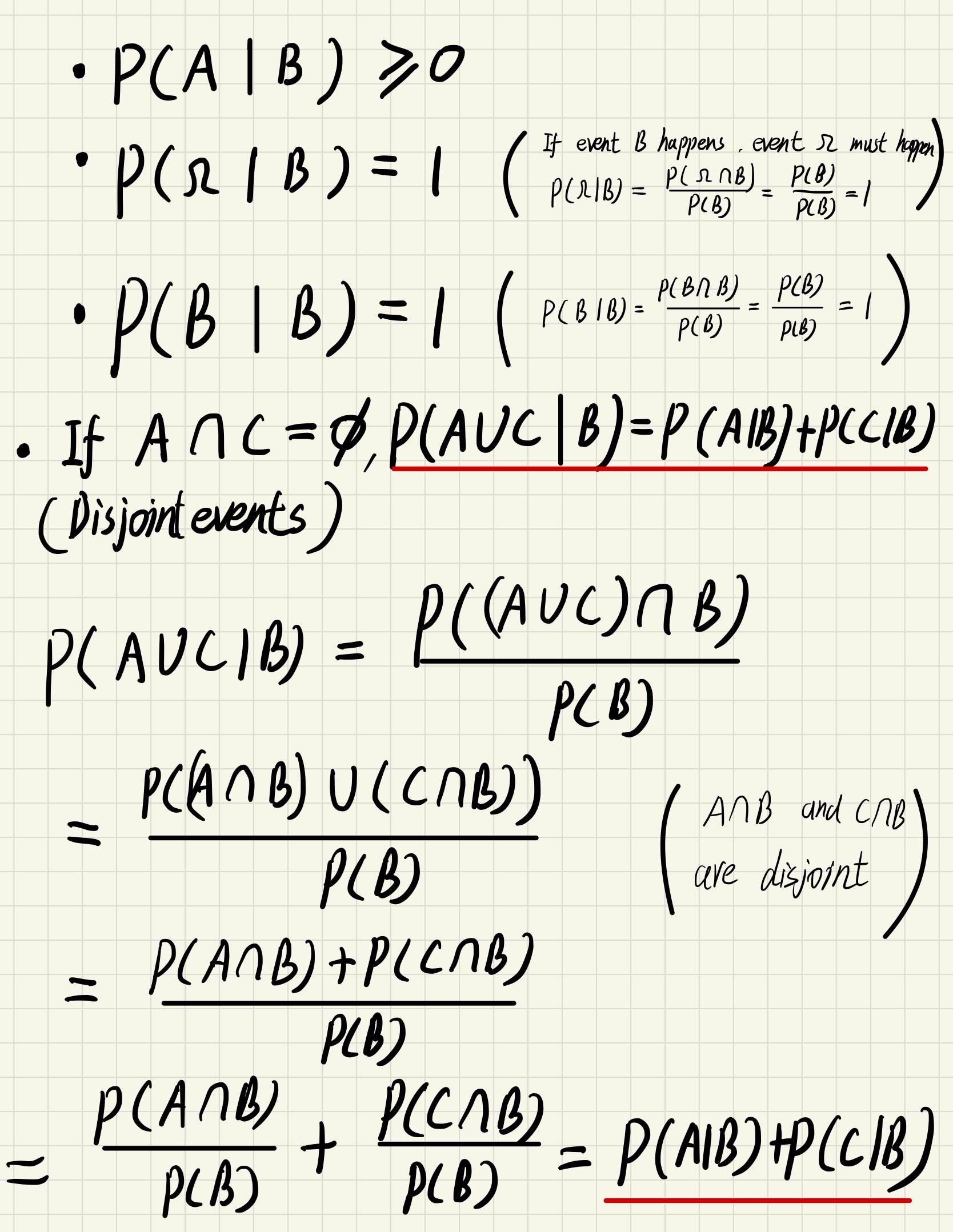
Application of conditional probability
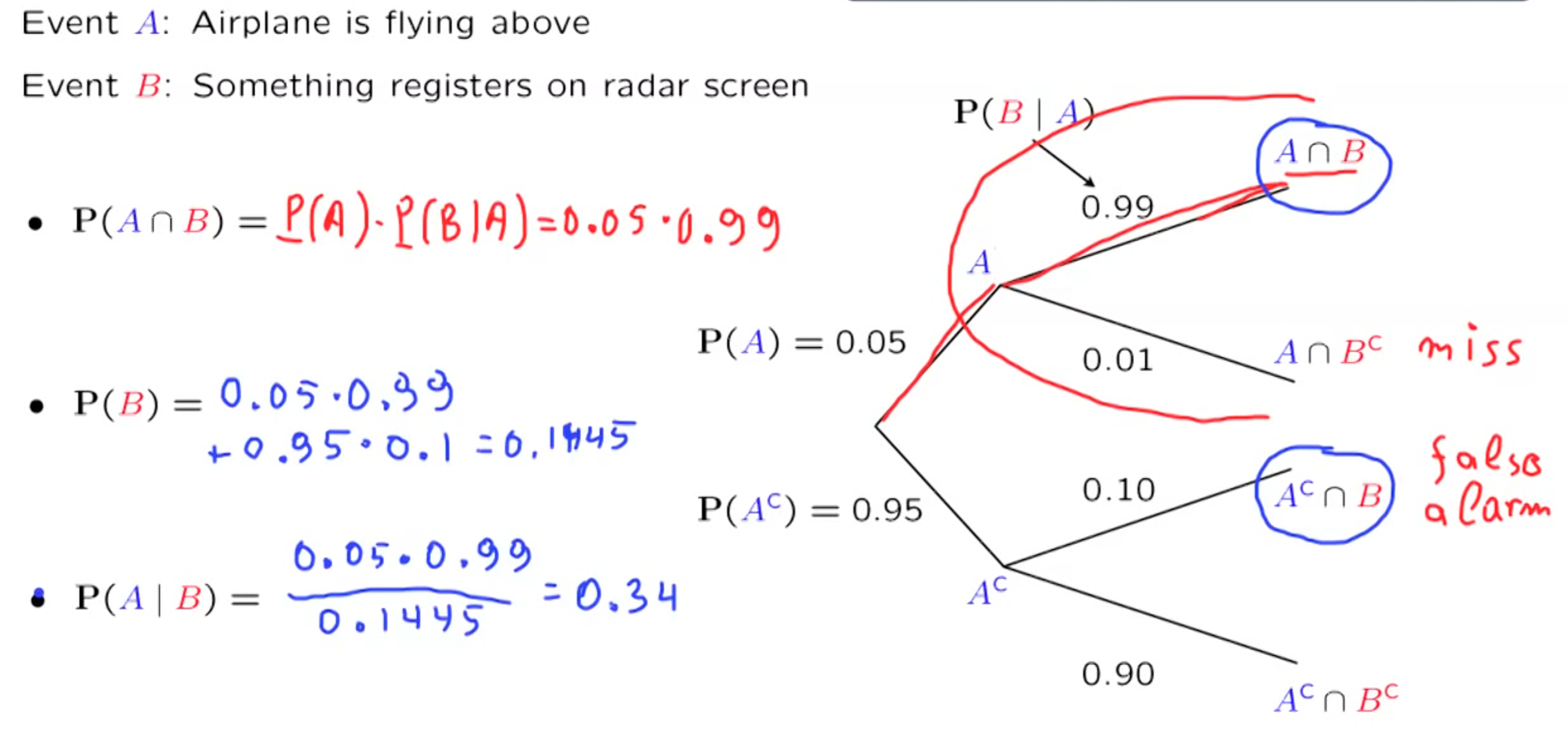
Multiplication Rule
$$
P(A \cap B) = P(A)P(B|A) = P(B)P(A|B)
$$
(This is reasonable, the probability of event A and B both happen is probability of A happens times probability of the probability of B when A happens)
Let’s do threesome
$$
P(A \cap B \cap C) = P( A\cap (B \cap C )) = P(A)P(B \cap C | A)
$$
$$
= P((A \cap B ) \cap C ) = P (A\cap B) P(C | A \cap B) = P(A)P(B|A)P(C | A \cap B)
$$
It can be more
$$
P(A_1 \cap A_2 \cap … \cap A_n) = P(A_1)P(A_2|A_1)P(A_3|A_1 \cap A_2)P(A_4 | A_1 \cap A_2 \cap A_3 )…
$$
Total Probability Theorem
The probability of an event is the sum of probability of all ways it can occur(under different situations)
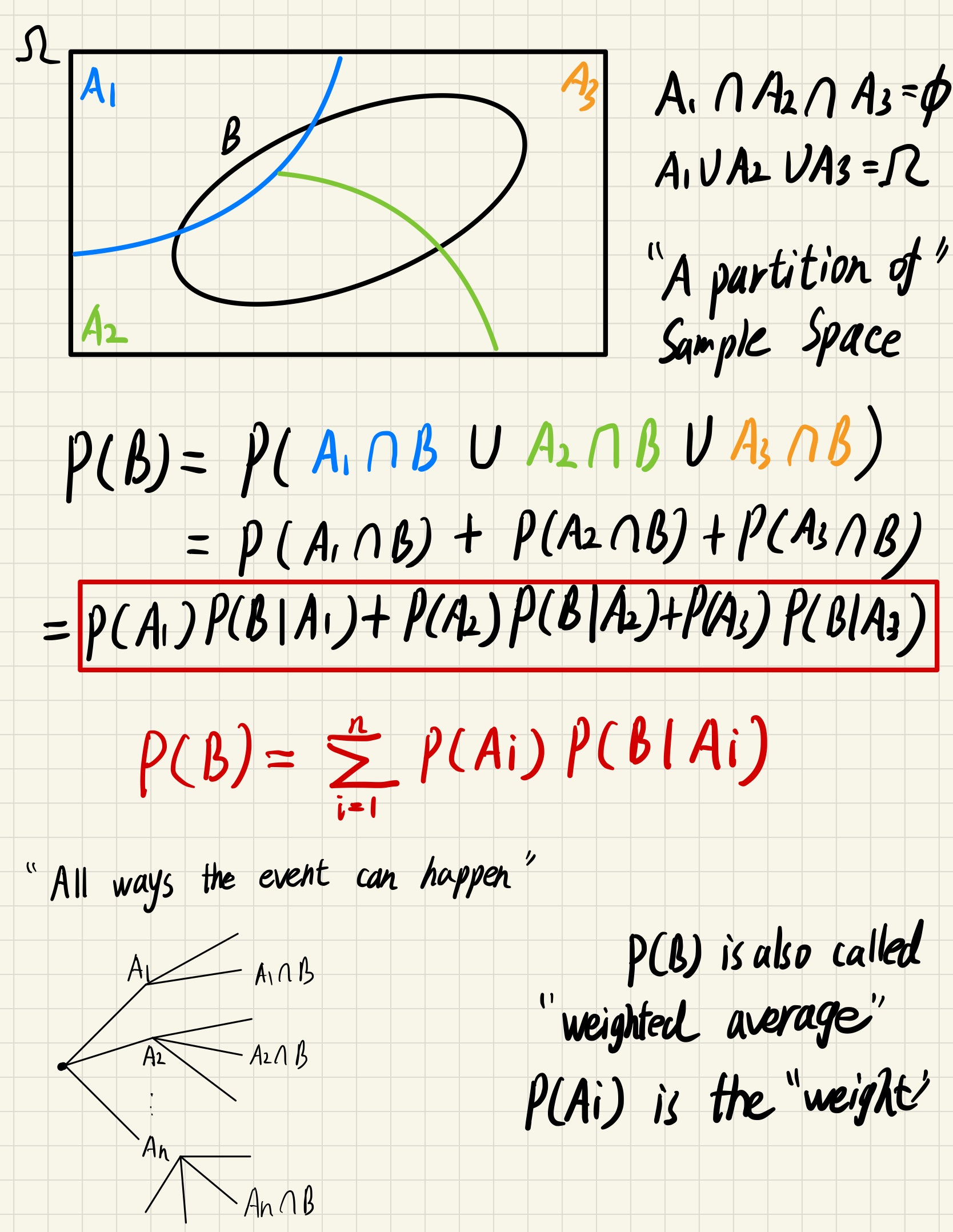
Bayes’ rule
A systematic way to incorporate new evidence
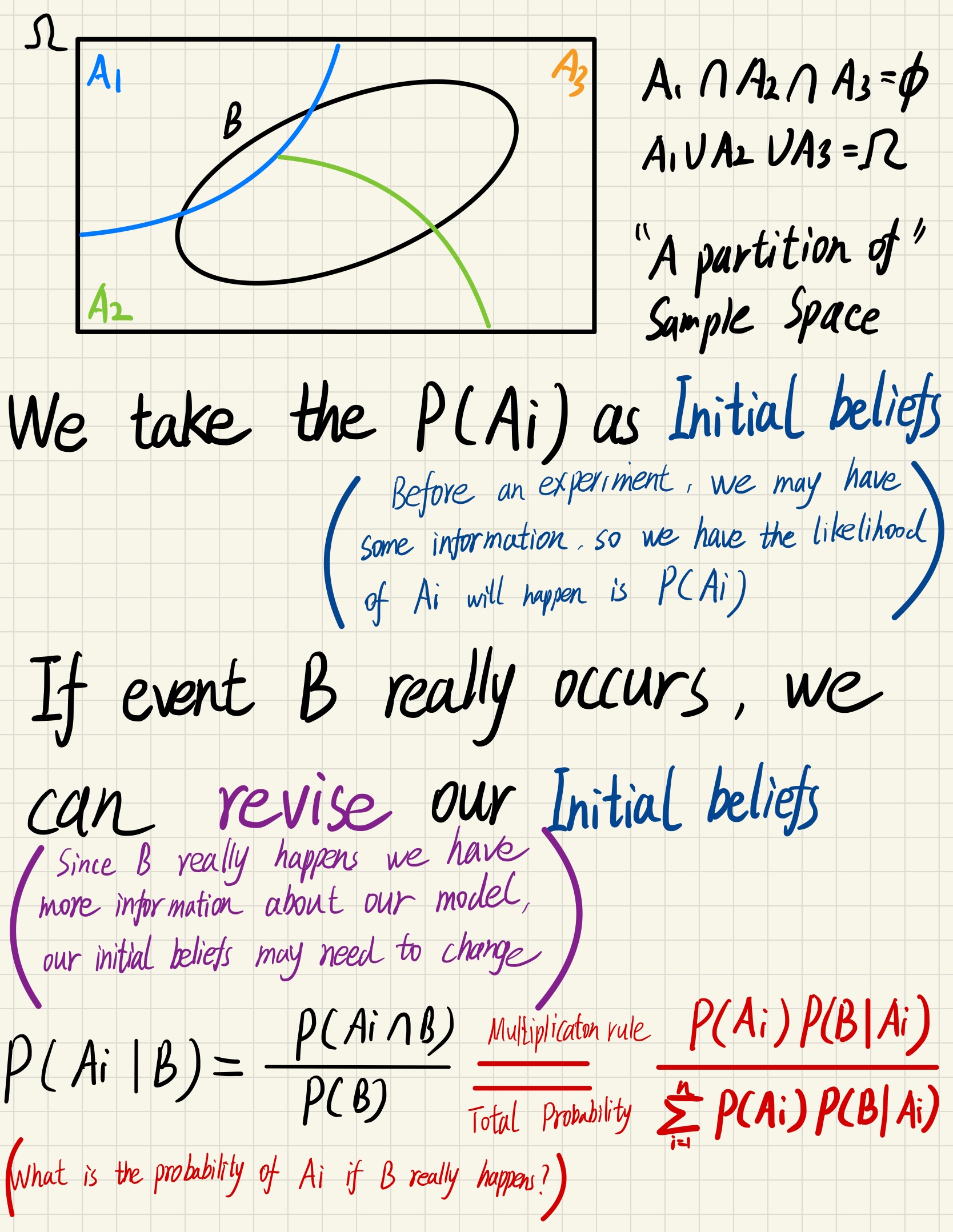
We can now infer how the initial situation could be like if B really happens, this is how Bayesian inference work.
