Independence
If event A really happens, it does not change the probability of B( P(B) == P(B|A) ), we say A doesn’t carry any useful information about B, A and B are independent
For example, if we toss a coin twice, the first tossing result will not affect the second tossing result. We call these two event independent
Deduction
$$
\because P(A|B) = P(A)
$$
$$
\therefore P(A|B) = \frac{ P( A \cap B ) }{P(B)} = P(A)
$$
$$
\therefore P(A \cap B) = P(A) P(B)
$$
Definition
If $P(A\cap B) = P(A)P(B)$ we call A and B are independent.
Why not use the intuitive deduction ?
Since this form of definition reveal the reciprocal role for A and B and apply either P(A) or P(B) is 0

Independent means events are not connected, they won’t affect each other.
Example
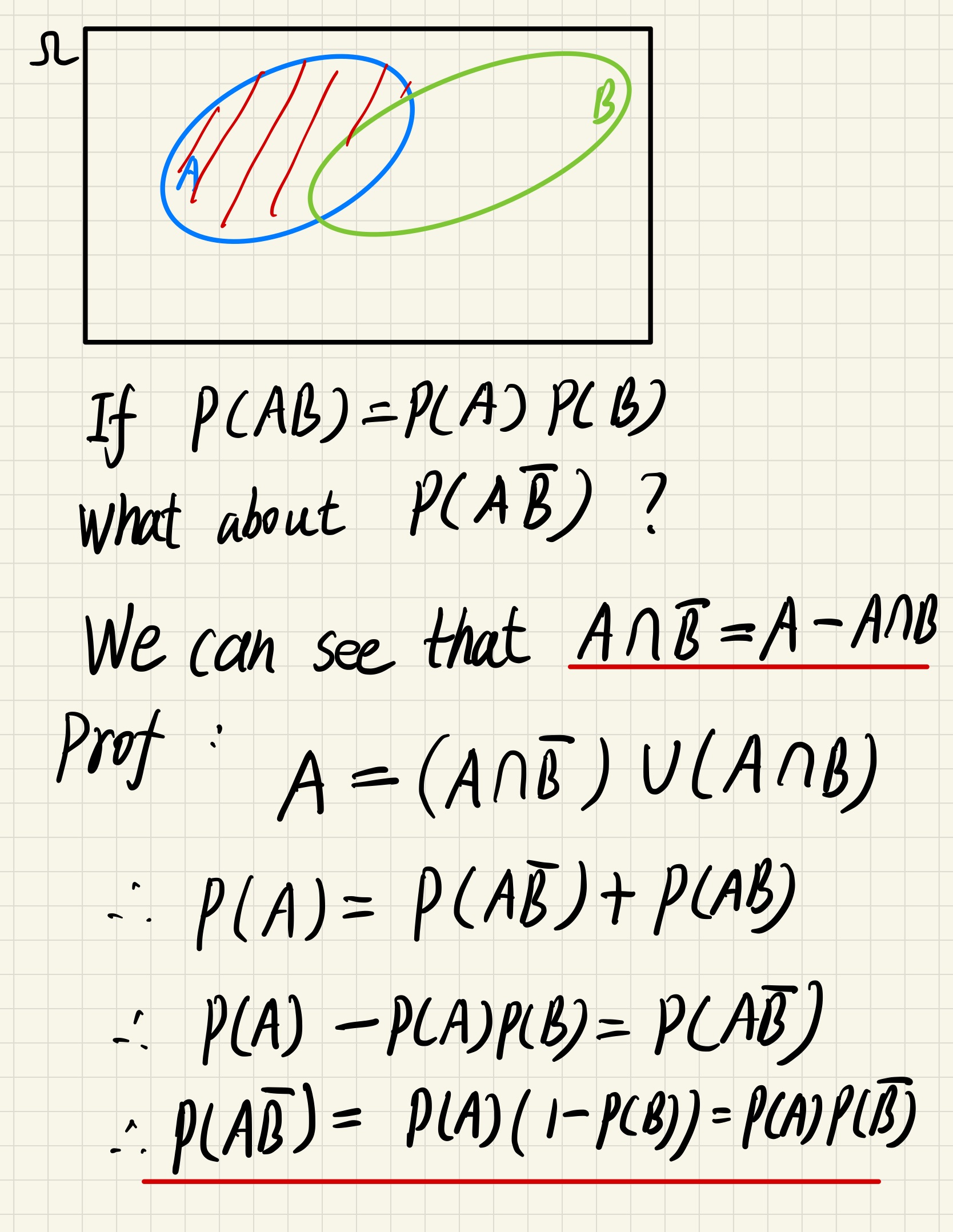
If A and B are independent, then A and $\bar{B}$ are also independent
(Since the existence of A means nothing to B, it also means nothing to B’s complement)
Conditional Independence
When some extra information is available
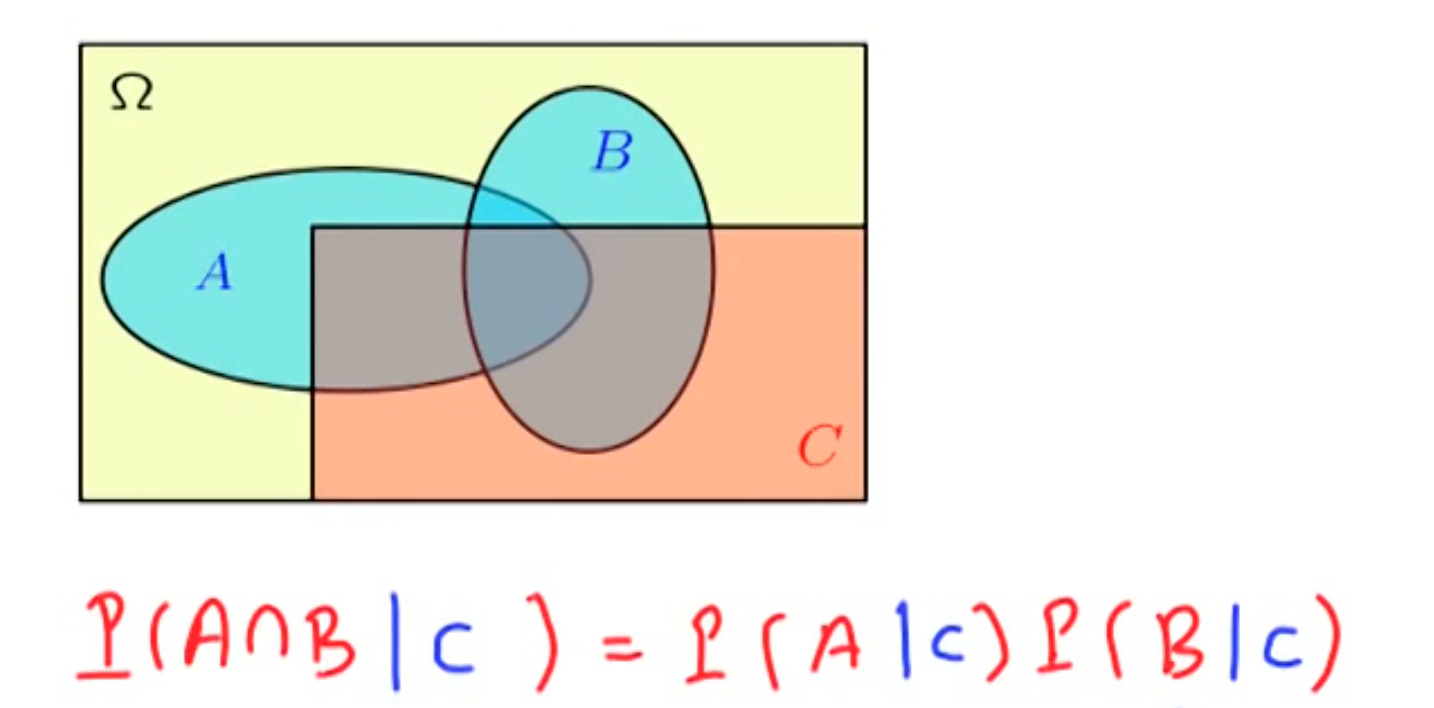
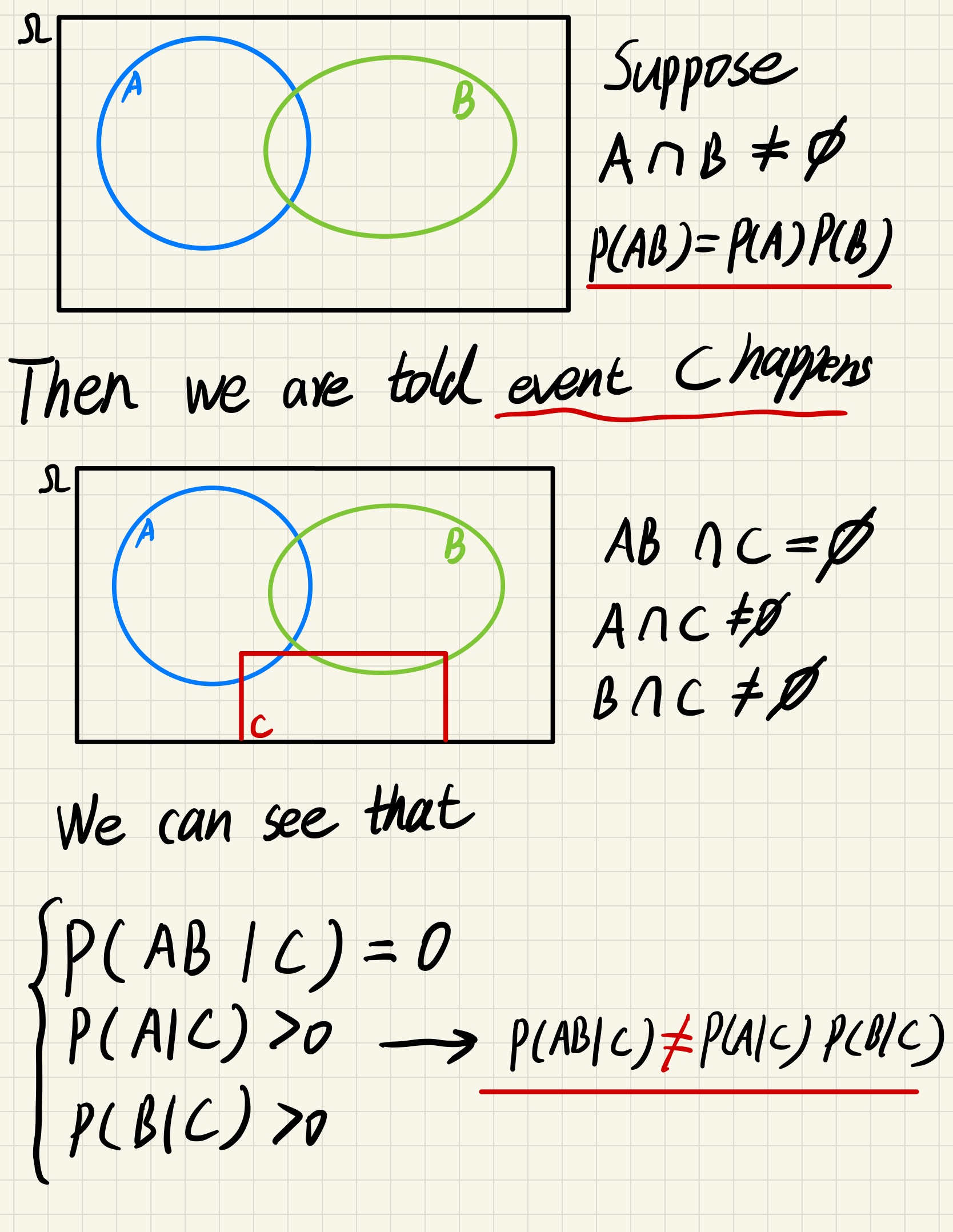
Since we don’t know wether the extra information establish a relation/dependency between existing events, we cannot say anything about independence and conditional independence
$$
\text{Independence} \not \Longleftarrow \not \Longrightarrow \text{Conditional Independence}
$$
Example

Now each toss will be affect by the previous tosses, since we can “guess” which toss we are now dealing with from previous results.
Independent collection of events
What if we have a bunch of events, and we want to say they are all independent ?
Information of some of the events does not change probabilities related to the remaining events

Notices that : mutually independent set of events is (by definition) pairwise independent; but the converse is not necessarily true.
Example

Although H1 and H2 independently doesn’t provide any useful information for C, when they combined, we know that C must happen, so the combination of them gives information about C
So pairwise independence doesn’t mean mutual independent