Derived Distribution
Compose one or more simple random variables to get more complicated r.v. (This is how we go from simple model to complicated model) ($f(X)$)
Discrete
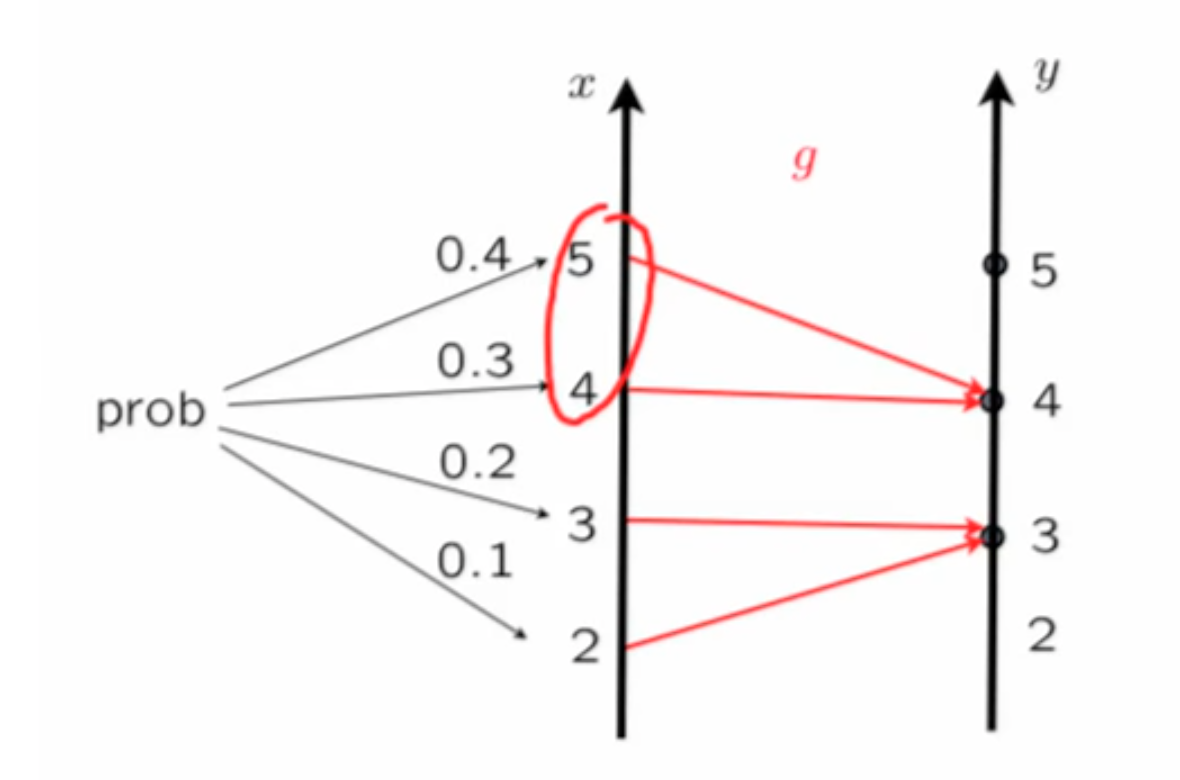
Obvious formula
$$
P_Y(y) = P(Y=y) = \sum_{\text{all x if g(x)=y}} P_X(x)
$$
$$
P_Y(4) = P_X(5)+P_X(4) = 0.4 + 0.3 = 0.7
$$
Linear Example
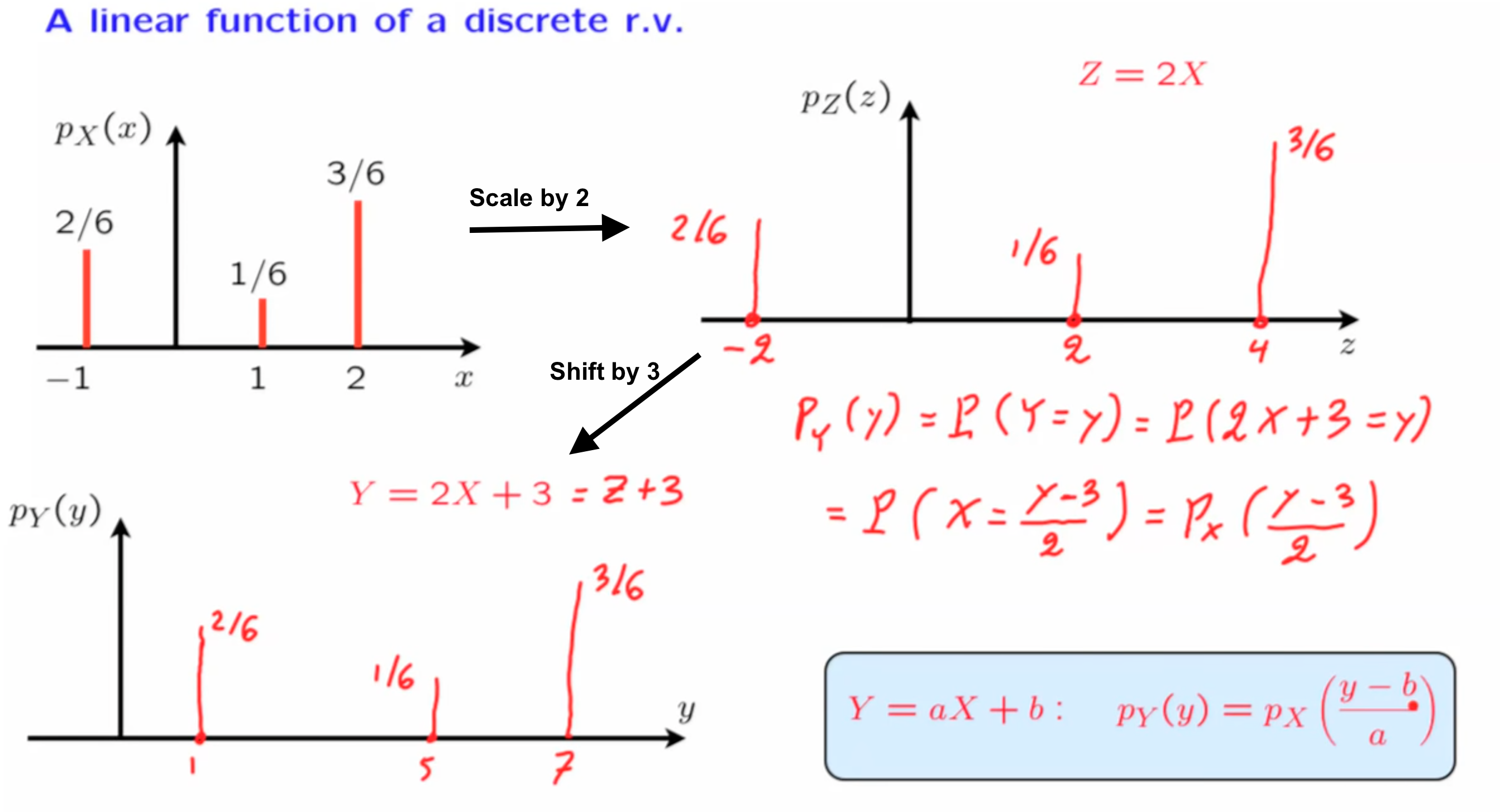
The probability doesn’t change at all, it is just a remapping
Continuous
For linear functions, it is just a similar story
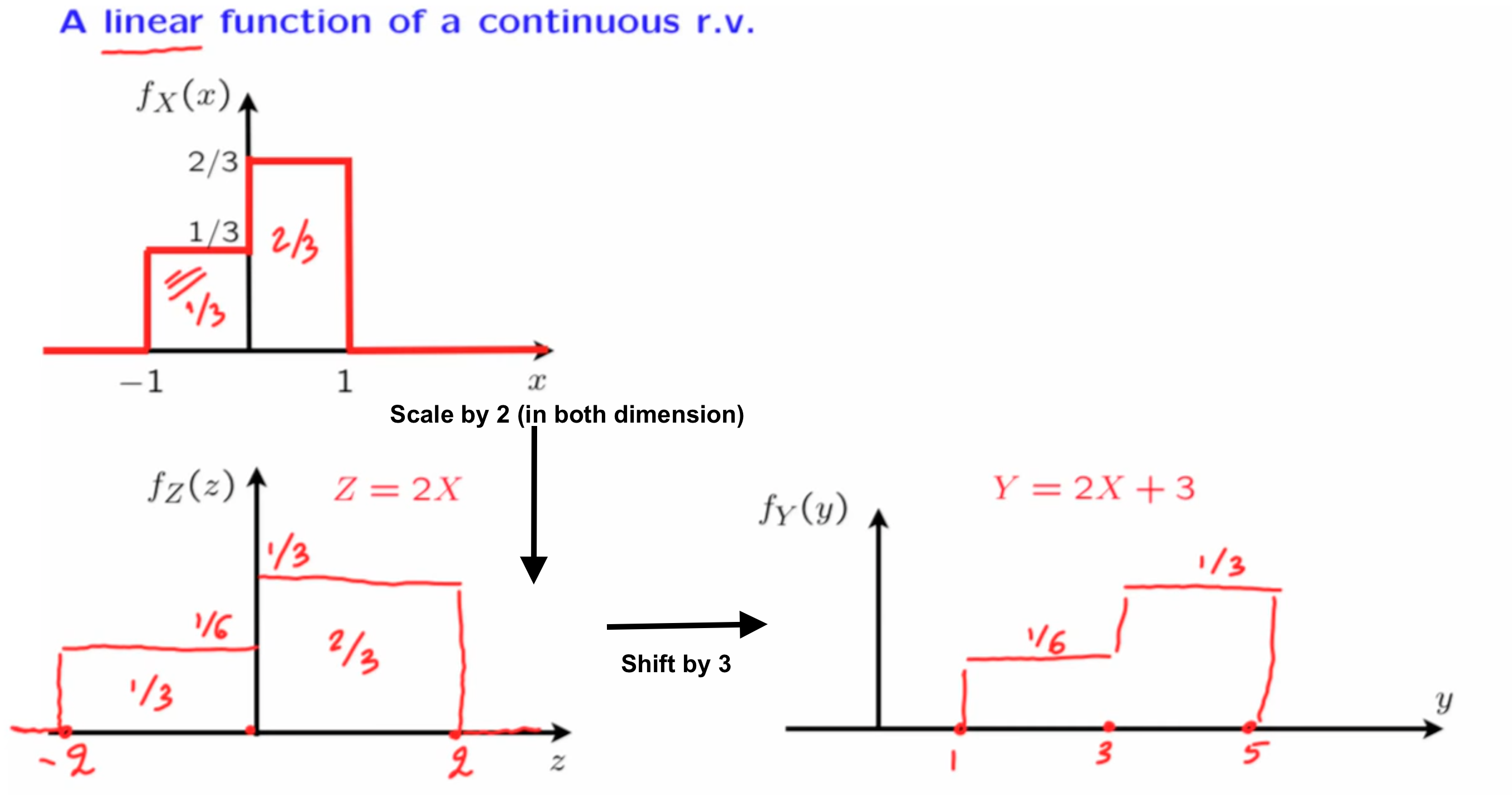
$$
Y = aX+b
$$
$$
f_Y(y) = \frac{1}{|a|}f_X(\frac{y-b}{a})
$$
Deduction

Application
we can use this formula to see that linear function applied on a normal distribution still gives a normal distribution
$$
if X \sim N(\mu , \sigma^2 ) , Y = aX+b (a\ne 0)
$$
$$
then , Y \sim N(a\mu +b , \sigma^2a^2)
$$
General/Systematic way to find any function applied on a known X
Find $F_Y(y) = P(g(X) \le y)$
Take derivative $f_Y(y) = \frac{dF_Y(y)}{dy}$