Sum of two independent r.v. and Covariance & Correlation
Sum of two independent r.v.

Example : sum of finite normal distributed r.v. is still normal distributed r.v.

Covariance
how independent r.v. related
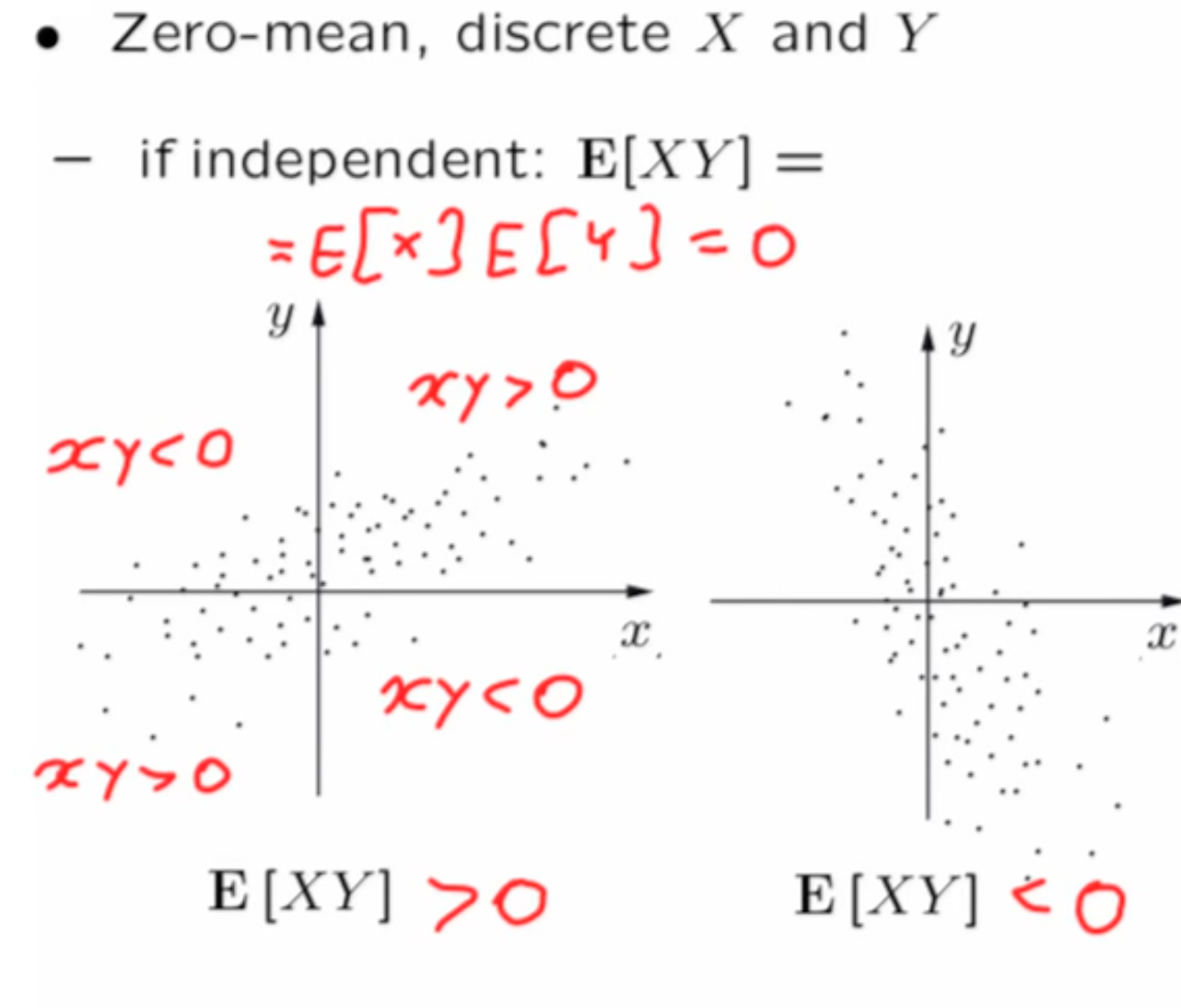
In picture 1 , When $X > 0$ , $Y$ also tend to be $> 0$, When $X < 0 $ , $Y$ tend to be $< 0$
Definition
$$
cov(X,Y) = E[(X-E[X]) (Y-E[Y])]
$$
covariance indicate how much the two r.v. are related(grow in the same direction)
$$
independent \implies Cov(X,Y) = 0
$$
$$
Cov(X,Y) \not \implies independent
$$
Property
$$
Cov(X,Y) = E[(X-E[X]) (Y-E[Y])]
$$
using linearity
$$
=E[XY]-E[XE[Y]]-E[E[X]Y]+E[X][Y]
$$
extract constant
$$
=E[XY]-E[Y]E[X]-E[Y]E[X]+E[X]E[Y]
$$
$$
\therefore Cov(X,Y) = E[XY]-E[X]E[Y]
$$
$$
Cov(aX+b,Y)=aCov(X,Y)
$$
Revisit Variance
$$
var(X_1+X_2), \text{for dependent} X_1,X_2
$$
$$
var(X_1 + X_2) = E[(X_1+X_2-E[X_1 + X_2])^2]
$$
By linearity
$$
E[(X_1+X_2-E[X_1 + X_2])^2] = E[(X_1-E[X_1] + X_2 - E[X_2])^2]
$$
$$
= var(X_1)+var(X_2)+2Cov(X,Y)
$$
Correlation Coefficient
dimensionless version of covariance
We need a way to quantify how much are two r.v. are related or not
Standard Deviation
square root of variance
$$
\sigma_X = \sqrt{var(X)}
$$
Definition
$$
\rho(X,Y) = E[\frac{X-E[X]}{\sigma_X}\frac{Y-E[Y]}{\sigma_Y}]=\frac{Cov(X,Y)}{\sigma_X \sigma_Y}
$$
Property
$-1 \le \rho \le 1$
$\rho(X,X) = 1 , \rho(X,-X) = -1$
$|\rho(X,Y)|=1 \iff X-E[X] = C(Y-E[Y])$ C is constant
$\rho(aX+b,Y) = sign(a) \times \rho(X,Y)$ when doing linear transformation, how much the two r.v. are related will not change, only the sign changes
Interpretation
Correlation coefficient does NOT mean the two r.v. influence each other. It often reflect that there is a underlying, common, hidden factor influence both the two r.v.
For example, let X be a person’s musical ability and Y be the person’s math ability. $\rho(X,Y)$ is high doesn’t mean that you study math hard will also make you a good musician, it indicate that musical ability and math ability might both controlled by the same area of a person’s mind.