Web3

TechBasic

Three key components

  • Cryptographic hash function

  • Asymmetric cryptograph(Digital Signature)

  • Consensus algorithm

Birthday Problem

How many people do you need to have two of them share the birthday ?

  1. Consider the counterpart : $\overline{P(A)}$, how can I find people that they do not share birthday ?

  2. The probability that $\overline{P(A)}$

$$
\overline{P(A)} = 1\cdot (1-\frac{1}{365}) \cdot (1 - \frac{2}{365}) \dots (1- \frac{n-1}{365})
$$

$$
= \frac{364}{365} \cdot \frac{363}{365} \dots \frac{364-n+1}{365}
$$

$$
= \frac{365!}{365^n (365-n)!}
$$

  1. Get the result

$$
P(A) = 1- \overline{P(A)} = 1 - \frac{365!}{365^n (365-n)!}
$$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
from math import factorial

def f(n):
    return 1 - factorial(365) / (365**n * factorial(365-n))
for n in range(1,30):
    print(n,"->",f(n))
"""
1 -> 0.0
2 -> 0.002739726027397249
3 -> 0.008204165884781345
4 -> 0.016355912466550326
5 -> 0.02713557369979358
6 -> 0.040462483649111536
7 -> 0.056235703095975365
8 -> 0.07433529235166902
9 -> 0.09462383388916673
10 -> 0.11694817771107768
11 -> 0.141141378321733
12 -> 0.16702478883806438
13 -> 0.19441027523242937
14 -> 0.223102512004973
15 -> 0.25290131976368635
16 -> 0.2836040052528499
17 -> 0.31500766529656066
18 -> 0.34691141787178936
19 -> 0.37911852603153673
20 -> 0.41143838358057994
21 -> 0.4436883351652058
22 -> 0.4756953076625501
23 -> 0.5072972343239854
24 -> 0.5383442579145288
25 -> 0.5686997039694639
26 -> 0.598240820135939
27 -> 0.626859282263242
28 -> 0.6544614723423994
29 -> 0.680968537477777
"""

So that we can see if we want to find a collision in a space of 365, it only takes 23 times to have a 50% success rate

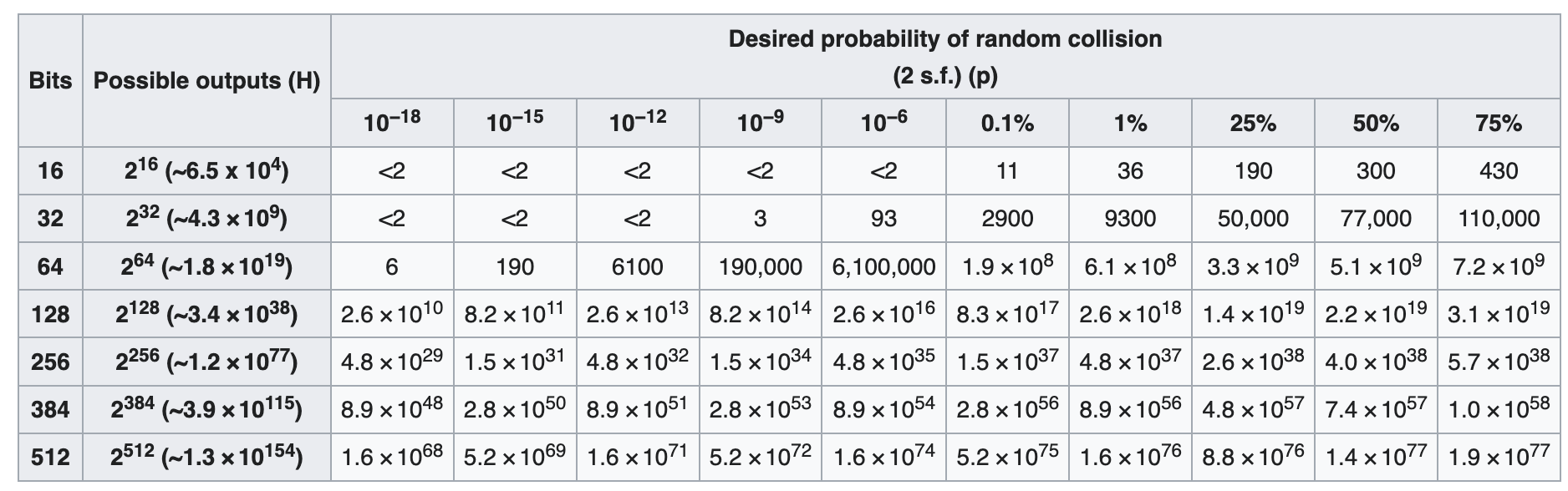
  1. Then we take this to hash algorithms, if a hash output with length 16 bits, that is space of 2**16 = 65536
1
2
3
4
f = lambda n : 1 - factorial(65536) / (65536**n * factorial(65536-n))
print(f(1000))
# 0.9995290743136814
# almost certainly a collision in 1000 times
  1. Let’s see it in practical, assume an extreme simple algorithm Pearson hashing, with output of 16 bits
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
from math import factorial

def f(base , n):
    return 1 - factorial(base) / (base**n * factorial(base-n))

def Hash(input_bytes):
    blocks = [0b00000000 , 0b11111111]
    for i,b in enumerate(input_bytes):
        blocks[i%2] ^= b
    if len(input_bytes) % 2 != 0:
        blocks[1] ^= blocks[0]
    return int.from_bytes(bytes(blocks), 'big')

from random import randbytes ,randint

class Input():
    def __init__(self) -> None:
        self.content = randbytes(randint(1,100))
        self.Hash = Hash(self.content)

    def get_Hash(self):
        return self.Hash

    def get_Content(self):
        return self.content

tests = [Input() for i in range(500)]
testss = tests
for i,t in enumerate(testss):
    for j,test in enumerate(tests[i+1:]):
        if test.get_Hash() == t.get_Hash():
            print("collision!")
            print(t.get_Content() , "\t->" , t.get_Hash())
            print(test.get_Content() , "\t->" , test.get_Hash())

"""
collision!
b"\xa1'\x0c\xf2\x1aAs\xeb~@E\x94\x80"     -> 32555
b'\x95\xf3\x02\xf9\xee\xa6^\x9b\x7fp@\x06\x91\xd5\t\xc4\xa8\xc2I\x1b\xc2\x81\xcc\x89\xe8\xbf\xcfa\xd7\x007\x90\x0e\x0b\xe5\x16b.\xdd\x9d\xc03j\xbe6Z\x17A\x1d\x16\x0b\xc2\xf0(\xca\x17\x01\xff\x1d\xb6{[\xeb\xdc\x0b\x15\x98\xd3;\xc0'     -> 32555
collision!
b'Vib\x9c\x1c\\\xddX\x18\xc2\xa9kJ\x08\x94\x8d\xdc\xacc=\x1dp\xc5\xe2\x8a\x1dI\xab\x8e@\xd7\xff\xa9UZ\xe3r\x83\xa1\x81{\xd6w\xc1\xa5\xa1\xf1hq\x1f0\xd8\xc2\xca\xf5\xa5\x17j\x81T\x89\xe3\xa3\x81\xcdK\xdc\xd1<\x00\xdc\xf6'     -> 9434
b'24\xea5r9\x03\x04\xdf\xdf3o\x9d\xf0\xe8\xaa\xd5\xd7\xe3\xa7\xea\x02\xc4\x7f\x0e\x1b#|\xd1\xd8r\x19\x1f\xe6\x83\x9a\x1e'     -> 9434
"""

So you can see how insecure the 16 bits space can be !

probability

Review of Digital Signature

RSA version

  1. RSA key generation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
def generate_random_prime():
    pass

def choose_coprime(phi):
    e = choose_prime(2,phi)
    while gcd(e,phi) != 1:
        e = choose_prime(2,phi)
    return e

def egcd(a, b):
    if a == 0:
        return (b, 0, 1)
    else:
        g, y, x = egcd(b % a, a)
        return (g, x - (b // a) * y, y)

def modinv(a, m):
    g, x, y = egcd(a, m)
    if g != 1:
        raise Exception('modular inverse does not exist')
    else:
        return x % m

def lcm(a,b):
    from math import gcd
    return a*b // gcd(a,b)

# p , q = generate_random_prime() , generate_random_prime()
p = 11
q = 17
n = p * q # 35 , len(n.to_bits()) = key length
phi = lcm((p-1),(q-1))
print(f"{phi=}") # phi = 80
# e = choose_coprime(phi) # assume we choose 29
e = 29
# d = get_modulo_inverse(e,n)
d = modinv( e, phi)
print(f"{d=}") # d = 69
public_key = (e, n)
private_key = (d , n)
  1. sign a message (encrypt with private key)
1
2
3
4
5
6
7
message = 78
def sign(message, private_key):
    d, n = private_key
    return pow( message , d , n)
signature = sign(message , private_key)
print(f"{message=},{signature=}")
# message=78,signature=23
  1. verify the signature (decrypt with public key)
1
2
3
4
5
6
7
8
9
def verify( message , signature , pub_key):
    e,n = pub_key
    return message == pow(signature , e , n)
print(verify(message , signature , public_key))
print(verify(message , sign(message, (71,n)) , public_key))
"""
True
False
"""

ECC version

if you forget about the ECC, see ECC | rubbishbin for a quick review

  1. first we need to choose the curve, bitcoin use a simple but secure curve Secp256k1, it is both secure and efficient!

    $$
    Secp256k1 : y^2 = x^3 + 7 \mod (2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 -2^6 - 2^4 - 1)
    $$

    $$
    y^2 = x^3 + ax + b \mod p, (a=0,b=7,p=(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 -2^6 - 2^4 - 1))
    $$

The generator $G$ is chosen as : see page 9 from secg

  1. Key generation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import secrets
from tinyec import registry

curve = registry.get_curve("secp256k1")

private_key = secrets.randbelow(curve.field.n)
public_key = private_key * curve.g
print(f"{private_key=}")
print(f"{public_key=}")
print(f"{curve.g=}")
"""
private_key=109345410075939956383942568843642383439719631842514450186459820386149732481155
public_key=(88923222097830077897519548732571256441526545195933396525561648144490962569413, 15010468063349613947206946585370646652800128032741145332997213280241231792495) on "secp256k1" => y^2 = x^3 + 0x + 7 (mod 115792089237316195423570985008687907853269984665640564039457584007908834671663)
curve.g=(55066263022277343669578718895168534326250603453777594175500187360389116729240, 32670510020758816978083085130507043184471273380659243275938904335757337482424) on "secp256k1" => y^2 = x^3 + 0x + 7 (mod 115792089237316195423570985008687907853269984665640564039457584007908834671663)
"""

(public key can be compressed to 257 bits, 256 for x coordinate, 1 bit indicate it is the upper point or lower point)

  1. sign the message
1
2
3
4
5
6
7
8
9
10
message = 12345
def sign(m , pk):
    secure_random_number_k = secrets.randbelow(curve.field.n)
    random_point = secure_random_number_k * curve.g
    rp_x_coordinate = random_point.x
    # encode pk and rpx into proof, prove that the signer really know the pk
    # and it is hard to recover pk from proof due to ECDL problem
    proof = ( pow(secure_random_number_k , -1 , curve.field.n) * (m + rp_x_coordinate * pk)  ) % curve.field.n
    return rp_x_coordinate , proof
signature = sign(message , private_key)
  1. verify the message

since ECDS based on ElGamal signature scheme, it can recover the public key from the signature !!!

Public key recovery from signature

1
2
3
4
5
6
def verify( m , signature , public_key):
    rpx , proof = signature
    proof_inverse = pow(proof , -1 , curve.field.n)
    rp = (m * proof_inverse) * curve.g + (rpx * proof_inverse) * public_key
    return rp.x == rpx
print(verify(message , signature , public_key))

What is an address?

It is a hashed public key

1
private_key --EC operation--> public_key --SHA256+RIPEMD160--> hashed_pk --base58--> text address

Core of crypto or any cybersecurity stuff : asymmetry

In digital world, we need asymmetry to establish security. If there is something easy for the defender/normal user to do, but hard for the attacker, then we call this thing a ‘secure technique’.

Examples

RSA

  • For user, it is easy to compute $p\times q = n$, given $p,q$

  • For attacker, it is hard to compute $p,q$ given $n$

Hash

  • For user, it is easy to compute $H(m)=h$,given $H,m$

  • For attacker, it is hard to find $m$, given $H,h$

Baby mining program

hard to find, easy to verify

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import bitstring as bs
from hashlib import sha256
import binascii

hashf = sha256
l = 20

service_name = bs.BitArray(hex = binascii.hexlify('BTC example'.encode('ascii')).decode('ascii'))

def MINT( s_name : bs.BitArray  , b : int) -> tuple:
    attempt = bs.BitArray( int = 0 , length= 8)
    while bs.BitArray( hex = binascii.hexlify(hashf((s_name + attempt).bytes).digest()).decode('ascii')) .bin[:b] != bs.BitArray(bin = '0' * 256).bin[:b]:
        if attempt.all(1):
            attempt = bs.BitArray(int = 0 , length = attempt.len + 8)
        else:
            attempt.uint += 1
        print("trying : {}, len {}".format(attempt.uint , attempt.len))

    return s_name , attempt

s , a = MINT(service_name , l) 
print( '0x'+s.hex , "+" , '0x'+a.hex , "=" , '0x'+(s+a).hex , "hashed to -> 0b" , bs.BitArray(hex = binascii.hexlify( hashf((s + a).bytes).digest() ).decode('ascii') ).bin )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
...
trying : 991101, len 24
trying : 991102, len 24
trying : 991103, len 24
trying : 991104, len 24
trying : 991105, len 24
trying : 991106, len 24
trying : 991107, len 24
trying : 991108, len 24
trying : 991109, len 24
trying : 991110, len 24
trying : 991111, len 24
trying : 991112, len 24
trying : 991113, len 24
trying : 991114, len 24
trying : 991115, len 24
trying : 991116, len 24
trying : 991117, len 24
trying : 991118, len 24
trying : 991119, len 24
trying : 991120, len 24
trying : 991121, len 24
trying : 991122, len 24
trying : 991123, len 24
trying : 991124, len 24
trying : 991125, len 24
trying : 991126, len 24
trying : 991127, len 24
0x425443206578616d706c65 + 0x0f1f97 = 0x425443206578616d706c650f1f97 hashed to -> 0b 0000000000000000000000011001110000110001001101100010000010100011010111101001000011001111110001110001010011111101101011011100110000010010011011111110010111001100011000011000101100101111100101110001101001010101011100001110001110111100110100000101110111100100
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import bitstring as bs
from hashlib import sha256
import binascii

service = '425443206578616d706c65'
proof_of_work = '0f1f97'

s = bs.BitArray(hex = service)
p = bs.BitArray(hex = proof_of_work)
hashf = sha256

res =  bs.BitArray( hex = binascii.hexlify(hashf((s + p).bytes).digest()).decode('ascii') ).bin 

print(res)
print( res[:20] , "all zeros")<script type="text/javascript" id="MathJax-script" async
  src="https://cdn.jsdelivr.net/npm/mathjax@3/es5/tex-mml-chtml.js">
</script>